再看LDA主题模型
之前学习文本挖掘时已经写过一篇关于主题模型的博客《文本建模之Unigram Model,PLSA与LDA》,前几天小组讨论主题模型时,又重新理解了一遍LDA,有了更深刻的认识,特记录一下。
1、Unigram Model
Unigram model是最简单的文本模型,其直接将文本的生成过程看作是从一个词汇表中重复取词的过程。因此只要知道每个词的产生概率,就能计算出一篇文档的产生概率。假设一篇文档由 N N N个词 w 1 , w 2 , … , w n w_1,w_2,\dots,w_n w1,w2,…,wn组成,如下图所示:

这 N N N个词必定来自于一个词汇表 v 1 , v 2 , ⋯ , v V v_1,v_2,\cdots,v_V v1,v2,⋯,vV,其中 V V V是词汇表大小, v i v_i vi是词汇表中某一个词,上图中红、黄、蓝、绿代表文档中该词所对应的词汇表中词。文档中每个词的产生相互独立(不考虑词产生过程中的相互影响),因此在知道词汇表中每个词的产生概率 p ⃗ = ( p v 1 , p v 2 , … , p v V ) \vec{p}=(p_{v_1},p_{v_2},\dots,p_{v_V}) p=(pv1,pv2,…,pvV),和词汇表中每个词的出现次数 n ⃗ = ( n v 1 , n v 2 , … , n v V ) \vec{n}=(n_{v_1},n_{v_2},\dots,n_{v_V}) n=(nv1,nv2,…,nvV),同时 n v 1 + n v 2 + ⋯ + n v V = N n_{v_1}+n_{v_2}+\dots+n_{v_V}=N nv1+nv2+⋯+nvV=N, n ⃗ \vec{n} n的发生概率满足多项分布:
p ( n ⃗ ) = M u l t i ( n ⃗ ∣ p ⃗ , N ) = ( N n ⃗ ) ∏ i = 1 V p v i n v i p(\vec{n})=Multi(\vec{n}|\vec{p},N)=\begin{pmatrix} N \\ \vec{n} \end{pmatrix}\prod_{i=1}^Vp_{v_i}^{n_{v_i}} p(n)=Multi(n∣p,N)=(Nn)i=1∏Vpvinvi
一篇文档相当于词汇表中 V V V各词 n n n次取值实验中的一种,因此一篇文档的产生概率可以写成:
p ( w ⃗ ) = ∏ i = 1 V p v i n v i p(\vec{w})=\prod_{i=1}^Vp_{v_i}^{n_{v_i}} p(w)=i=1∏Vpvinvi
语料中 M M M篇文档的生成过程相互独立,所以语料的产生概率为:
p ( W ) = ∏ m = 1 M ∏ i = 1 V p v i n m v i = ∏ i = 1 p v i n v i p(W)=\prod_{m=1}^M\prod_{i=1}^Vp_{v_i}^{n_{mv_i}}=\prod_{i=1}p_{v_i}^{n_{v_i}} p(W)=m=1∏Mi=1∏Vpvinmvi=i=1∏pvinvi
此处, n m v i n_{mv_i} nmvi表示词汇表中词 v i v_i vi在第 m m m篇文档中的出现次数, n v i n_{v_i} nvi表示 v i v_i vi在整个语料库中的出现次数。现在,只剩下最后一个问题,怎么通过观测到的语料去估计词汇表中每个词的产生概率 p ⃗ \vec{p} p,按照频率学派和贝叶斯学派的观点,存在两种计算方法。
频率学派
频率学派认为,词汇表中每个词的产生概率 p ⃗ \vec{p} p虽然未知,但是其取值是固定的,是取值空间中的一个定值。 可以采用最大似然估计,于是参数 p ⃗ \vec{p} p的估计值是
p ^ v i = n v i N \hat{p}_{v_i}=\frac{n_{v_i}}{N} p^vi=Nnvi
其图模型是

图中方框表示重复此过程,灰色圆圈的w表示可观测变量,N表示一篇文档中包含N个单词,M表示生成M篇文档。
贝叶斯学派
贝叶斯学派认为,词汇表中每个词的产生概率 p ⃗ \vec{p} p不仅未知,且其取值也未定,取值空间中的每种情况都有可能取到,也就是说,分布 p ⃗ \vec{p} p也是从一个概率分布中取出来的,我们称这个概率分布为 p ⃗ \vec{p} p的先验分布。 因为每一个分布 p ⃗ \vec{p} p都有可能产生我们的语料,我们不知道语料究竟是由哪一个 p ⃗ \vec{p} p产生。假设 p ⃗ \vec{p} p被选中的概率为 p ( p ⃗ ) p(\vec{p}) p(p),那么此时语料的产生概率为:
p ( W ) = ∫ p ( W ∣ p ⃗ ) p ( p ⃗ ) d p ⃗ p(W)=\int p(W|\vec{p})p(\vec{p})d\vec{p} p(W)=∫p(W∣p)p(p)dp
上面的推导中,我们已经知道 p ( n ⃗ ) p(\vec{n}) p(n)符合多项分布, p ( W ) p(W) p(W)是 n ⃗ \vec{n} n的一种情况,因此也可以近似认为 p ( W ) p(W) p(W)符合多项分布,所以先验分布 p ( p ⃗ ) p(\vec{p}) p(p)的一个较比好的选择是多项分布的共轭先验分布,即Dirichlet分布 D i r ( p ⃗ ∣ α ⃗ ) Dir(\vec{p}|\vec{\alpha}) Dir(p∣α)。此时,语料的产生概率为:
p ( W ∣ α ⃗ ) = ∫ p ( W ∣ p ⃗ ) p ( p ⃗ ∣ α ⃗ ) d p ⃗ = ∫ ∏ i = 1 V p v i n v i D i r ( p ⃗ ∣ α ⃗ ) d p ⃗ = ∫ ∏ i = 1 V p v i n v i 1 Δ ( α ⃗ ) ∏ i = 1 V p v i α i − 1 d p ⃗ = 1 Δ ( α ⃗ ) ∫ ∏ i = 1 V p v i α i + n v i − 1 d p ⃗ = Δ ( n ⃗ + α ⃗ ) Δ ( α ⃗ ) \begin{aligned} p(W|\vec{\alpha}) &= \int p(W|\vec{p})p(\vec{p}|\vec{\alpha})d\vec{p}\\ &= \int\prod_{i=1}^Vp_{v_i}^{n_{v_i}}Dir(\vec{p}|\vec{\alpha})d\vec{p} \\ &= \int\prod_{i=1}^Vp_{v_i}^{n_{v_i}}\frac{1}{\Delta(\vec{\alpha})}\prod_{i=1}^Vp_{v_i}^{\alpha_i-1}d\vec{p} \\ &= \frac{1}{\Delta(\vec{\alpha})}\int\prod_{i=1}^Vp_{v_i}^{\alpha_i+n_{v_i}-1}d\vec{p} \\ &= \frac{\Delta(\vec{n}+\vec{\alpha})}{\Delta(\vec{\alpha})} \end{aligned} p(W∣α)=∫p(W∣p)p(p∣α)dp=∫i=1∏VpvinviDir(p∣α)dp=∫i=1∏VpvinviΔ(α)1i=1∏Vpviαi−1dp=Δ(α)1∫i=1∏Vpviαi+nvi−1dp=Δ(α)Δ(n+α)
因为Dirichlet先验+多项分布的数据 → \rightarrow →后验分布为Dirichlet分布,所以分布 p ⃗ \vec{p} p的后验分布为 D i r ( p ⃗ ∣ n ⃗ + α ⃗ ) Dir(\vec{p}|\vec{n}+\vec{\alpha}) Dir(p∣n+α)
p ( p ⃗ ∣ W , α ⃗ ) = D i r ( p ⃗ ∣ n ⃗ + α ⃗ ) = 1 Δ ( n ⃗ + α ⃗ ) ∏ i = 1 V p v i n v i + α i − 1 d p ⃗ p(\vec{p}|W,\vec{\alpha})=Dir(\vec{p}|\vec{n}+\vec{\alpha})=\frac{1}{\Delta(\vec{n}+\vec{\alpha})}\prod_{i=1}^Vp_{v_i}^{n_{v_i}+\alpha_i-1}d\vec{p} p(p∣W,α)=Dir(p∣n+α)=Δ(n+α)1i=1∏Vpvinvi+αi−1dp
因此可以用 p ⃗ \vec{p} p的后验分布的均值作为 p ⃗ \vec{p} p的估计值:
p ^ v i = n v i + α i ∑ k = 1 V ( n v k + α k ) \hat{p}_{v_i}=\frac{n_{v_i}+\alpha_i}{\sum_{k=1}^V(n_{v_k}+\alpha_k)} p^vi=∑k=1V(nvk+αk)nvi+αi
贝叶斯学派下,对应的图模型如下:

主题模型(topic model)
Unigram Model将一篇文档的生成过程简单地看作是从词袋中不断取词的过程显然于人类在写文章时遣词造句的过程存在较大差距。通常,我们在写文章时,首先会确定文章所包含的主题,然后根据主题选择相应的单词。基于以上思想,我们可以将词的产生过程拆分为两步:(1)产生位置 i i i的主题 z i z_i zi;(2)从主题对应的词分布下产生词 w i w_i wi。譬如一篇关于自然语言处理的文章,可能包含40%的语言学,30%的概率统计,20%的计算机,10%的其他主题,我们能够观察到的是文章中的词,但这个词是在哪一个主题下产生的并不清楚,每一个主题对应的词分布都有可能产生这个词,只是概率大小不一样:

因此,第 m m m篇文档 d m d_m dm中词 v i v_i vi的产生概率为
p ( v i ∣ d m ) = ∑ k = 1 K p ( v i ∣ z k ) p ( z k ∣ d m ) p(v_i|d_m)=\sum_{k=1}^Kp(v_i|z_k)p(z_k|d_m) p(vi∣dm)=k=1∑Kp(vi∣zk)p(zk∣dm)
其中 z ⃗ = ( z 1 , z 2 , … , z k ) \vec{z}=(z_1,z_2,\dots,z_k) z=(z1,z2,…,zk)表示一篇文档中每个topic的概率,因此第 m m m篇文档 d m d_m dm的产生概率为
p ( w ⃗ ∣ d m ) = ∏ i = 1 V p ( v i ∣ d m ) n ( v i , d m ) p(\vec{w}|d_m)=\prod_{i=1}^Vp(v_i|d_m)^{n(v_i,d_m)} p(w∣dm)=i=1∏Vp(vi∣dm)n(vi,dm)
其中 n ( v i , d m ) n(v_i,d_m) n(vi,dm)表示文档 d m d_m dm中词 v i v_i vi的出现次数。整个语料的产生概率为
p ( W ) = ∏ m = 1 M p ( d m ) p ( w ⃗ ∣ d m ) = ∏ m = 1 M p ( d m ) ∏ i = 1 V p ( v i ∣ d m ) n ( v i , d m ) = ∏ m = 1 M p ( d m ) ∏ i = 1 V ∑ k = 1 K ( p ( v i ∣ z k ) p ( z k ∣ d m ) ) n ( v i , d m ) \begin{aligned} p(W) &=\prod_{m=1}^Mp(d_m)p(\vec{w}|d_m)\\ &=\prod_{m=1}^Mp(d_m)\prod_{i=1}^Vp(v_i|d_m)^{n(v_i,d_m)}\\ &=\prod_{m=1}^Mp(d_m)\prod_{i=1}^V\sum_{k=1}^K\Big(p(v_i|z_k)p(z_k|d_m)\Big)^{n(v_i,d_m)} \end{aligned} p(W)=m=1∏Mp(dm)p(w∣dm)=m=1∏Mp(dm)i=1∏Vp(vi∣dm)n(vi,dm)=m=1∏Mp(dm)i=1∏Vk=1∑K(p(vi∣zk)p(zk∣dm))n(vi,dm)
上式中, p ( d m ) p(d_m) p(dm)和 n ( v i , d m ) n(v_i,d_m) n(vi,dm)是已知的, p ( v i ∣ z k ) p(v_i|z_k) p(vi∣zk)和 p ( z k ∣ d m ) p(z_k|d_m) p(zk∣dm)是未知的,对于其取值同样存在频率学派和贝叶斯学派两种观点。
PLSA
PLSA(Probabilistic Latent Semantic Analysis)由Hofmann在1990年提出,PLSA属于频率学派的观点,即 p ( v i ∣ z k ) p(v_i|z_k) p(vi∣zk)和 p ( z k ∣ d m ) p(z_k|d_m) p(zk∣dm)的取值未知,但是取值空间的某一个定值, 可以采用最大似然估计求解:
log p ( W ) = log ( ∏ m = 1 M p ( d m ) ∏ i = 1 V ∑ k = 1 K ( p ( v i ∣ z k ) p ( z k ∣ d m ) ) n ( v i , d m ) ) = ∑ m = 1 M log ( p ( d m ) ∏ i = 1 V ∑ k = 1 K ( p ( v i ∣ z k ) p ( z k ∣ d m ) ) n ( v i , d m ) ) = ∑ m = 1 M ( log p ( d m ) + log ( ∏ i = 1 V ∑ k = 1 K ( p ( v i ∣ z k ) p ( z k ∣ d m ) ) n ( v i , d m ) ) ) = ∑ m = 1 M ( log p ( d m ) + ∑ i = 1 V n ( v i , d m ) log ∑ k = 1 K p ( v i ∣ z k ) p ( z k ∣ d m ) ) \begin{aligned} \log p(W) &=\log \Bigg(\prod_{m=1}^Mp(d_m)\prod_{i=1}^V\sum_{k=1}^K\Big(p(v_i|z_k)p(z_k|d_m)\Big)^{n(v_i,d_m)}\Bigg)\\ &=\sum_{m=1}^M\log\bigg(p(d_m)\prod_{i=1}^V\sum_{k=1}^K\Big(p(v_i|z_k)p(z_k|d_m)\Big)^{n(v_i,d_m)}\bigg)\\ &=\sum_{m=1}^M\Bigg(\log p(d_m)+\log\bigg(\prod_{i=1}^V\sum_{k=1}^K\Big(p(v_i|z_k)p(z_k|d_m)\Big)^{n(v_i,d_m)}\bigg)\Bigg)\\ &=\sum_{m=1}^M\Bigg(\log p(d_m)+\sum_{i=1}^V{n(v_i,d_m)}\log\sum_{k=1}^Kp(v_i|z_k)p(z_k|d_m)\Bigg) \end{aligned} logp(W)=log(m=1∏Mp(dm)i=1∏Vk=1∑K(p(vi∣zk)p(zk∣dm))n(vi,dm))=m=1∑Mlog(p(dm)i=1∏Vk=1∑K(p(vi∣zk)p(zk∣dm))n(vi,dm))=m=1∑M(logp(dm)+log(i=1∏Vk=1∑K(p(vi∣zk)p(zk∣dm))n(vi,dm)))=m=1∑M(logp(dm)+i=1∑Vn(vi,dm)logk=1∑Kp(vi∣zk)p(zk∣dm))
通过最大化这个对数似然函数就能求解出 p ( v i ∣ z k ) p(v_i|z_k) p(vi∣zk)和 p ( z k ∣ d m ) p(z_k|d_m) p(zk∣dm),对于这种含有隐变量的参数估计,可以采用EM算法。PLSA对应的图模型如下:
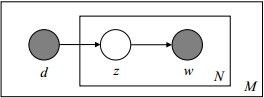
图中, d d d代表一篇文档,文档确定后其主题分布也就确定了, z z z代表主题, d d d和 w w w是可观测到变量。
LDA
PLSA认为每一篇文档的主题分布是唯一的,每个主题下的词分布也是唯一的,这显然不符合贝叶斯学派的观点,因此Blei在PLSA的基础上加入贝叶斯框架,将其改造成贝叶斯版本,提出了LDA(Latent Dirichlet Allocation)模型。即主题分布和主题下词分布都是从一个概率分布中以相应概率取出的。 因此LDA对应的图模型如下:
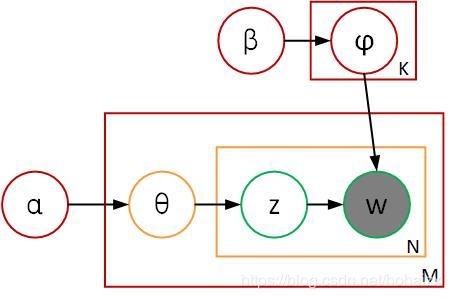
图中,红色的框表示语料级,黄色的框表示文档级,绿色的框表示单词级。 θ \theta θ是文档的主题分布, φ \varphi φ是主题下的词分布。我们说一篇文档的产生过程是:先产生位置 i i i的主题,然后根据该主题产生位置 i i i对应的词,重复这个过程 N N N次就产生了一篇文档。我们也可以换一个做法:先产生文档每个位置的主题 z 1 , z 2 , … , z n z_1,z_2,\dots,z_n z1,z2,…,zn,然后产生每个位置对应的词 w 1 , w 2 , … , w n w_1,w_2,\dots,w_n w1,w2,…,wn。 重复文档产生过程 M M M次,就产生了语料库中的 M M M篇文档。

这种做法的好处是,一次性产生一篇文档每个位置的主题后,我们可以顺势统计每个主题的出现次数 z m ⃗ = ( n 1 , m , n 2 , m , … , n k , m ) \vec{z_m}=(n_{1,m},n_{2,m},\dots,n_{k,m}) zm=(n1,m,n2,m,…,nk,m), n k , m n_{k,m} nk,m表示第 m m m篇文档中主题 k k k出现的次数,显然在给定第 m m m篇文档的主题分布 θ m ⃗ \vec{\theta_m} θm后, z m ⃗ \vec{z_m} zm符合多项分布:
p ( z m ⃗ ∣ θ m ⃗ ) = ∏ k = 1 K θ k , m n k , m p(\vec{z_m}|\vec{\theta_m})=\prod_{k=1}^K\theta_{k,m}^{n_{k,m}} p(zm∣θm)=k=1∏Kθk,mnk,m
θ k , m \theta_{k,m} θk,m表示第 m m m篇文档中主题 k k k出现概率,因为文档的主题分布是不固定的,根据主题出现次数符合多项分布,我们同样假设主题分布的分布(主题的先验分布)为Dirichlet分布,即
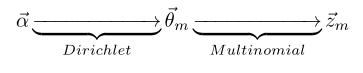
所以第 m m m篇文档的主题为 z m ⃗ \vec{z_m} zm的概率是
p ( z m ⃗ ∣ α ⃗ ) = ∫ p ( z m ⃗ ∣ θ m ⃗ ) p ( θ m ⃗ ∣ α ⃗ ) d θ m ⃗ = ∫ p ( z m ⃗ ∣ θ m ⃗ ) D i r ( θ m ⃗ ∣ α ⃗ ) d θ m ⃗ = ∫ ∏ k = 1 K θ k , m n k , m 1 Δ ( α ⃗ ) ∏ k = 1 K θ k , m α k − 1 d θ m ⃗ = 1 Δ ( α ⃗ ) ∫ ∏ k = 1 K θ k , m n k , m + α k − 1 d θ m ⃗ = Δ ( z m ⃗ + α ⃗ ) Δ ( α ⃗ ) \begin{aligned} p(\vec{z_m}|\vec{\alpha}) &=\int p(\vec{z_m}|\vec{\theta_m})p(\vec{\theta_m}|\vec{\alpha})d\vec{\theta_m}\\ &=\int p(\vec{z_m}|\vec{\theta_m})Dir(\vec{\theta_m}|\vec{\alpha})d\vec{\theta_m}\\ &=\int \prod_{k=1}^K\theta_{k,m}^{n_{k,m}}\frac{1}{\Delta(\vec{\alpha})}\prod_{k=1}^K\theta_{k,m}^{\alpha_{k}-1}d\vec{\theta_m}\\ &=\frac{1}{\Delta(\vec{\alpha})}\int\prod_{k=1}^K\theta_{k,m}^{n_{k,m}+\alpha_{k}-1}d\vec{\theta_m}\\ &=\frac{\Delta(\vec{z_m}+\vec{\alpha})}{\Delta(\vec{\alpha})} \end{aligned} p(zm∣α)=∫p(zm∣θm)p(θm∣α)dθm=∫p(zm∣θm)Dir(θm∣α)dθm=∫k=1∏Kθk,mnk,mΔ(α)1k=1∏Kθk,mαk−1dθm=Δ(α)1∫k=1∏Kθk,mnk,m+αk−1dθm=Δ(α)Δ(zm+α)
因为Dirichlet先验+多项分布的数据 → \rightarrow →后验分布为Dirichlet分布,所以主题的后验分布还是Dirichlet分布
p ( θ m ⃗ ∣ z m ⃗ , α ⃗ ) = D i r ( θ m ⃗ ∣ z m ⃗ + α ⃗ ) p(\vec{\theta_m}|\vec{z_m},\vec{\alpha})=Dir(\vec{\theta_m}|\vec{z_m}+\vec{\alpha}) p(θm∣zm,α)=Dir(θm∣zm+α)
语料库中 M M M篇文档的产生过程相互独立,因此有 M M M个相互独立的Dirichlet-Multinomial分布,从而整个语料库的主题分布概率为
p ( z ⃗ ∣ α ⃗ ) = ∏ m = 1 M p ( z m ⃗ ∣ α ⃗ ) = ∏ m = 1 M Δ ( z m ⃗ + α ⃗ ) Δ ( α ⃗ ) p(\vec{z}|\vec{\alpha})=\prod_{m=1}^Mp(\vec{z_m}|\vec{\alpha})=\prod_{m=1}^M\frac{\Delta(\vec{z_m}+\vec{\alpha})}{\Delta(\vec{\alpha})} p(z∣α)=m=1∏Mp(zm∣α)=m=1∏MΔ(α)Δ(zm+α)
每篇文档每个位置的主题生成好后,就可以在相应主题下按词分布生成对应位置的词,紧接着我们可以统计出语料中每个主题下词汇表中每个词的出现次数 w k ⃗ = ( n v 1 , k , n v 2 , k , … , n v V , k ) \vec{w_k}=(n_{v_1,k},n_{v_2,k},\dots,n_{v_V,k}) wk=(nv1,k,nv2,k,…,nvV,k),如上图右边所示, n v i , k n_{v_i,k} nvi,k表示主题 k k k下词汇表中词 v i v_i vi的出现次数,显然在给定主题 k k k对应的词分布 φ k ⃗ \vec{\varphi_k} φk的情况下, w k ⃗ \vec{w_k} wk符合多项分布
p ( w k ⃗ ∣ φ k ⃗ ) = ∏ i = 1 V φ v i , k n v i , k p(\vec{w_k}|\vec{\varphi_k})=\prod_{i=1}^V\varphi_{v_i,k}^{n_{v_i,k}} p(wk∣φk)=i=1∏Vφvi,knvi,k
φ v i , k \varphi_{v_i,k} φvi,k表示主题 k k k下词汇表中词 v i v_i vi的产生概率,因为主题对应的词分布是不固定的,根据主题下词汇表中词出现次数符合多项分布,我们同样假设主题下词分布的的分布(主题下词的先验分布)为Dirichlet分布,即

所以主题 k k k下词为 w k ⃗ \vec{w_k} wk的概率是:
p ( w k ⃗ ∣ z k , β ⃗ ) = ∫ p ( w k ⃗ ∣ φ k ⃗ ) p ( φ k ⃗ ∣ β ⃗ ) d φ k ⃗ = ∫ p ( w k ⃗ ∣ φ k ⃗ ) D i r ( φ k ⃗ ∣ z k , β ⃗ ) d φ k ⃗ = ∫ ∏ i = 1 V φ v i , k n v i , k 1 Δ ( β ⃗ ) ∏ i = 1 V φ v i , k β i − 1 d φ k ⃗ = 1 Δ ( β ⃗ ) ∫ ∏ i = 1 V φ v i , k n v i , k + β i − 1 d φ k ⃗ = Δ ( w k ⃗ + β ⃗ ) Δ ( β ⃗ ) \begin{aligned} p(\vec{w_k}|z_k,\vec{\beta}) &=\int p(\vec{w_k}|\vec{\varphi_k})p(\vec{\varphi_k}|\vec{\beta})d\vec{\varphi_k}\\ &=\int p(\vec{w_k}|\vec{\varphi_k})Dir(\vec{\varphi_k}|z_k,\vec{\beta})d\vec{\varphi_k}\\ &=\int \prod_{i=1}^V\varphi_{v_i,k}^{n_{v_i,k}}\frac{1}{\Delta(\vec{\beta})}\prod_{i=1}^V\varphi_{v_i,k}^{\beta_{i}-1}d\vec{\varphi_k}\\ &=\frac{1}{\Delta(\vec{\beta})}\int\prod_{i=1}^V\varphi_{v_i,k}^{n_{v_i,k}+\beta_{i}-1}d\vec{\varphi_k}\\ &=\frac{\Delta(\vec{w_k}+\vec{\beta})}{\Delta(\vec{\beta})} \end{aligned} p(wk∣zk,β)=∫p(wk∣φk)p(φk∣β)dφk=∫p(wk∣φk)Dir(φk∣zk,β)dφk=∫i=1∏Vφvi,knvi,kΔ(β)1i=1∏Vφvi,kβi−1dφk=Δ(β)1∫i=1∏Vφvi,knvi,k+βi−1dφk=Δ(β)Δ(wk+β)
因为Dirichlet先验+多项分布的数据 → \rightarrow →后验分布为Dirichlet分布,主题下词的后验分布还是Dirichlet分布:
p ( φ k ⃗ ∣ w k ⃗ , β ⃗ ) = D i r ( φ k ⃗ ∣ w k ⃗ + β ⃗ ) p(\vec{\varphi_{k}}|\vec{w_k},\vec{\beta})=Dir(\vec{\varphi_k}|\vec{w_k}+\vec{\beta}) p(φk∣wk,β)=Dir(φk∣wk+β)
语料中 K K K个主题产生词的过程相互独立,因此有 K K K个相互独立的Dirichlet-Multinomial共轭分布,所以在给定主题分布后,整个语料的词分布概率为
p ( W ∣ z ⃗ , β ⃗ ) = ∏ k = 1 K Δ ( w k ⃗ + β ⃗ ) Δ ( β ⃗ ) p(W|\vec{z},\vec{\beta})=\prod_{k=1}^K\frac{\Delta(\vec{w_k}+\vec{\beta})}{\Delta(\vec{\beta})} p(W∣z,β)=k=1∏KΔ(β)Δ(wk+β)
所以,最终语料的主题分布为 z ⃗ \vec{z} z且词分布为 W W W的概率为
p ( W , z ⃗ ∣ α ⃗ , β ⃗ ) = p ( W ∣ z ⃗ , β ⃗ ) p ( z ⃗ ∣ α ⃗ ) = ∏ k = 1 K Δ ( w k ⃗ + β ⃗ ) Δ ( β ⃗ ) ∏ m = 1 M Δ ( z m ⃗ + α ⃗ ) Δ ( α ⃗ ) \begin{aligned} p(W,\vec{z}|\vec{\alpha},\vec{\beta}) &=p(W|\vec{z},\vec{\beta})p(\vec{z}|\vec{\alpha})\\ &=\prod_{k=1}^K\frac{\Delta(\vec{w_k}+\vec{\beta})}{\Delta(\vec{\beta})}\prod_{m=1}^M\frac{\Delta(\vec{z_m}+\vec{\alpha})}{\Delta(\vec{\alpha})} \end{aligned} p(W,z∣α,β)=p(W∣z,β)p(z∣α)=k=1∏KΔ(β)Δ(wk+β)m=1∏MΔ(α)Δ(zm+α)
有了联合分布 p ( W , z ⃗ ∣ α ⃗ , β ⃗ ) p(W,\vec{z}|\vec{\alpha},\vec{\beta}) p(W,z∣α,β),我们可以利用Gibbs Sampling对参数进行估计。联合概率 p ( W , z ⃗ ) p(W,\vec{z}) p(W,z)中 W W W是可观测变量, z ⃗ \vec{z} z是隐变量,即我们想要知道的是 p ( z ⃗ ∣ W ) p(\vec{z}|W) p(z∣W),所以我们可以对概率 p ( z ⃗ ∣ W ) p(\vec{z}|W) p(z∣W)进行Gibbs采样,Gibbs采样中最重要的是计算出 p ( z i = k ∣ z ⃗ ¬ i , W ) p(z_i=k|\vec{z}_{\neg i},W) p(zi=k∣z¬i,W)的概率,其中 i = ( m , n ) i=(m,n) i=(m,n)表示第 m m m篇文档第 n n n个词, ¬ i \neg i ¬i表示除下标 i i i外的所有其他词。
p ( z i = k ∣ z ⃗ ¬ i , W ) ∝ n k , m ¬ i + α k ∑ k = 1 K ( n k , m ¬ i + α k ) ⋅ n v t , k ¬ i + β t ∑ t = 1 V ( n v t , k ¬ i + β t ) p(z_i=k|\vec{z}_{\neg i},W)\propto\frac{n_{k,m\neg i}+\alpha_k}{\sum_{k=1}^K(n_{k,m\neg i}+\alpha_k)}\cdot \frac{n_{v_t,k\neg i}+\beta_t}{\sum_{t=1}^V(n_{v_t,k\neg i}+\beta_t)} p(zi=k∣z¬i,W)∝∑k=1K(nk,m¬i+αk)nk,m¬i+αk⋅∑t=1V(nvt,k¬i+βt)nvt,k¬i+βt
n k , m ¬ i n_{k,m\neg i} nk,m¬i表示第 m m m篇文档除去第 n n n个词后主题 k k k的数目, n v t , k ¬ i n_{v_t,k\neg i} nvt,k¬i表示除去第 m m m篇文档第 n n n个词后的语料中主题 k k k下词 v t v_t vt的数目。(具体推导过程请参考《LDA数学八卦》和博文《通俗理解LDA主题模型》)。
Gibbs采样过程如下:
- 对语料中每一个词 w w w随机初始化一个主题 z z z;
- 对语料中的每一个词,按照概率 p ( z i = k ∣ z ⃗ ¬ i , W ) p(z_i=k|\vec{z}_{\neg i},W) p(zi=k∣z¬i,W)重新采样它的主题,在语料中进行更新;
- 重复第2步的采样过程,直至Gibbs采样收敛;
- 统计语料中的topic-word共现频率矩阵,该矩阵就是LDA模型。
总结
花费两天时间重新理解了一遍LDA主题模型,欢迎多多交流。
参考文献
LDA数学八卦
通俗理解LDA主题模型