CNN卷积神经网络简单介绍与详细搭建注释-识别mnist手写黑白数字
卷积神经网络(CNN)是在计算机视觉中经常用到的的学习模型。(详细注释版代码在后面)
CNN是深度神经网络(DNN)的改进版本,加上了convolution(卷积层)和pooling(池化层)以及padding(填充)操作。
注:下面引用的图片均来自台大李宏毅老师
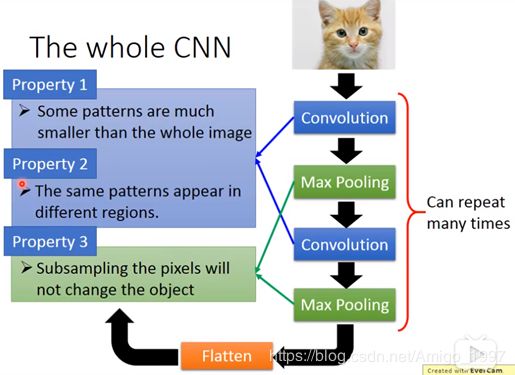
卷积神经网络的结构如上图所示,一个三层张量(RGB图像)的输入,通过多次卷积层和池化层变成具有很多层的张量,再拉平成矩阵输入到全连接层(传统神经网络)。
卷积神经网络的三大优势如上图所示,可以有效浓缩和减少feature。
卷积层演示如上图:这是演示的一个黑白图像(矩阵)和一个卷积核(filter),步长(stride)=1的情况。因为filter是3X3,所以红色框框的大小也是3X3,与filter做内积(位置相同的元素做乘积最后相加),然后红框每次移动一格。6x6的矩阵就成了4x4.
filter的大小和个数,stride的大小都可以自己定义,有2个卷积核所以最后合成的是2层张量。
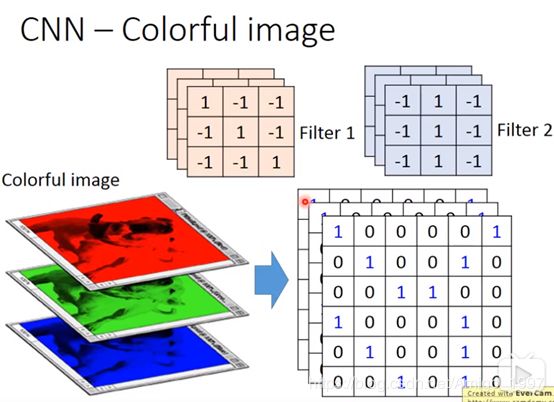
三层的输入(RGB图像)则每个filter本身就是三层,不像之前的filter本身只有一层,这里的filter把3层的东西变成一个点;最后输出的模型有几层就代表有几个卷积核。
通过这样的方式,就不需要全连接和有效减少参数了。
池化层(pooling)就是起到压缩的方式,常见的有取最大的(max)和取平均值(average),例如在2x2的池化层中,有[-1,1,0,3],用最大的方式压缩就只剩下[3],pooling同样有stride,通常是卷积核stride的+1。
填充操作(padding)就是为了防止在步长移动超过原有数据集设计的,valid的方式是舍弃最后一部分数据而same是在周围补0是补步长可以移动。
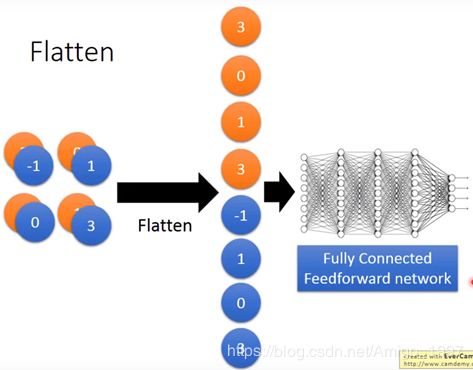
最后把这个已经有很多层的输出拉平成矩阵,输入传统DNN。
以上就是CNN的快速入门,接下来就开始代码实践了!
卷积神经网络搭建演示:
实验环境:jupyter notebook, python3, tensorflow(cpu版), Anaconda, mnist数据集
import tensorflow as tf
import matplotlib.pyplot as plt
%matplotlib inline
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data',one_hot=True) #读取数据0~9
#########################################
###函数名:computer_accuracy ###
###作用: 计算模型的正确率 ###
###输入:验证集的sample和label ###
###输出:模型的正确率 ###
#########################################
def computer_accuracy(v_xs,v_ys):
global prediction
#keep_prob是dropout剩下的比例
y_pre = sess.run(prediction,feed_dict={xs:v_xs,keep_prob:1})
#下行代码因为结果是一个10个数(表示对于数字的概率)的向量
correct_prediction = tf.equal(tf.argmax(y_pre,1),tf.argmax(v_ys,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) #记得先转化数据格式
result = sess.run(accuracy,feed_dict={xs:v_xs,ys:v_ys,keep_prob:1})
return result
#########################################
###函数名:weight_variable ###
###作用:随机初始化权重且维度相同 ###
###输入:输入张量(这里是一维的) ###
###输出:一个具有初始值的权重变量 ###
#########################################
def weight_variable(shape):
initial = tf.truncated_normal(shape,stddev = 0.1)
#从截断的正态分布中输出随机值,stddev是正态分布的标准差
return tf.Variable(initial) #通过构造variable 类的实例来添加一个变量到图中
#########################################
###函数名:bias_variable ###
###作用: 随机初始化偏差且维度相同 ###
###输入: 输入张量 ###
###输出:一个初始值为0.1的偏差变量 ###
#########################################
def bias_variable(shape):
initial = tf.constant(0.1,shape=shape) #y一个常量张量的维度等于输入张量的维度,值为0.1
return tf.Variable(initial)
#########################################
###函数名:conv2d ###
###作用:2维的卷积层 ###
###输入:数据信息 和 权重 ###
###输出:卷积过的数据集 ###
#########################################
def conv2d(x,W):
#步长=[1,x_movement,y_movement,1],padding填充周围有valid和same可选择
return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME')
#########################################
###函数名:max_pool_2x2 ###
###作用:用最大值方法压缩的池化层 ###
###输入:卷积过的数据集 ###
###输出:压缩过的数据集 ###
#########################################
def max_pool_2x2(x):
#ksize是池化窗口的大小=[1,height,width,1],一般height=width=池化窗口的步长
#池化窗口的步长一般是比卷积核多移动一位
return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
#定义placeholder,便于神经网络输入数据
xs = tf.placeholder(tf.float32,[None,784]) #不限sample的个数,每个图片是28x28=784
ys = tf.placeholder(tf.float32,[None,10])
keep_prob = tf.placeholder(tf.float32)
#下行代码中-1表示不限导入图片个数,会自动计算==placeholder里面的None,最后的1表示channel=1,说明#是灰白图像,3则是彩色图像
x_image = tf.reshape(xs,[-1,28,28,1])
#print(x_image.shape) #[number_samples,28,28,1]
##############################网络层搭建-start#######################
##conv1 layer##
#[5,5,1,32]就是输入的张量,5X5是卷积核的大小,1表示输入的通道数为1是黑白的,32是操作后输出图片的
#厚度,表明有32个卷积核
W_conv1 = weight_variable([5,5,1,32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image,W_conv1) + b_conv1) #加上激活函数非线性化处理 #convolution 卷积层
h_pool1 = max_pool_2x2(h_conv1) #池化层 pooling
#h_conv1的outsize 28x28x32 , h_pool1的outsize 14x14x32 因为填充方式padding都是same,但是
#conv的步长是1,而pool的步长是2
##conv2 layer##
W_conv2 = weight_variable([5,5,32,64])#卷积核还是5x5,但是传入的张量维度从1变成了32
#传出的张量维度改为64,表明有64个卷积核
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1,W_conv2) + b_conv2) #加上激活函数非线性化处理 #convolution 卷积层
h_pool2 = max_pool_2x2(h_conv2) #池化层 pooling
#h_conv2的outsize 14x14x64 , h_pool2的outsize 7x7x64
#s上面的卷积层想设置几个设置几个,下面开始写全连接层代码。
##func1 layer##
W_fc1 = weight_variable([7*7*64,1024]) #表明一维张量全连接1024个神经元
b_fc1 = bias_variable([1024]) #要是[卷积核或者神经元个数],[]不可以少因为输入的是张量
#下行代码实现拉平成二维张量(矩阵) [n_samples,7,7,64]->>[n_samples,7*7*64]
h_pool2_flat = tf.reshape(h_pool2,[-1,7*7*64]) #将三维的数据转化为一维的数据
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat,W_fc1) + b_fc1) #矩阵相乘加上bias,result也是一维张量
h_fc1_drop = tf.nn.dropout(h_fc1,keep_prob) #减少overfit
##func2 layer##
W_fc2 = weight_variable([1024,10]) #因为是识别10个数字
b_fc2= bias_variable([10])
prediction = tf.nn.softmax(tf.matmul(h_fc1_drop,W_fc2) + b_fc2) #最后的输出层
############################网络层搭建-end###############################
#通过优化器减少预测值和真实值之间的交叉熵达到训练模型的目的
cross_entropy =tf.reduce_mean(-tf.reduce_sum(ys*tf.log(prediction),reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy) #学习率设置的很小
#可视化为了画折线图
step_list = list(range(10)) # [0,1,2,……,9]
cnn_list = []
fig = plt.figure() #建立可视化图像框
ax = fig.add_subplot(1,1,1) #z子图总行数、列数,位置
ax.set_title('cnn_accuracy ', fontsize=14,y=1.02)
#初始化,如果存在变量则是必不可少的操作
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(500): #训练500次
batch_xs,batch_ys = mnist.train.next_batch(100)
#小批量训练法,每次训练用其中的100个sample,
sess.run(train_step,feed_dict={xs:batch_xs,ys:batch_ys,keep_prob:0.5})
if step%50 ==0:
#下列计算不需要sess.run是因为computer_accuracy函数里面已经有sess.run了
cnn_accuracy = computer_accuracy(mnist.test.images,mnist.test.labels) #mnist.test.images[:1000]
cnn_list.append(cnn_accuracy)
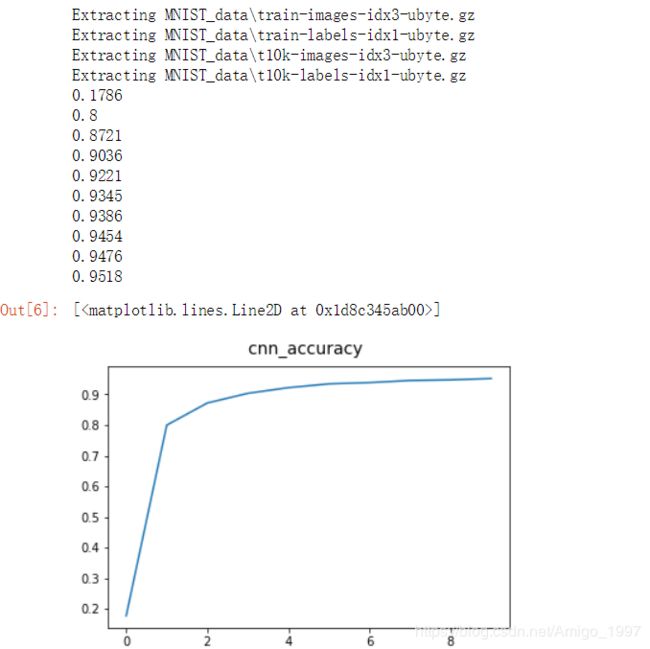
print(cnn_accuracy)
ax.plot(step_list,cnn_list)
###题外话:正确率可以达到95%以上,CPU版本的TF可以让电脑满负荷100%CPU的跑……###实验结果:
参考资料:
莫烦tensorflow视频教程 :https://www.bilibili.com/video/av16001891
李宏毅卷积神经网络原理:https://www.bilibili.com/video/av23593949?from=search&seid=11913427503734628359