python_动态规划—钢条切割例题 实现

学习动态规划问题时，较为经典的分析例题，分别通过递归，备忘录和自下而上的方式基于python实现的练习。

首先由斐波那契数列进行练习：

# 斐波那契数列   递归
def fibo(n):
    if n <= 0:
        return 0
    if n == 1:
        return 1
    return fibo(n-1)+fibo(n-2)

# 斐波那契数列   非递归
（一）自顶向下的备忘录版本

def Fibonacci(n):
    sum_list = [0] * (n + 1)

    def fibo(n, sum_list):
        if sum_list[n] != 0:
            return sum_list[n]
        if n <= 2:
            sum_list[n] = 1
        else:
            sum_list[n] = fibo(n-1, sum_list)+fibo(n-2, sum_list)
        # print(sum_list)
        return sum_list[n]
    return fibo(n, sum_list)

通过定义sum_list列表（n+1个元素）来记录斐波那契数列中每一个值，
如果存在sum_list中的值，省去递归直接进行计算，
如果sum_list中没有斐波那契中的值，
再利用递归进行计算并保存在sum_list中。省去了重复计算。


（二）自低而上
def fibo(n):
    if n <= 1:
        return n
    s1 = 0
    s2 = 1
    sum = 1
    for i in range(1,n):
        sum = s1+ s2
        s1 = s2
        s2 = sum
    return sum


但是备忘录方法还是使用到了递归，并产生额外的开销。
所以，可以先算子问题，fib（1），fib（2），fib（3）……等，
即动态规划核心：先计算子问题再计算父问题。

现在转至切割钢条问题：

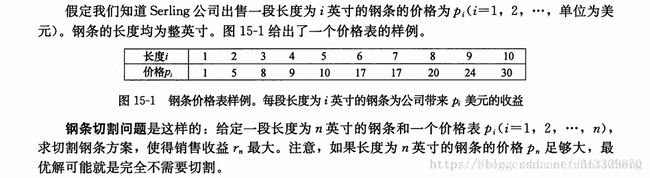
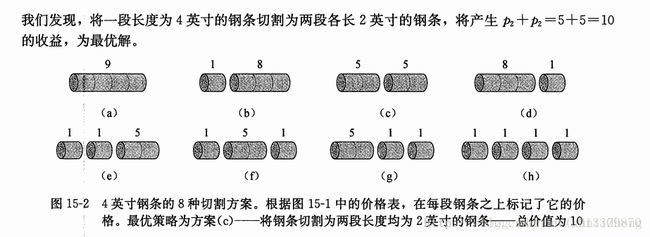
例题：钢条切割

例题来源：算法导论

（一）

# 递归版本
def value_max(p, n):
    if n == 0:
        return 0
    q = 0
    for i in range(0, n):
        q = max(q, p[i]+value_max(p, n-i-1))
    return q

（二）

同斐波那契，多添加了一个max的函数用来筛选，再添加一个列表r用来记录。

# 备忘录版本

def cutMemo(p, n):
    r = [0]* (n+1)

    def value_max(p, n, r):
        if n == 0:
            return 0
        q = 0
        for i in range(0, n):
            q = max(q, p[i] + value_max(p, n-i-1, r))
            r[i] = q
        print(r)
        return q

    return value_max(p, n, r)

（三）

# 自下而上的动态规划
def cutMemo(p, n):
    r = [0] * (n+1)
    for i in range(1, n+1):
        if n == 0:
            return 0
        q = 0
        for j in range(1, i+1):
            q = max(q, p[j-1]+r[i-j])
            r[i] = q
    return r

文章参考自https://blog.csdn.net/u013309870/article/details/75193592