系统学习深度学习(四十)--基于模拟的搜索与蒙特卡罗树搜索(MCTS)
转自:https://www.cnblogs.com/pinard/p/10470571.html
1. 基于模拟的搜索概述
什么是基于模拟的搜索呢?当然主要是两个点:一个是模拟,一个是搜索。模拟我们在上一篇也讨论过,就是基于强化学习模型进行采样,得到样本数据。但是这是数据不是基于和环境交互获得的真实数据,所以是“模拟”。对于搜索,则是为了利用模拟的样本结果来帮我们计算到底应该采用什么样的动作,以实现我们的长期受益最大化。
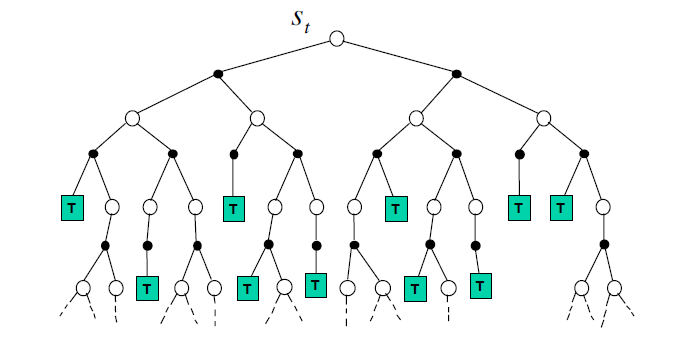
那么为什么要进行基于模拟的搜索呢?在这之前我们先看看最简单的前向搜索(forward search)。前向搜索算法从当前我们考虑的状态节点St开始考虑,怎么考虑呢?对该状态节点所有可能的动作进行扩展,建立一颗以St为根节点的搜索树,这个搜索树也是一个MDP,只是它是以当前状态为根节点,而不是以起始状态为根节点,所以也叫做sub-MDP。我们求解这个sub-MDP问题,然后得到St状态最应该采用的动作At。前向搜索的sub-MDP如下图:
前向搜索建立了一个sub-MDP来求解,这很精确,而且这在状态动作数量都很少的时候没有问题,但是只要稍微状态动作数量多一点,每个状态的选择就都特别慢了,因此不太实用,此时基于模拟的搜索就是一种比较好的折衷。
2. 简单蒙特卡罗搜索
首先我们看看基于模拟的搜索中比较简单的一种方法:简单蒙特卡罗搜索。
简单蒙特卡罗搜索基于一个强化学习模型Mv和一个模拟策略π.在此基础上,对于当前我们要选择动作的状态St, 对每一个可能采样的动作a∈A,都进行K轮采样,这样每个动作a都会得到K组经历完整的状态序列(episode)。即:
![]()
现在对于每个(St,a)组合,我们可以基于蒙特卡罗法来计算其动作价值函数并选择最优的动作了。
![]()
简单蒙特卡罗搜索和起前向搜索比起来,对于状态动作数量的处理能力上了一个数量级,可以处理中等规模的问题。但是假如我们的状态动作数量达到非常大的量级,比如围棋的级别,那么简单蒙特卡罗搜索也太慢了。同时,由于使用蒙特卡罗法计算其动作价值函数,模拟采样得到的一些中间状态和对应行为的价值就被忽略了,这部分数据能不能利用起来呢?
下面我们看看蒙特卡罗树搜索(Monte-Carlo Tree Search,以下简称MCTS)怎么优化这个问题的解决方案。
3. MCTS的原理
MCTS摒弃了简单蒙特卡罗搜索里面对当前状态St每个动作都要进行K次模拟采样的做法,而是总共对当前状态St进行K次采样,这样采样到的动作只是动作全集A中的一部分。这样做大大降低了采样的数量和采样后的搜索计算。当然,代价是可能动作全集中的很多动作都没有采样到,可能错失好的动作选择,这是一个算法设计上的折衷。
在MCTS中,基于一个强化学习模型Mv和一个模拟策略π,当前状态St对应的完整的状态序列(episode)是这样的:
![]()
采样完毕后,我们可以基于采样的结果构建一颗MCTS的搜索树,然后近似计算Q(st,a)和最大Q(st,a)对应的动作。
![]()
MCTS搜索的策略分为两个阶段:第一个是树内策略(tree policy):为当模拟采样得到的状态存在于当前的MCTS时使用的策略。树内策略可以使ϵ−贪婪策略,随着模拟的进行策略可以得到持续改善,还可以使用上限置信区间算法UCT,这在棋类游戏中很普遍;第二个是默认策略(default policy):如果当前状态不在MCTS内,使用默认策略来完成整个状态序列的采样,并把当前状态纳入到搜索树中。默认策略可以使随机策略或基于目标价值函数的策略。
这里讲到的是最经典的强化学习终MCTS的用户,每一步都有延时奖励,但是在棋类之类的零和问题中,中间状态是没有明确奖励的,我们只有在棋下完后知道输赢了才能对前面的动作进行状态奖励,对于这类问题我们的MCTS需要做一些结构上的细化。
4. 上限置信区间算法UCT
在讨论棋类游戏的MCTS搜索之前,我们先熟悉下上限置信区间算法(Upper Confidence Bound Applied to Trees, 以下简称UCT)。它是一种策略算法,我们之前最常用的是ϵ−贪婪策略。但是在棋类问题中,UCT更常使用。
在棋类游戏中,经常有这样的问题,我们发现在某种棋的状态下,有2个可选动作,第一个动作历史棋局中是0胜1负,第二个动作历史棋局中是8胜10负,那么我们应该选择哪个动作好呢?如果按ϵ−贪婪策略,则第二个动作非常容易被选择到。但是其实虽然第一个动作胜利0%,但是很可能是因为这个动作的历史棋局少,数据不够导致的,很可能该动作也是一个不错的动作。那么我们如何在最优策略和探索度达到一个选择平衡呢?ϵ−贪婪策略可以用,但是UCT是一个更不错的选择。
UCT首先计算每一个可选动作节点对应的分数,这个分数考虑了历史最优策略和探索度,一个常用的公式如下:
其中,wi是 i 节点的胜利次数,ni 是i节点的模拟次数,Ni是所有模拟次数,c 是探索常数,理论值为√2,可根据经验调整,c 越大就越偏向于广度搜索,c 越小就越偏向于深度搜索。最后我们选择分数最高的动作节点。
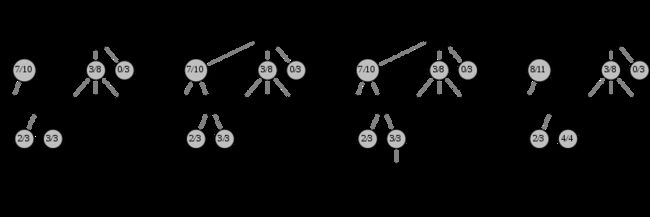
比如对于下面的棋局,对于根节点来说,有3个选择,第一个选择7胜3负,第二个选择5胜3负,第三个选择0胜3负。
如果我们取c=10,则第一个节点的分数为:
第二个节点的分数为:
第三个节点的分数为:
可见,由于我们把探索率c设置的比较大,第三个节点是被UCT选中要执行的动作节点。当然如果我们把c设置的比较小的话,第一个或者第二个可能就变成最大的分数了。
5. 棋类游戏MCTS搜索
在像中国象棋,围棋这样的零和问题中,一个动作只有在棋局结束才能拿到真正的奖励,因此我们对MCTS的搜索步骤和树结构上需要根据问题的不同做一些细化。
对于MCTS的树结构,如果是最简单的方法,只需要在节点上保存状态对应的历史胜负记录。在每条边上保存采样的动作。这样MCTS的搜索需要走4步,如下图(图来自维基百科):
第一步是选择(Selection):这一步会从根节点开始,每次都选一个“最值得搜索的子节点”,一般使用UCT选择分数最高的节点,直到来到一个“存在未扩展的子节点”的节点,如图中的 3/3 节点。之所以叫做“存在未扩展的子节点”,是因为这个局面存在未走过的后续着法,也就是MCTS中没有后续的动作可以参考了。这时我们进入第二步。
第二步是扩展(Expansion),在这个搜索到的存在未扩展的子节点,加上一个0/0的子节点,表示没有历史记录参考。这时我们进入第三步。
第三步是仿真(simulation),从上面这个没有试过的着法开始,用一个简单策略比如快速走子策略(Rollout policy)走到底,得到一个胜负结果。快速走子策略一般适合选择走子很快可能不是很精确的策略。因为如果这个策略走得慢,结果虽然会更准确,但由于耗时多了,在单位时间内的模拟次数就少了,所以不一定会棋力更强,有可能会更弱。这也是为什么我们一般只模拟一次,因为如果模拟多次,虽然更准确,但更慢。
第四步是回溯(backpropagation), 将我们最后得到的胜负结果回溯加到MCTS树结构上。注意除了之前的MCTS树要回溯外,新加入的节点也要加上一次胜负历史记录,如上图最右边所示。
以上就是MCTS搜索的整个过程。这4步一般是通用的,但是MCTS树结构上保存的内容而一般根据要解决的问题和建模的复杂度而不同。
6. MCTS小结
MCTS通过采样建立MCTS搜索树,并基于4大步骤选择,扩展,仿真和回溯来持续优化树内的策略,进而可以帮助对状态下的动作进行选择,非常适合状态数,动作数海量的强化学习问题。比如AlphaGo和AlphaGo Zero都重度使用了MCTS搜索,我们在下一篇讨论AlphaGo Zero如何结合MCTS和神经网络来求解围棋强化学习问题。