【机器学习】十三、一文看懂Bagging和随机森林算法原理
集成学习主要包括Boosting(提升)和Bagging(袋装)两大类，本文主要分享第二类Bagging类集成学习，会讲解Bagging的原理，以及在Bagging基础上改进之后的随机森林(Random Forest，简称RF)算法。码字不易，喜欢请点赞！！！
一、集成学习
1.1 集成学习简介
集成学习(Ensemble Learning)，通过组合多个基学习器来完成任务。可用于分类、回归、异常点检测、特征选取集成等。是现在非常火爆的机器学习方法。
1.2 集成学习种类
集成学习就是将一些基学习器组合成一个强学习器。对于这些基学习器来说，可以选择同一种类的，比如随机森林都采用决策树作为基学习器；也可以选择不全相同的类别的。但是一般来说都采用同质的基学习器，目前来说，应用的最广泛的基学习器是决策树和神经网络。
同质学习器按照基学习器之间是否存在依赖关系可以分为两类：
- 基学习器之间存在依赖关系：代表算法为Boosting算法
- 基学习器之间无依赖关系(可并行生成)：代表算法为Bagging算法
1.2.1 Boosting原理
Boosting原理如下图，首先在训练集中用初始权重训练Model1，根据Model1中的学习误差率来更新训练样本的权重，使得Model1中的学习误差率高的样本点的权重变高，那么在Model2中这些样本将会更受重视；如此重复迭代，直接达到达到T个基学习器。最终将这T个基学习器通过集合策略进行整合，得到最终的强学习器。
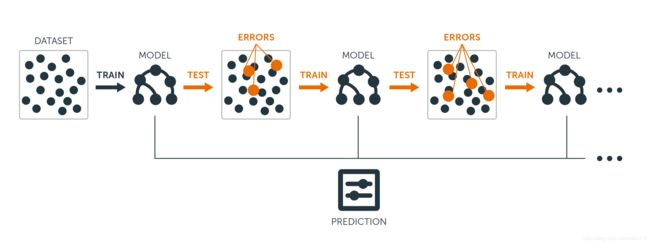Boosting系列算法里最著名算法主要有AdaBoost算法和提升树(boosting tree)系列算法。之后我们会进行讲解介绍。
1.2.2 Bagging原理
上面说到Boosting算法的基学习器之间是具有关联的状态的，而Bagging在这一点上则不同，Bagging算法的基学习器之间是没有关联的。如下图：
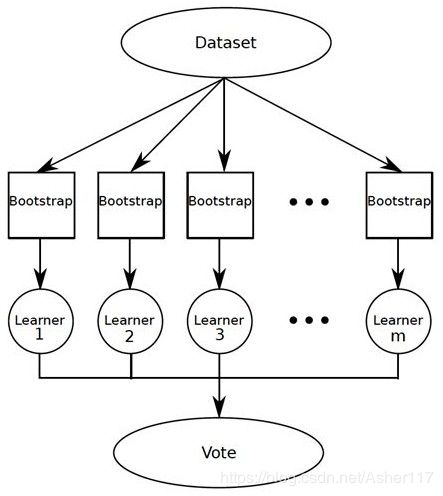
先从数据集DataSet中通过自助采样的方法，采集样本，然后每个样本跑一个基学习器，最后通过组合这些基学习器来完成任务。
二、Bagging
2.1 采样方法
上面说到Bagging算法的基学习器之间是没有关联的。
对于具有M个样本，和T个基学习器的Bagging算法。
首先针对每个基学习器 t i t_i ti，我们对样本M采用自助采样法(Bootstrap Sampling)进行采样(就是我们知道的有放回抽样)，抽取M个样本。
对于某个样本，在每次抽样，被抽到的概率为 1 / M 1/M 1/M，不被抽到的概率为 1 − 1 / M 1-1/M 1−1/M，则M次抽样不被抽到的概率为 ( 1 − 1 M ) M (1-\frac{1}{M})^M (1−M1)M，当M趋近于∞时， ( 1 − 1 M ) M = 1 e = 0.368 (1-\frac{1}{M})^M=\frac{1}{e}=0.368 (1−M1)M=e1=0.368，也就是说对于每个基学习器的样本，约有36.8%的样本不会被采集，这部分没有被采集的样本称为袋外样本(Out Of Bags，简称OOB)。这些数据没有参加基学习器模型的训练，因此可以提高模型的泛化能力。
2.2 Bagging流程
输入：M个样本 ( x 1 , y 1 ) ， ( x 2 , y 2 ) ， . . . ， ( x m , y m ) (x_1,y_1)，(x_2,y_2)，...，(x_m,y_m) (x1,y1)，(x2,y2)，...，(xm,ym)，基学习器个数T
输出：强学习器 f ( x ) f(x) f(x)
for i from 1 to T:
在样本集M中有放回采样M个样本Mi,
对样本Mi训练处基学习器Ti
组合T个基学习器得到最终的强学习器f(x)
任务：
- 预测：将T个基学习器的预测结果采用平均值(或加权平均值)作为最终的预测结果
- 分类：将T个基学习器的预测类别最多的一类作为结果
三、随机森林
3.1 采样方法
随机森林，简称RF，采用CART作为基学习器，是在Bagging上的一种改进。采样方法同Bagging算法，采用自助采样法。
3.2 随机森林流程
随机森林的改进在于对于普通的决策树，如果样本具有n个特征，不同于普通的决策树在节点上所有的n个样本特征中选择一个最优的特征来做决策树的左右子树划分。RF首先会随机选择 n s u b n_{sub} nsub个特征，然后在这些随机选择的 n s u b n_{sub} nsub个样本特征中，选择一个最优的特征来做决策树的左右子树划分。这样进一步增强了模型的泛化能力。
这一点是RF(取部分特征)和Bagging(取所有特征)最大的不同。
输入：M个样本 ( x 1 , y 1 ) ， ( x 2 , y 2 ) ， . . . ， ( x m , y m ) (x_1,y_1)，(x_2,y_2)，...，(x_m,y_m) (x1,y1)，(x2,y2)，...，(xm,ym)，基学习器个数T，模型特征数 n s u b n_{sub} nsub
输出：强学习器 f ( x ) f(x) f(x)
for i from 1 to T:
在样本集M中有放回采样M个样本Mi,随机选择n_sub个特征fi
对样本Mi在fi个特征上训练处基学习器Ti
组合T个基学习器得到最终的强学习器f(x)
任务：
- 预测：将T个基学习器的预测结果采用平均值(或加权平均值)作为最终的预测结果
- 分类：将T个基学习器的预测类别最多的一类作为结果
3.3 随机森林优缺点
- 优点
- 训练可以高度并行化，对于大数据时代的大样本训练速度有优势。
- 由于可以随机选择决策树节点划分特征，这样在样本特征维度很高的时候，仍然能高效的训练模型。
- 在训练后，可以给出各个特征对于输出的重要性.
- 由于采用了随机采样，训练出的模型的方差小，泛化能力强。
- 相对于Boosting系列的Adaboost和GBDT， RF实现比较简单。
- 对部分特征缺失不敏感。
- 缺点
- 在某些噪音比较大的样本集上，RF模型容易陷入过拟合。
- 取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果。
参考文献：
李航 《统计学习方法》
https://www.cnblogs.com/pinard/p/6156009.html