no2 神经网络

反向传播

求导链式法则+反向计算

训练过程：通过前向传播得到损失，反向传播得到梯度（ ∂L∂w ），最后用梯度更新权重。

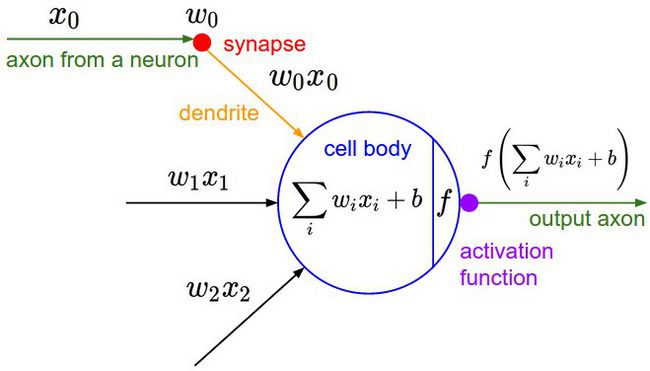
一个神经元的运算

那么 ∂L∂x=∂L∂z∂z∂x ， ∂L∂y=∂L∂z∂z∂y ， ∂L∂w=∂L∂z∂z∂w 。通过这种方式，我们就可以从输出的节点开始，往输入节点的方向计算损失关于各个节点权重的导数值，从而用梯度下降法进行权重的迭代，利用最优化减少损失。

• 和数学归纳法类似，已知了最右边的损失L，通过求导进行反向传播就可以计算出另一个节点的右边的导数，每一个节点都有下一个节点，所以都可以求出其导数。

举一个比较实际的例子

计算如下的一个式子：

f(x,y)=x+σ(y)σ(x)+(x+y)2

通过添加中间变量，进行的正向传播。

x = 3 # example values
y = -4

# forward pass
sigy = 1.0 / (1 + math.exp(-y)) # sigmoid in numerator   #(1)
num = x + sigy # numerator                               #(2)
sigx = 1.0 / (1 + math.exp(-x)) # sigmoid in denominator #(3)
xpy = x + y                                              #(4)
xpysqr = xpy**2                                          #(5)
den = sigx + xpysqr # denominator                        #(6)
invden = 1.0 / den                                       #(7)
f = num * invden # done!                                 #(8)

反向传播计算各个变量权重的导数

# backprop f = num * invden
dnum = invden # gradient on numerator                             #(8)
dinvden = num                                                     #(8)
# backprop invden = 1.0 / den 
dden = (-1.0 / (den**2)) * dinvden                                #(7)
# backprop den = sigx + xpysqr
dsigx = (1) * dden                                                #(6)
dxpysqr = (1) * dden                                              #(6)
# backprop xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# backprop xpy = x + y
dx = (1) * dxpy                                                   #(4)
dy = (1) * dxpy                                                   #(4)
# backprop sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # Notice += !! See notes below  #(3)
# backprop num = x + sigy
dx += (1) * dnum                                                  #(2)
dsigy = (1) * dnum                                                #(2)
# backprop sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy                                 #(1)
# done! phew

向量化反向传播（层与层之间）：

# forward pass
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)

# now suppose we had the gradient on D from above in the circuit
dD = np.random.randn(*D.shape) # same shape as D
dW = dD.dot(X.T) #.T gives the transpose of the matrix
dX = W.T.dot(dD)

• 注意分析各个矩阵的形状，比如说X是(10,3)，dD是(5,3)，那么要得到(5,10)的dW，我们就需要dW = dD.dot(X.T)

细节

CIFAR-10的基本神经网络识别思路

1. 输入层是一个3072大小的向量，是将一张图片3通道的颜色值拉伸成一个向量
2. 权重W1，隐藏层的输入是XW1，然后使用RuLU激活函数，得到隐藏层的输出， o=max(0,XW1)
3. oW2是输出层的输出， s=oW2 ，s是该图片属于各个类的分数
4. 其中权重W1和W2就是需要用梯度下降法学习的网络参数

Tips.

1. 不需要太多的数据，可以使用迁移学习，选择一些别人训练好的网络，取他们的前部分，当作类似于特征提取的功能模块，然后训练最后几层，就可以节省数据
2. 不要觉得计算量大就无脑增加数据

激活函数的选择

激活函数在神经元的中间，将输入转化为输出。 out=f(XW+b) ，其中的f就是激活函数。

sigmoid

σ(x)=1/(1+e−x)

优缺点：

1. 输出控制在[0,1]之间
2. 深度学习领域开始时使用频率最高，而且可以解释为神经元的激活率
3. 输入很大或者很小的时候，会导致导数 ∂σ∂x 很小，再加上其导数的最大值是0.25，这意味着在反向传播的时候，导数在每一层至少会被压缩为原来的1/4，导数越来越小以至于对权重的更新很小，从而引起梯度弥散(gradient vanishing)
4. 输出不是0均值的，这里输入全为正，导致在反向传播的时候权重W全为正或者全为负。使用batch可以缓解这个问题
5. exp幂运算比较耗时

梯度弥散：由于很多原因，比如说层数太多等，导致反向传播的时候梯度变小，前面权重进行更新的时候变化非常小，以至于不能够从样本中进行有效的学习。

tanh

tanh(x)=2σ(2x)−1

优缺点：

1. 输出控制在[-1,1]之间
2. 输出是0均值的
3. 输入很大或者很小的时候，会导致导数很小，从而引起梯度弥散(gradient vanishing)

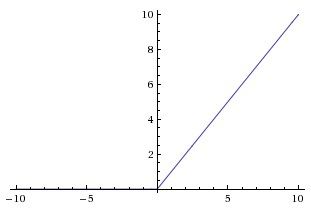
ReLU(Rectified Linear Unit)

f(x)=max(0,x)

优缺点：

1. 在大于0的区域不会饱和，也就是说导数不会变得很小
2. 计算效率高
3. 收敛速度比sigmoid和tanh快，比如有的快了6倍
4. 输出不是0均值的
5. 在输入小于0的区域会梯度消失，神经元处于非激活状态，无法进行反向传播，权重也无法进行更新，大于0的区域梯度直接向前传播
6. 存在一些死掉的神经元，即任何数据都不能激活它(wx+b<0)，通常是由于学习率太高，梯度流很大，权重一下子就更新了很多，也可能是初始化权重策略，可以在训练时统计来检查，初始化的时候把偏置设置成一个比较小的正数

Leaky ReLU

f(x)=max(αx,x)

其中 α 是一个很小的常量，比如说0.01，也可以通过反向传播去训练

优缺点：同ReLU，但是改进了5和6，神经元就算在输入小于0的区域也不会梯度消失，不会有非激活状态

ELU(Exponential Linear Units)

f(x)={x,α(expx−1),if x>0otherwise

优缺点：

1. 不会有Dead ReLU（神经元失活）问题
2. 输出的均值接近0，zero-centered
3. 幂运算计算效率高
4. 其他同ReLU

Maxout

f(x)=max(wT1x+b1,wT2x+b2)

优缺点：统一了ReLU和Leaky ReLU，在神经元的计算上多了非线性的元素，但是计算参数数量多了一倍。

总结

1. 优先考虑ReLu，但是要注意学习率，并注意网络中神经元的失活问题
2. 可以尝试使用Leaky ReLU, Maxout, ELU
3. 也可以尝试使用tanh，但是期望不要太大
4. 不要使用sigmoid

神经网络结构

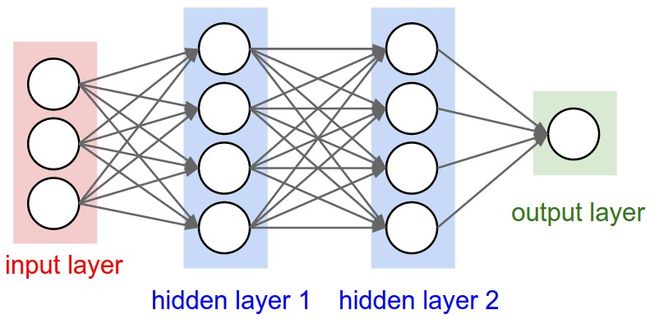
通常的网络按层来组织，每层中都有神经元，没有回路。这种层的组织结构可以很轻松的进行向量矩阵的运算，容易理解和实现，并且效率高。全连接层（fully-connected layer）是很常见的一种结构，表示相邻两层之间的神经元两两连接。下面是两个例子。

命名规则，N-层神经网络，N包括隐藏层和输出层，不包括输入层。

输出层不像神经网络的其他层，一般没有激活函数，因为最后输出层的输出在分类问题中是代表类的分数，在回归问题中是实值数。

神经网络的规模，通常用参数的数量，或者神经元的数量来衡量网络的规模。例如在图的例子中，第一个网络有 [3×4]+[4×2]=20 个权重，4+2个偏置，总共26个参数，或者有4+2个神经元（不包括输入层）。

确定隐藏层层数和规模

网络规模越大，容量越大，能表示的不同的函数越多。如下是一个二分类的例子，一个隐藏层。

从上图中可以看到，随着隐藏神经元的增大，可以代表越复杂的函数，但是也有过拟合的风险（拟合太好，以至于把训练数据的噪声给拟合进去了），如上图中的右图，将异常点拟合进去，可能会导致模型的泛化能力差，也就是在测试集上表现差。

在实际使用中，尽量使用大的网络，因为过拟合可以通过正则化等方法修补，但是网络太小导致不能表达需要的函数是不能修补的。

数据预处理

对于一个原始数据X[N,D]，其中N是样本数量，D是特征数量。可以做如下的操作：

1. 0均值化

   X -= np.mean(X, axis=0)

   有两种处理方式，以CIFAR-10为例，其中的图片是[32,32,3]。

   1. 生成均值图片，大小为[32,32,3]，是所有图片的平均，然后让每张图片都减去这张均值图片。(AlexNet)
   2. 通道均值，得到3个通道的均值，然后让每张图片都减去对应的均值。(VGGNet)

2. 归一化(normalized data)。归一化的方法很多，不一定必须是如下的方法，比如最大最小值归一化。图像处理中很少使用归一化，因为像素的尺度是一致的，都是[0,255]

   X /= np.std(X, axis=0)

   

3. 根据协方差，可以使用PCA主成份分析，或者白化，降低特征之间的相关性，使特征具有相同的方差。在机器学习中比较常见，在图像处理中比较少
   

   • 注意0均值化中，训练集、验证集、测试集减去的都是训练集的均值

权重初始化

初始化为0显然不是一个很好的选择，因为这样那么对于每个神经元，输出和梯度都是一样的，那么他们做的操作都是一样的。

1. 生成小的随机数来初始化权重，比如说N(0,0.01)

   W = 0.01*np.random.randn(D, H)

   这种方法对于小网络适用，但是对于层数比较深的网络不行。每次乘上W，权重太小（0.01），会导致输入越来越小，梯度也会越来越小，从而导致梯度弥散；权重过大（1），会导致输入越来越大，如果使用tanh或sigmoid，过大的输入会让导数接近0，从而梯度弥散，无法训练权重。

2. Xavier，确保在xw前后数据的方差一致，那么权重如下，其中n是输入的维度数 s=∑niwixi 。在tanh中有效，但是在ReLU中输入到0更快，需要加上因子2

   w = np.random.randn(n) / sqrt(n)
   w = np.random.randn(n) * sqrt(2.0/n) # ReLU

   • 偏置一般初始化为0，使用ReLU，权重初始化使用ReLU的初始化。

Batch Normalization

一般设置在全连接层或者卷积层的后面和非线性层（激活函数）的前面。

Batch Normalization论文地址
论文的中文整理博客

在测试的时候依然使用如下式子：

x^=x−E[x]Var[x]+ϵ−−−−−−−−√

这里的均值和方差已经不是针对某一个Batch了，而是针对整个数据集而言。因此，在训练过程中除了正常的前向传播和反向求导之外，我们还要记录每一个Batch的均值和方差，以便训练完成之后按照下式计算整体的均值和方差：

E[x]←EB[μB]

Var[x]←mm−1EB[σ2B]

反向传播的导数：

∂l∂x^i∂l∂σ2B∂l∂μB∂l∂xi∂l∂γ∂l∂β======∂l∂yi⋅γ∑i=1m∂l∂x^i⋅(xi−μB)⋅−12(σ2B+ϵ)−3/2(∑i=1m∂l∂x^i⋅−1σ2B+ϵ−−−−−√)+∂l∂σ2B⋅∑mi=1−2(xi−μB)m∂l∂x^i⋅1σ2B+ϵ−−−−−√+∂l∂σ2B⋅2(xi−μB)m+∂l∂μB⋅1m∑i=1m∂l∂yi⋅x^i∑i=1m∂l∂yi

作者在文章中说应该把BN放在激活函数之前，这是因为Wx+b具有更加一致和非稀疏的分布。但是也有人做实验表明放在激活函数后面效果更好。这是实验链接，里面有很多有意思的对比实验。

1. 提高了整个网络的梯度流
2. 可以设置更高的学习率
3. 减少了对初始值的依赖
4. 有一定正则化的作用，减少了对Dropout的需要

损失函数

损失是为了量化预测值和实际值之间的差距，差距越大损失越大。数据损失L是所有样本损失的平均， L=1N∑iLi ，缩写f是网络的输出，我们的预测值。对于不同的问题有集中不同的输出。

分类问题

只有一个正确答案的分类问题，常用的有svm和softmax损失函数。

Li=∑j≠yimax(0,fj−fyi+1)

Li=−log⎛⎝efyi∑jefj⎞⎠

大量类别的，比如说英文字典，或者ImageNet包含了22000个类别。可以使用分层的Softmaxpdf here。先创建一棵类别树，每一个节点用于softmax，树的结构对分类效果影响很大，需要具体问题具体分析。

属性分类，一个样本有好几个分类属性，也有可能一个也没有。有两种计算方法，其一是给每个属性单独的设置一个二元分类器（类似于svm）。

Li=∑jmax(0,1−yijfj)

其二是给每个属性单独的设置一个逻辑斯特回归分类器（类似于softmax）。

P(y=1∣x;w,b)=11+e−(wTx+b)=σ(wTx+b)

loss是对概率的对数最大似然估计如下。

Li=∑jyijlog(σ(fj))+(1−yij)log(1−σ(fj))

其中 σ 是sigmoid函数。对其求导结果： ∂Li/∂fj=yij−σ(fj)

回归问题

回归问题是预测实值，例如通过房子的面积来预测房子的价格。常见的通过L1或者L2范式来衡量预测值和实际值之间的差距。

Li=∥f−yi∥22

Li=∥f−yi∥1=∑j∣fj−(yi)j∣

Note：L2损失比Softmax损失更难优化，因为需要对样本的每个值都准确的预测一个正确值，包括异常值。在遇到一个回归问题的时候，首先考虑是否可以转化为分类问题，比如说给某个产品星级评分1-5星，用5个分类器可能比回归更好。

正则化方法

用于控制网络的容量，不让模型过于复杂，从而防止过拟合，增加模型的泛化能力。

L2正则化

最常用的正则化形式。在计算损失loss的时候，加上 12λW2 作为最后的损失，在反向传播计算权重w导数的时候，根据求导法则加上对正则项的导数 λ∗W 。乘上0.5是为了求导的时候格式好看。L2正则项是为了能够充分利用各个特征项。

L1正则化

给损失加上 λ|w| 。也可以同时加上L1和L2正则项。L1正则化项得到的权重会更加稀疏，起到一个类似于特征选择的效果，选择重要的特征进行预测，而滤去噪声。如果没有做过特征选择，那么用L1会有更好的效果。

Max norm constraints

最大范数约束主要思路是安照正常进行update，只不过每次更新之后检查其范数是否大约了设定值 ||w⃗ ||2<x 的经典取值是3或者4。

Dropout

一种很有效、简单的正则化技术，Dropout: A Simple Way to Prevent Neural Networks from Overfitting，基本思想是训练的时候选择一部分的神经元工作。


神经元以P或者0的概率决定是否被使用，测试的时候全部的神经元都是可用的。

一个3层神经网络的例子

""" Vanilla Dropout: Not recommended implementation (see notes below) """

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  """ X contains the data """

  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = np.random.rand(*H1.shape) < p # first dropout mask
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p # second dropout mask
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3

  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)

def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
  out = np.dot(W3, H2) + b3

上面我们没有对输入层进行dropout（也可以做），输出层加入了p这一乘积项，这是因为训练的时候某个神经单元被使用的概率是p，如果他的输出是x那么他训练时输出值的期望只是px，所以在预测阶段要乘以p，但是并不推荐这样做。因为在预测阶段进行操作无异于增加了预测时间。我们用inverted dropout来解决这个问题。在预测时不再乘以p，而是在预测时除以p。

""" 
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3

  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)

def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  out = np.dot(W3, H2) + b3

Bias regularization

bias不与输入变量直接相乘，不能控制数据对最终目标的影响，所以表示一般不用regularization，但是它的数量相对于w很少，约束下也不会有太大的影响。

Per-layer regularization

用的很少，对不同的层使用不同的正则化方法。

实际使用

1. 最常见的是交叉验证单独使用全局的L2正则化
2. 将L2正则化配合dropout也比较常见，其中p的值一般默认是0.5，可以在验证集调参

网络学习

前面介绍了网络的连接结构、数据预处理以及损失函数，这一节介绍学习参数的过程和超参数调参。

梯度检验

通过比较网络中公式计算的梯度和数值法得到的梯度是否相似，来判断网络的梯度部分是否正确。

数值法计算梯度

df(x)dx=f(x+h)−f(x)h

通过泰勒展开可以知道下面的公式误差更小。

df(x)dx=f(x+h)−f(x−h)2h

相对误差

对于不同的问题，梯度的尺度不一样，所以用相对误差来衡量两者的误差。

∣f′a−f′n∣max(∣f′a∣,∣f′n∣)

原来的公式分母是两者之一，但是为了保证ReLU分母不为0，所以就取两者的最大值。

1. relative error > 1e-2 一般来说梯度计算出了问题
2. 1e-2 > relative error > 1e-4 可能有问题了
3. 1e-4 > relative error不光滑的激励函数来说时可以接受的，但是如果使用平滑的激励函数如 tanh nonlinearities and softmax，这个结果还是太高了。
4. 1e-7 通过

需要注意的是网络越深误差越大，如果网络有10层，那么1e-2也可以接受。

• 使用double双精度，降低精度会使误差变大
• 注意浮点数的活动范围， “What Every Computer Scientist Should Know About Floating-Point Arithmetic”。这篇文献介绍的浮点型，可以纠正一些错误。数字过小会导致很多错误，比如说梯度1e-10，那么计算数值误差和解析误差的时候就会出问题。
• kinks 目标函数的不光滑，Kinks是指目标函数不能完全可微的情况可以由之前我们提到的ReLU 、SVM loss，Maxout 等。如果我们要检验的是在x=−1e6时的ReLU的梯度。x<0时analytic gradient一定为0。然而如果我们区的h稍微大一点就会使f(x+h)跨过0点，数值法得到的梯度就不会为0了，这种情况经常发生。神经网络和SVM分类会因为ReLU出现更多的kink。我们可以通过跟踪max(x,y)中较大的一个判断是否有kink出现如果在向前计算的时候x或者y最大，但是在计算 f(x+h) 和 f(x−h)时至少有一个的最大值变化了，说明存在kink了。
• 使用少量的样本数据可以避免kink，同时提高梯度检验的效率
• 步长h越小越小，但是不能太小，否则会有数值精度问题，一般设置为1e-4或者1e-6。维基百科中介绍了h和数值梯度误差之间的关系
• 我们的梯度检查中，检查的是一部分的点，并不是这些点正确就代表全局正确，我们必须选择尽量典型的点作为检查的对象。另外随机初始化可能不是参数空间中最“特征”的点，实际上可能会引入一些病态的情况，在这种情况下，梯度似乎得到了正确的实现，但并非如此。例如，一个带有非常小的权重初始化的SVM将所有数据的分数几乎都为零。梯度的不正确实现仍然可以产生这种模式，并不能推广到比其他分数更大的更有特征的操作模式。
• 正则项的梯度太大盖过了数据的梯度从而导致梯度检验出错。可以在梯度检验的时候关掉正则项，或者单独检查正则项的梯度，确认对数据的梯度影响。
• 关掉dropout和数据增强，也可以设置随机数种子
• 实际中会有百万级的参数梯度，一般检查部分少量的维度，需要注意的是维度中每个独立的参数都要检验

学习之前的完整性检验

1. 用小的参数初始化参数，关掉正则化，单独检查损失函数的损失。比如CIFAR-10中使用Softmax分类器，预计初始损失为2.303，因为10个类，平均一个类的概率为0.1， −ln(0.1)=2.302 ，比如Weston Watkins SVM，预计初始损失为9，因为所有分数接近0，边界为1。如果得到的损失和预计的不一致，那么初始化可能有错误
2. 增加正则化系数，损失因为会增加
3. 过拟合少量数据（比如20个样本）。关掉正则化，取少量样本，训练至损失为0，说明网络可以学习。当然就算过拟合了也可能有问题，比如说样本特征由于某些错误随机了，仍然会过拟合，但是在泛化能力基本没有。

Babysitting Learning process

有很多图可以实时查看网络的训练状态。下面的图的x轴单位是epochs，表示数据集迭代的次数。因为iterations（反向传播次数）取决于batch size，所以epochs更有意义。

Loss function

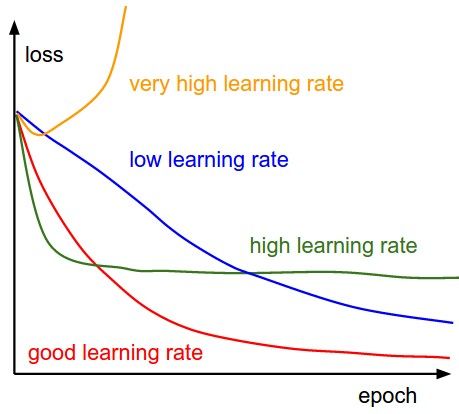
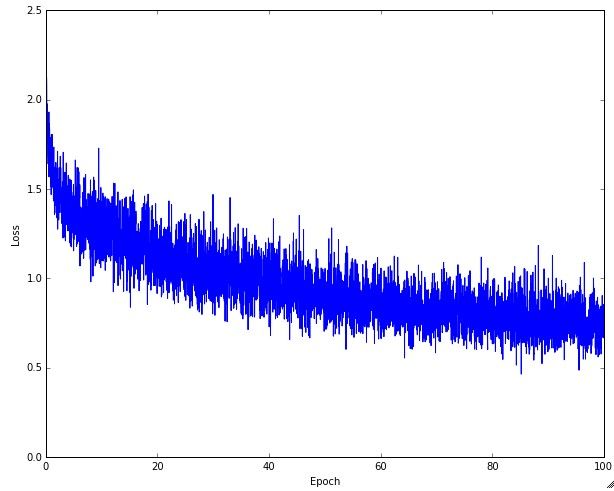
学习率太小看着像是线性的，高的学习率刚开始是指数型的，太高的学习率最后的结果会不好。

• 上下抖动和batch size有关，越大抖动越小。
• 有人喜欢将其在log空间中绘图，曲线可能会就更直一些
• 可以将多个交叉验证的模型一起绘制，可以直观的看出不同点。

Train/Val accuracy

通过验证集训练集的准确率，可以看模型是否过拟合。

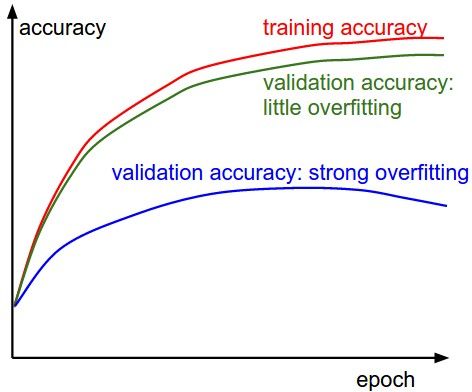
模型过拟合可以增加正则化、增加数据。如果验证集准确率和训练集准确率差不多，那么表示模型规模不够，通过增加参数数量来增大模型规模。

Ratio of weights:updates 权重更新率

观察权重更新的快慢可以知道学习速度learning rate 设定的大小是否合适，下面是权重更新率计算的过程，一般来说在值小于1e-3的时候说明学习效率设定的太小，大于的时候说明设置的太大。

# assume parameter vector W and its gradient vector dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW # simple SGD update
update_scale = np.linalg.norm(update.ravel())
W += update # the actual update
print update_scale / param_scale # want ~1e-3

Activation/Gradient distributions per layers 每层的激活函数、梯度分布

初始化出错会降低甚至停止学习过程，可以通过网络中每一层的激活输出和梯度的直方图来查看。比如说看到所有激活函数输出都为0，或者对于tanh激活函数，输出不是-1就是1等。

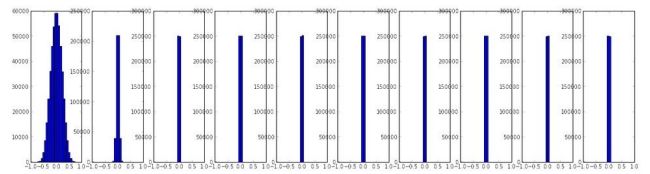
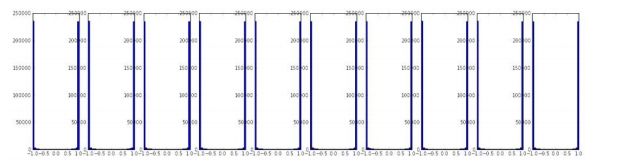
First-layer Visualizations

如果是在处理图片可以将第一层可视化：

下图第二个是一个非常合理的结果：特征多样，比较干净、平滑。但是第一个图很粗糙，显示不出底层特征，可能是因为网络不收敛或者学习速率设置不好或者是因为惩罚因子设置的太小。

参数更新

本节介绍使用梯度来对参数进行更新的方法。

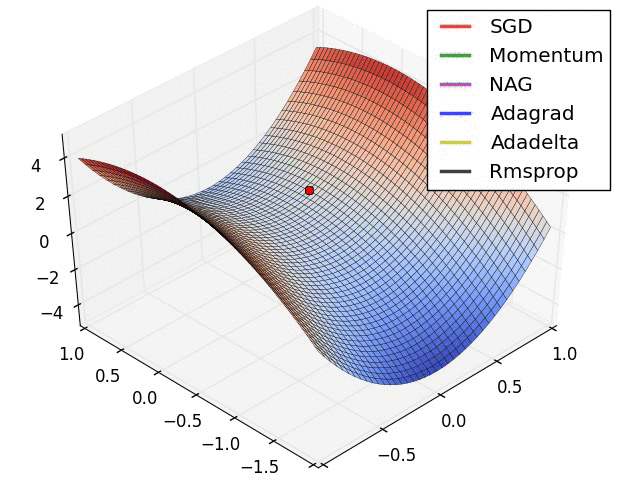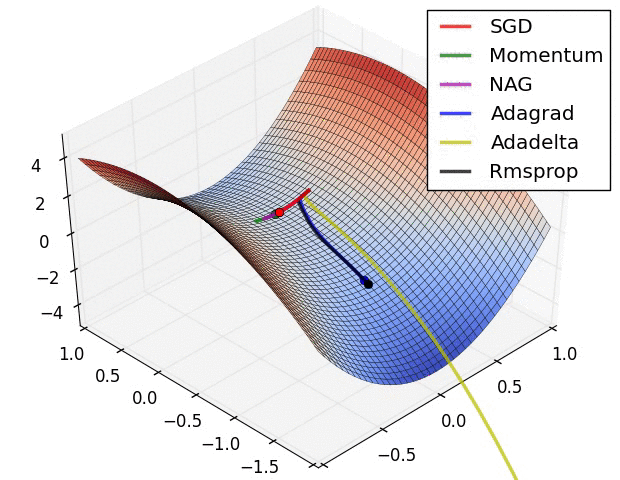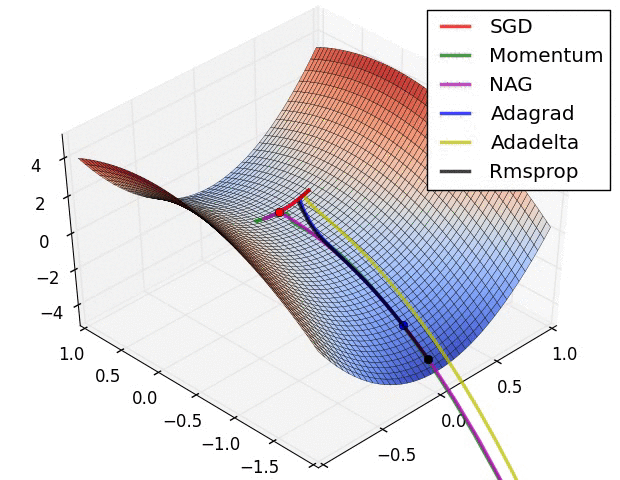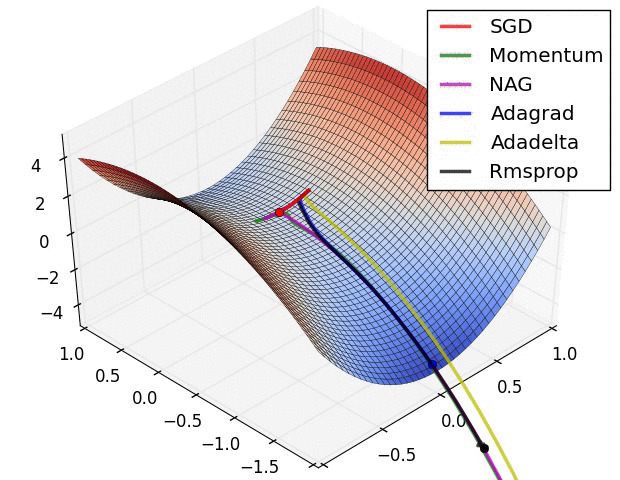
SGD，momentum，Nesterov momentum参数更新方法

Vanilla update：最简单的方法，往负梯度方向更新参数。

# Vanilla update
x += - learning_rate * dx

learning_rate学习率是一个超参数。

Momentum update：

Δxt=ρΔxt−1−η⋅gt

借鉴了物理中的惯性，把损失看成是凹凸不平的面，放一个小球，动量法就类似于小球在面上滚动。

# Momentum update
v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position

其中v初始值是0，mu是一个超参数，一般设为0.9，也可以通过交叉验证从 [0.5, 0.9, 0.95, 0.99]中选取，从上面的迭代过程中我们可以看到，相对于传统的沿梯度方向更新的方法，这里的更新是在之前的基础上的更新，如果最后dx变为0，经过多次乘以mu之后v也会变得非常小，也就是最后的停车，它保留了自然界中的惯性的成分，因此不容易在局部最优解除停止，而且中间有加速度所以会加速运算的过程。

Nesterov Momentum：动量法的改进版本，在凸函数收敛上有很好的理论保证，实际使用也比标准的动量法稍微好一点。之前我们采用 v=mu∗v−learningrate∗dx 的方法计算增量，其中的dx还是当前的x，但是我们已经知道了，下一刻的惯性将会带我们去的位置，所以现在我们要用加了mu*v之后的x，来更新位置，下面的图很形象：

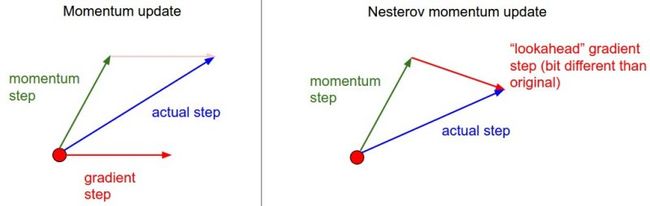
x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v

用类似于前面SGD和动量的方法更新：

v_prev = v # back this up
v = mu * v - learning_rate * dx # velocity update stays the same
x += -mu * v_prev + (1 + mu) * v # position update changes form

Annealing the learning rate学习率衰减

在训练网络的时候，将学习速率进行退火衰减处理，一般会有些帮助。学习率衰减太快，会浪费太多时间，衰减太慢曲线波动大，而且达不到最优点。一般有3种衰减方法：

1. 按步衰减（Step decay）：每多少epoch减小学习率，典型的值是5epoch减小一半，或者20epoch减小0.1，主要取决于问题和模型的类型。以固定学习率训练，如果看到验证集误差停止提升，就可以减小学习率，比如说减小一半
2. 指数衰减（Exponential decay）： α=α0e−kt ， α0,k 是超参数，t是迭代次数（或者epoch）
3. 1/t衰减： α=α0/(1+kt) ，参数同2

1比较多一点，因为超参数可以解释。如果有足够的资源，学习率可以小一点训练更多时间。

Second order methods

Second order methods是基于牛顿法的二次方法，它的迭代公式如下：

x←x−[Hf(x)]−1∇f(x)

其中, Hf(x)是Hessian matrix黑塞矩阵. 他是二阶偏导数构成的方阵∇f(x)是梯度向量, 引入海森矩阵的逆阵可以使得在坡度陡时候减小学习步伐，坡度缓的时候加快学习步伐 ，值得注意的是这种方法并不涉及学习速率的超参数，这是相对于一阶方法 first-order methods的优势。

可是，hessian矩阵的计算成本太高，深度学习中的网络有比较大，如果有100万个参数，海森矩阵的size为 [1,000,000 x 1,000,000], 需要3725G的RAM.
虽然现在有近似于hessian矩阵的方法例如L-BFGS,但是它需要在整个训练集中进行训练, 这也使得L-BFGS or similar second-order methods等方法在大规模学习的今天不常见的原因。如何是l-bfgs能像sgd一样在mini-batches上比较好的应用也是现在一个比较热门的研究领域。

自适应调整学习率的方法

前面的方法有的是通过别的超参数来调整学习率，以下几种是自适应调整学习率的方法

Adagrad：借鉴L2正则化，只是不是调节W，而是梯度。

Δxt=−η∑tτ=1(gτ)2−−−−−−−−√⋅gt

注意到cache与梯度矩阵同形，他是一个针对每个参数的梯度迭代累加的矩阵，他作为分母可以使在梯度大的时候学习效率速率降低，梯度小的时候学习速率增高，要注意的是开根号很重要的，没了他效果会大打折扣。

# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

其中eps一般取值1e-4 到1e-8，以避免分母出现0。但是这种方法用在深度学习中往往会学习的波动较大，并且使过早的停止学习。

RMSprop：Adagrad的改进，通过移动平均来减小波动。

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

改变就是分母中的cache，其中decay_rate是一个超参数，典型取值是[0.9, 0.99, 0.999]。cache的改变使这种方法有adagrad根据参数梯度自调整的优点，也克服adagrad单调减小的缺点。

Adam：有点像RMSProp+momentum

简单实现

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

论文中推荐eps = 1e-8, beta1 = 0.9, beta2 = 0.999. 完整版的程序还包括了一个偏差修正值，以弥补开始时m,v初始时为零的现象。

实际使用中，推荐Adam，他会比RMSProp效果好些. 也可以尝试SGD+Nesterov Momentum。另外如果能够允许全局的更新时可以试试L-BFGS。

更新版本，一般是用这个

# t is your iteration counter going from 1 to infinity
m = beta1*m + (1-beta1)*dx
mt = m / (1-beta1**t)
v = beta2*v + (1-beta2)*(dx**2)
vt = v / (1-beta2**t)
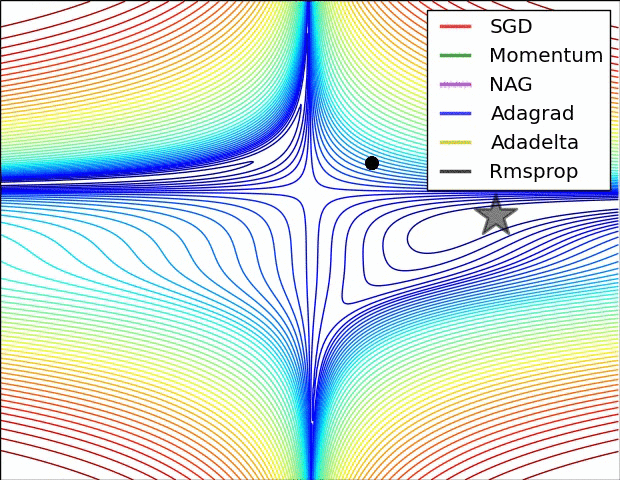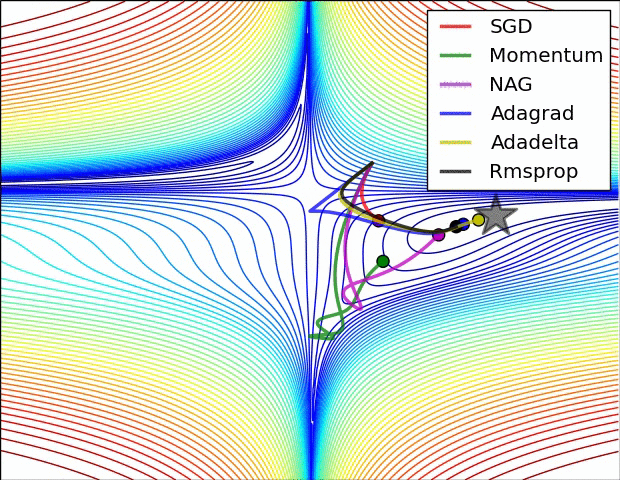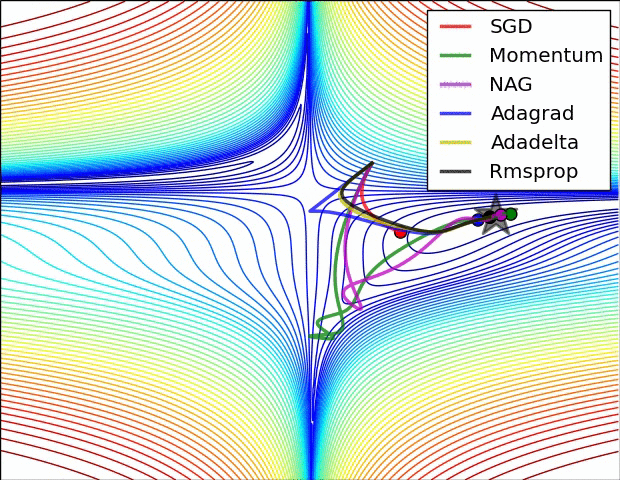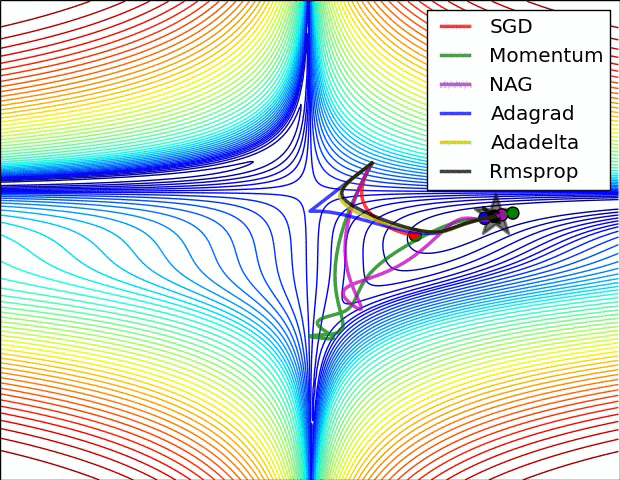
x += - learning_rate * mt / (np.sqrt(vt) + eps)

各种方法比较

超参数优化

常见的超参数：

1. 初始学习速率
2. 学习速率衰减策略（例如衰减系数）
3. 正则项比例（L2正则，dropout）

还有其他很多相对不敏感的超参数，例如参数自适应学习方法、动量及其策略的设置。下面介绍一些超参数搜索的注意点：

1. 大规模的网络需要很长时间训练，因此超参数搜索需要数天或者星期时间。在设计程序的时候需要注意两个模块，第一是能够保存超参数和性能，在训练阶段，能够追踪每epoch验证集性能的变化，保存在模型的检查点中；其二是在集群中能够调度模块1，能够检查模块1的检查点和绘制训练数据等
2. 只需要在一个验证集进行交叉验证，不需要“折”。（因为数据集大，所以验证集数据足够完成评估的任务？）
3. 超参数范围。使用log尺度搜索超参数。一个典型的例子就是学习率。learning_rate = 10 ** uniform(-6, 1)，因为学习率如果是0.9-0.99，选中0.9-0.91和0.98-0.99的概率是一样的，但是我们想在0.98-0.99概率更大一点，就用到了对数尺度。有些参数（比如dropout）就不需要这个（dropout = uniform(0,1)）
4. 随机搜索比网格搜索效率更高
5. 注意超参数范围边界的值是不是最优值
6. 现在一个大的范围搜索，然后缩小范围。可以先训练一个epoch看看效果，因为有的参数设置会直接让模型停止学习，然后缩小范围训练5epochs，最后在更精确的范围搜素更多的epochs
7. 利用Bayesian方法进行超参数优化。很多人在探究，现在已经有了一些工具箱比如Spearmint, SMAC, 及Hyperopt.但是在 ConvNets 上表现还是不如给定间隔的随机选择

模型集成

在测试阶段，综合一些神经网络的结果，来提高性能。模型越多样，提升效果越好。

1. 不同初始值的同一个模型。用交叉验证确定最好的超参数以后，设置不同的初始值得到不同的模型
2. 在交叉验证确定最优超参数的时候，挑选前几个（10）模型来构成集成。这种方法提高了模型多样性，但是可能会带入一些参数次优的模型。实际中这种方法容易使用，因为不需要额外的再训练
3. 一个模型的不同检查点。如果训练代价太大，那么就可以用这种。虽然缺少了模型多样性，但是用起来还算好，而且成本低
4. 平均训练参数。另外一个比较容易得到的模型就是copy下网络的参数，然后用指数下降的方式求训练过程中的平均，最终得到了最后几次迭代为主的模型，这样的模型经常会有些比较好的表现。一种直观的解释是在一个碗状的目标函数，我们得到结果经常在最下方的附近进行跳跃，而用平均值就会增加了更接近碗底的机会

模型集成的缺点是在测试集上太耗时。

完成Softmax和一个简单的神经网络

http://cs231n.github.io/neural-networks-case-study/

参考资料

1. 视频课程地址
2. 官方资料网站
3. 课后作业参考
4. 神经网络激活函数
5. 训练深度神经网络尽量使用zero-centered数据
6. Vectorized、PCA和Whitening
7. 讲义总结：梯度检验 参数更新 超参数优化 模型融合博客
8. 参数更新方法博客
9. Batch Normalization论文地址
10. 论文的中文整理博客