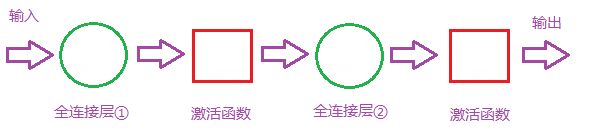
全连接层（Fully Connected Layer）

CNN 入门讲解：什么是全连接层（Fully Connected Layer）?

 

 

新年第一更

祝大家新年快乐万事如意

这个时候还愿意点进来，新的一年肯定要起飞了

 

这情人节和新年连着过啊

这对情侣意味着什么，意味着要带情人去见家长了

当然对一些情侣意味着，情人节过不好，估计年也过不好

 

对于那些没用男女朋友的，不要心急，不要灰心

好好学习，好好生活，站直走路背影要美

总有一个人愿意跨过所有时间来到你身边

可能ta步履蹒跚，衣衫不整

但你一定要以最帅/美的姿态迎接ta

 

那些过年没回家的

也不要失望

心中有方向

哪怕整个世界阻拦你

你都会回家的

 

我来教大家放个烟花

----------------------------------------- _φ_(．．) 正文开始--------------------------------------------

微信公号：follow_bobo

首发于专栏卷积神经网络（CNN）入门讲解

时隔一个月，我又来更新啦

啦啦啦

可能有很多小伙伴已经不满了

你怎么更新这么慢啊

其实不是的，其实我很多已经写好了

但是出于神秘原因，不能发

为什么不能发，以后你们就知道了

 

--------------------------------------好吧，正文现在才开始-----------------------------------------------------

 

 

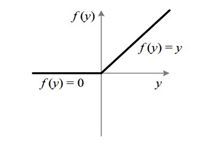
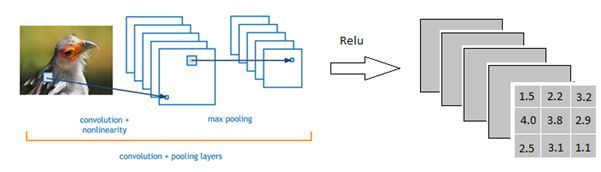
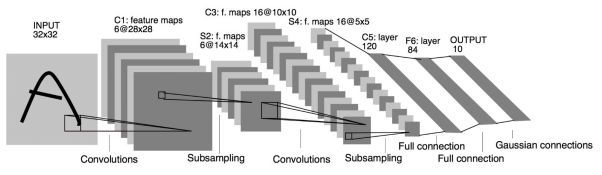
上一期我们讲到激活函数（Activation Function）,假设我们经过一个Relu之后的输出如下

Relu:

 

 

然后开始到达全连接层

啊啊啊，终于开始进入CNN的末尾了

已经推到敌军老家了，准备开始攻打水晶了

大家坚持住，黎明前，最黑暗

 

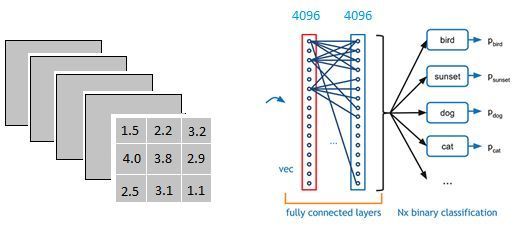
以上图为例，我们仔细看上图全连接层的结构，全连接层中的每一层是由许多神经元组成的（1x 4096）的平铺结构，上图不明显，我们看下图

 

注：上图和我们要做的下面运算无联系

并且不考虑激活函数和bias

 

 

 

当我第一次看到这个全连接层，我的第一个问题是：

 

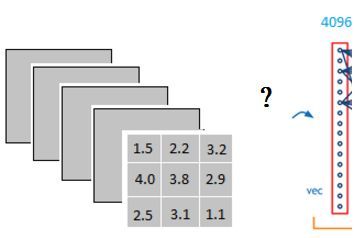
它是怎么样把3x3x5的输出，转换成1x4096的形式

 

 

 

 

很简单,可以理解为在中间做了一个卷积

 

 

从上图我们可以看出，我们用一个3x3x5的filter 去卷积激活函数的输出，得到的结果就是一个fully connected layer 的一个神经元的输出，这个输出就是一个值

因为我们有4096个神经元

我们实际就是用一个3x3x5x4096的卷积层去卷积激活函数的输出

以VGG-16再举个例子吧

再VGG-16全连接层中

对224x224x3的输入，最后一层卷积可得输出为7x7x512，如后层是一层含4096个神经元的FC，则可用卷积核为7x7x512x4096的全局卷积来实现这一全连接运算过程。

很多人看到这，可能就恍然大悟

哦，我懂了，就是做个卷积呗

不

你不懂

 

敲黑板了

麻烦后排吃东西的同学叫下前排玩游戏的同学去把第一排的同学吵醒

我要说重点了！！！！！！！！！！！

 

这一步卷积一个非常重要的作用

就是把分布式特征representation映射到样本标记空间

什么，听不懂

那我说人话

就是它把特征representation整合到一起，输出为一个值

 

这样做,有一个什么好处？

就是大大减少特征位置对分类带来的影响

 

 

来，让我来举个简单的例子

 

 

这个例子可能过于简单了点

可是我懒得画了，大家将就着看吧

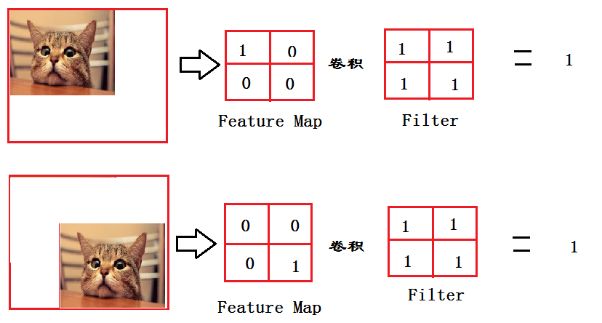
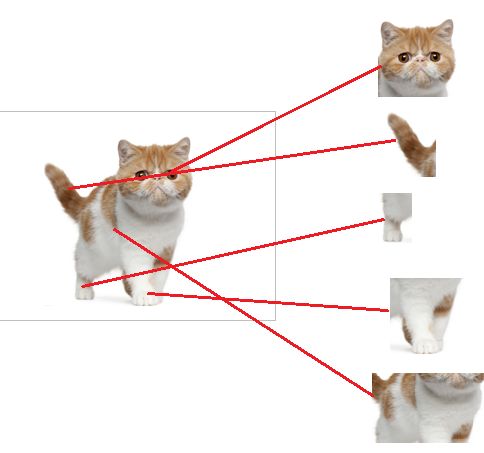
从上图我们可以看出，猫在不同的位置，输出的feature值相同，但是位置不同

对于电脑来说，特征值相同，但是特征值位置不同，那分类结果也可能不一样

而这时全连接层filter的作用就相当于

喵在哪我不管

我只要喵

于是我让filter去把这个喵找到

实际就是把feature map 整合成一个值

这个值大

哦，有喵

这个值小

那就可能没喵

和这个喵在哪关系不大了有没有

鲁棒性有大大增强了有没有

喵喵喵

 

因为空间结构特性被忽略了，所以全连接层不适合用于在方位上找Pattern的任务，比如segmentation

 

 

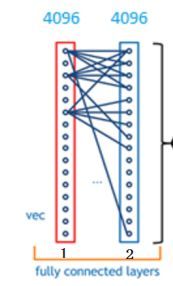
ok, 我们突然发现全连接层有两层1x4096fully connected layer平铺结构(有些网络结构有一层的，或者二层以上的)

好吧也不是突然发现，我只是想增加一点戏剧效果

 

 

 

但是大部分是两层以上呢

这是为啥子呢

 

泰勒公式都知道吧

意思就是用多项式函数去拟合光滑函数

我们这里的全连接层中一层的一个神经元就可以看成一个多项式

 

我们用许多神经元去拟合数据分布

但是只用一层fully connected layer 有时候没法解决非线性问题

而如果有两层或以上fully connected layer就可以很好地解决非线性问题了

 

说了这么多，我猜你应该懂的

听不懂？

那我换个方式给你讲

 

 

我们都知道，全连接层之前的作用是提取特征

全理解层的作用是分类

我们现在的任务是去区别一图片是不是猫

 

哈哈哈，猫猫好可爱

我先撸一把先

 

撸完了，回来啦（嗯，怎么好像哪里不对）

 

假设这个神经网络模型已经训练完了

全连接层已经知道

 

当我们得到以上特征，我就可以判断这个东东是猫了

 

 

因为全连接层的作用主要就是实现分类（Classification）

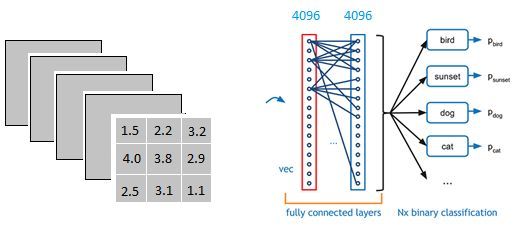
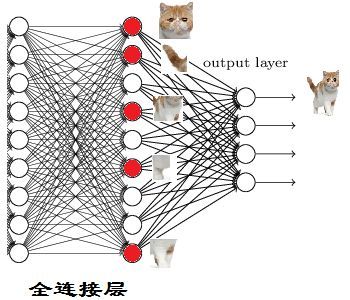
从下图，我们可以看出

 

 

红色的神经元表示这个特征被找到了（激活了）

同一层的其他神经元，要么猫的特征不明显，要么没找到

当我们把这些找到的特征组合在一起，发现最符合要求的是猫

ok，我认为这是猫了

那我们现在往前走一层

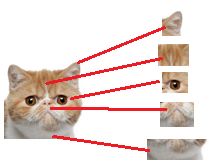
那们现在要对子特征分类，也就是对猫头，猫尾巴，猫腿等进行分类

比如我们现在要把猫头找出来

 

猫头有这么些个特征

于是我们下一步的任务

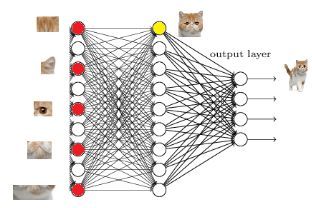
就是把猫头的这么些子特征找到，比如眼睛啊，耳朵啊

 

道理和区别猫一样

当我们找到这些特征，神经元就被激活了（上图红色圆圈）

这细节特征又是怎么来的？

就是从前面的卷积层，下采样层来的

 

至此，关于全连接层的信息就简单介绍完了

 

全连接层参数特多（可占整个网络参数80%左右），近期一些性能优异的网络模型如ResNet和GoogLeNet等均用全局平均池化（global average pooling，GAP）取代全连接层来融合学到的深度特征

需要指出的是，用GAP替代FC的网络通常有较好的预测性能

于是还出现了

[1411.4038] Fully Convolutional Networks for Semantic Segmentation​arxiv.org

 

以后会慢慢介绍的
----------------------------------------------------------------------------------------------

说实话，说的有点简单

但是我不能摆公式啊

不能摆计算啊

所以

大家就将就着看吧

有问题在下面留言

 

 

 

-------------------------------------------------------------------

新年快乐啦

有人说以前的文风太浮夸

现在我严谨一些

不知道大家喜欢不

喜欢的

点个赞

---

问题汇总简答（持续更新）：

（1）全连接层对模型的影响？

首先我们明白全连接层的组成如下：

二层全连接层结构

那么全连接层对模型影响参数就是三个：

1. 全接解层的总层数（长度）
2. 单个全连接层的神经元数（宽度）
3. 激活函数

首先我们要明白激活函数的作用是：

增加模型的非线性表达能力

更详细了解请去：

蒋竺波：CNN入门讲解：什么是激活函数（Activation Function）​zhuanlan.zhihu.com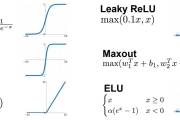

 

如果全连接层宽度不变，增加长度：

优点：神经元个数增加，模型复杂度提升；全连接层数加深，模型非线性表达能力提高。理论上都可以提高模型的学习能力。

如果全连接层长度不变，增加宽度：

优点：神经元个数增加，模型复杂度提升。理论上可以提高模型的学习能力。

难度长度和宽度都是越多越好？

肯定不是

（1）缺点：学习能力太好容易造成过拟合。

（2）缺点：运算时间增加，效率变低。

那么怎么判断模型学习能力如何？

看Training Curve 以及 Validation Curve，在其他条件理想的情况下，如果Training Accuracy 高， Validation Accuracy 低，也就是过拟合 了，可以尝试去减少层数或者参数。如果Training Accuracy 低，说明模型学的不好，可以尝试增加参数或者层数。至于是增加长度和宽度，这个又要根据实际情况来考虑了。

PS：很多时候我们设计一个网络模型，不光考虑准确率，也常常得在Accuracy/Efficiency 里寻找一个好的平衡点。

 

 

麻烦大家给我点个赞，就是那种让我看起来，写的还不错的样子!

拜托了！！o(´^｀)o