人工神经网络笔记(一)后向传播、随机最优化、设定超参数
人工神经网络笔记(一)后向传播、随机最优化、设定超参数
- Background propagation
- Stochastic optimization
- Hyper-parameter tuning
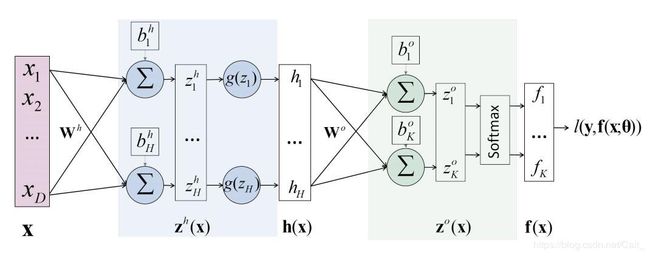
1、一个简单的神经网络
其中, l ( y , f ( x : θ ) l(y,f(x: \theta) l(y,f(x:θ) 代表损失函数,表示真实值和预测值之间的差距,模型参数 θ = [ W h , W o , b h , b o ] \theta =[W^h,W^o,b^h,b^o] θ=[Wh,Wo,bh,bo] ;
该神经网络的目标是找到使得 l l l最小的 θ \theta θ
后向传播(Background propagation):利用链式法则计算梯度,再更新模型参数;
例,对于 w 1 w_1 w1
δ l δ w 1 = δ l δ h 1 δ h 1 δ w 1 = ( δ l δ z 1 δ z 1 δ h 1 + δ l δ z 2 δ z 2 δ h 1 ) ∗ ( δ h 1 δ u 1 δ u 1 δ w 1 ) \frac{\delta l}{\delta w_1} = \frac{\delta l}{\delta h_1} \frac{\delta h_1}{\delta w_1} = (\frac{\delta l}{\delta z_1}\frac{\delta z_1}{\delta h_1}+\frac{\delta l}{\delta z_2}\frac{\delta z_2}{\delta h_1} )*(\frac{\delta h_1}{\delta u_1}\frac{\delta u_1}{\delta w_1}) δw1δl=δh1δlδw1δh1=(δz1δlδh1δz1+δz2δlδh1δz2)∗(δu1δh1δw1δu1)
w 1 = w 1 − l r ∗ δ l δ w 1 w_1 = w_1 - lr*\frac{\delta l}{\delta w_1} w1=w1−lr∗δw1δl
l r 表 示 学 习 率 lr表示学习率 lr表示学习率
2、梯度下降法
2.1 Batch gradient descant
θ t + 1 = θ t − η ∇ L ( θ t ) = θ t − η N ∑ n = 0 N ∇ l ( y n , f ( x n : θ t ) ) \theta_{t+1} = \theta_t - \eta\nabla L(\theta_t) = \theta_t - \frac{\eta}{N}\sum^N_{n=0} \nabla l(y_n,f(x_n:\theta_t)) θt+1=θt−η∇L(θt)=θt−Nη∑n=0N∇l(yn,f(xn:θt))
缺点:每次训练都使用全部训练样本,导致训练过程缓慢,且对内存要求大;
优点:能找到损失函数的最小值;
2.2 Stochastic gradient descent
θ t + 1 = θ t − η ∇ L ( θ t ) = θ t − η ∇ l ( y n , f ( x n : θ t ) ) \theta_{t+1} = \theta_t - \eta\nabla L(\theta_t) = \theta_t - \eta \nabla l(y_n,f(x_n:\theta_t)) θt+1=θt−η∇L(θt)=θt−η∇l(yn,f(xn:θt))
缺点:存在收敛波动
优点
(1)每次使用一个样本进行更新,更新速度快;
(2)可能学习到更好的局部最优解;
2.3 Mini-batch gradient descent
θ t + 1 = θ t − η ∇ L ( θ t ) = θ t − η ∣ S ∣ ∑ ( x n , y n ) ∈ S ∇ l ( y n , f ( x n : θ t ) ) \theta_{t+1} = \theta_t - \eta\nabla L(\theta_t) = \theta_t - \frac{\eta}{|S|} \sum_{(x_n,y_n) \in S} \nabla l(y_n,f(x_n:\theta_t)) θt+1=θt−η∇L(θt)=θt−∣S∣η∑(xn,yn)∈S∇l(yn,f(xn:θt))
每次迭代选取一个批量的数据,|S|通常取10-300的范围,综合了Batch和 Stochastic两种方法的优点;
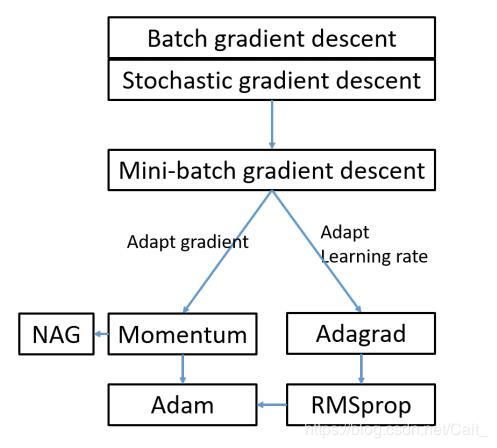
3 优化梯度的下山法
3.1 Momentum
可以理解为:在下降过程中,之前的下降冲量还具有残存的影响,有时这种影响能帮助度过滑坡;
v t + 1 = γ v t + η ∇ L ( θ t ) v_{t+1} = \gamma v_t + \eta \nabla L(\theta_t) vt+1=γvt+η∇L(θt)
θ t + 1 = θ t − v t + 1 \theta_{t+1} = \theta_t - v_{t+1} θt+1=θt−vt+1
其中, γ \gamma γ是衰减率,那么迭代地,可以有:
v t + 1 = η ( ∇ L ( θ t ) + γ ∇ L ( θ t − 1 ) + γ 2 ∇ L ( θ t − 2 ) + . . . . . . ) v_{t+1} = \eta (\nabla L(\theta_t) + \gamma \nabla L(\theta_{t-1}) + \gamma^2 \nabla L(\theta_{t-2}) + ......) vt+1=η(∇L(θt)+γ∇L(θt−1)+γ2∇L(θt−2)+......)
简单理解为:在每次下降过程中,下降方向的选取由当前梯度和之前的梯度共同决定;
3.2 Nesterov accelerated gradient(NAG)
考虑未来下降的位置: θ − γ v t \theta - \gamma v_t θ−γvt,当前下降方向由当前位置和未来位置共同决定:
v t + 1 = γ v t + η ∇ L ( θ t − γ v t ) v_{t+1} = \gamma v_t + \eta \nabla L(\theta_t - \gamma v_t) vt+1=γvt+η∇L(θt−γvt) ,
θ t + 1 = θ t − v t + 1 \theta_{t+1} = \theta_t - v_{t+1} θt+1=θt−vt+1
γ 代 表 衰 减 率 , η 代 表 学 习 率 ; \gamma 代表衰减率,\eta 代表学习率; γ代表衰减率,η代表学习率;
4 自适应学习率
4.1 Adagrad
使用历史梯度的平方和的平方根自适应地更新每个参数的学习速度;
历史导数平方和 g t , i g_{t,i} gt,i的递归表示形式:
g t + 1 , i = g t , i + ( ∂ L ( θ t ) ∂ θ i ) 2 g_{t+1,i} = g_{t,i} + {(\frac{\partial L(\theta_t)}{\partial \theta_i})}^2 gt+1,i=gt,i+(∂θi∂L(θt))2
自适应学习率的梯度更新方式:
θ t + 1 , i = θ t , i − η g t + 1 , i + ϵ ( ∂ L ( θ t ) ∂ θ i ) \theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{g_{t+1,i} + \epsilon}(\frac{\partial L(\theta_t)}{\partial \theta_i}) θt+1,i=θt,i−gt+1,i+ϵη(∂θi∂L(θt))
无需手动调整学习率,随着迭代时间的推移,历史梯度平方和会变大,最终导致学习率降低;
4.2 Root Mean Square propagation(RMSprop)
g t + 1 , i = γ g t , i + ( 1 − γ ) ( ∂ L ( θ t ) ∂ θ i ) 2 g_{t+1,i} = \gamma g_{t,i} + (1-\gamma) {(\frac{\partial L(\theta_t)}{\partial \theta_i})}^2 gt+1,i=γgt,i+(1−γ)(∂θi∂L(θt))2
θ t + 1 , i = θ t , i − η g t + 1 , i + ϵ ( ∂ L ( θ t ) ∂ θ i ) \theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{g_{t+1,i} + \epsilon}(\frac{\partial L(\theta_t)}{\partial \theta_i}) θt+1,i=θt,i−gt+1,i+ϵη(∂θi∂L(θt))
通常地, g a m m a = 0.9 , g t + 1 , i 是 梯 度 的 历 史 平 均 值 gamma = 0.9 , g_{t+1,i}是梯度的历史平均值 gamma=0.9,gt+1,i是梯度的历史平均值
4.3 Adaptive Moment Estimation
自适应矩估计, m t , i 代 表 一 阶 均 值 矩 , g t , i 代 表 二 阶 方 差 矩 m_{t,i}代表一阶均值矩,g_{t,i}代表二阶方差矩 mt,i代表一阶均值矩,gt,i代表二阶方差矩
m t + 1 , i = β 1 m t , i + ( 1 − β 1 ) ∂ L ( θ t ) ∂ θ i m_{t+1,i} = \beta_1 m_{t,i} + (1-\beta_1)\frac{\partial L(\theta_t)}{\partial \theta_i} mt+1,i=β1mt,i+(1−β1)∂θi∂L(θt)
m t + 1 , i ′ = m t + 1 , i 1 − β 1 t + 1 m_{t+1,i}^{'} = \frac{m_{t+1,i}}{1-\beta_1^{t+1}} mt+1,i′=1−β1t+1mt+1,i
g t + 1 , i = β 2 g ( t , i ) + ( 1 − β 2 ) ( ∂ L ( θ t ) ∂ θ i ) 2 g_{t+1,i} = \beta_2 g(t,i) + (1 - \beta_2){(\frac{\partial L(\theta_t)}{\partial \theta_i})}^2 gt+1,i=β2g(t,i)+(1−β2)(∂θi∂L(θt))2
g t + 1 , i ′ = g t + 1 , i 1 − β 2 t + 1 g_{t+1,i}^{'} = \frac{g_{t+1,i}}{1-\beta_2^{t+1}} gt+1,i′=1−β2t+1gt+1,i
θ t + 1 , i = θ t , i − η g t + 1 , i ′ + ϵ m t + 1 , i ′ \theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{g_{t+1,i}^{'} + \epsilon} m_{t+1,i}^{'} θt+1,i=θt,i−gt+1,i′+ϵηmt+1,i′
5 总结
6 附:Hyper-parameter tuning
6.1 超参数训练
超参数:在机器学习中,超参数是指预先设置的参数,而不是通过训练得到的参数,例如:学习率lr、神经网络层数、神经元数量等;
将数据集分为三部分:
(1)Training set:训练集,训练模型参数;
(2)Validation set:验证集,训练超参数;
(3)Test set:测试集,模型验证;
在经过训练的模型中,选择在验证集上具有最佳性能的一组超参数;
问:多组超参数从何而来?
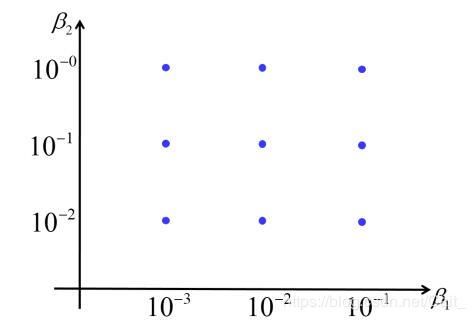
(1)Grid Search(网格搜索)
在参数空间内的穷举搜索,只适用于小量的超参数;
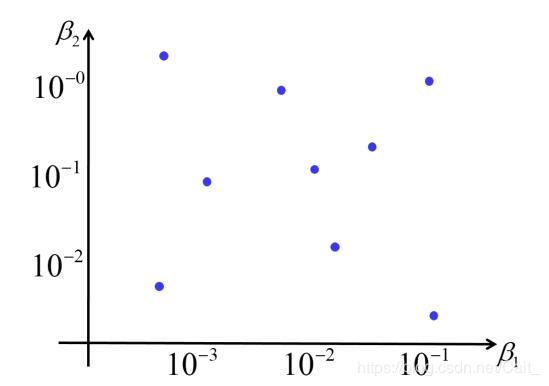
(2)Random Search(随机搜索)
当参数数量较多时,优于网格搜索;
(3)超参数训练过程中的进化策略:类似于遗传算法,结合最好与最坏的超参数集,通过交叉和变异,获取新的超参数集;
6.2 训练与验证
当训练集合较小时,使用K-交叉验证,(K-1)份训练集,1份测试集;