【UVA10256】The Great Divide（凸包相离判定）

提交地址：

题目：

---

pdf：https://uva.onlinejudge.org/external/102/10256.pdf

n个红点，m个蓝点，是否存在一条直线，使得任取一个红点和一个蓝点都在直线的异侧？这条直线不能穿过红点或者蓝点

 

解题思路：

---

先求出红点和蓝点的凸包，如果这两个凸包是相离的，那么一定能找到一个满足条件的直线，问题转化为判断两个凸包是否相离。

（1）任取一个红点（或者蓝点），如果这个红点（或者蓝点）都不在那一个凸包内（点在多边形内判定）， 那么这两个凸包有可能相离。

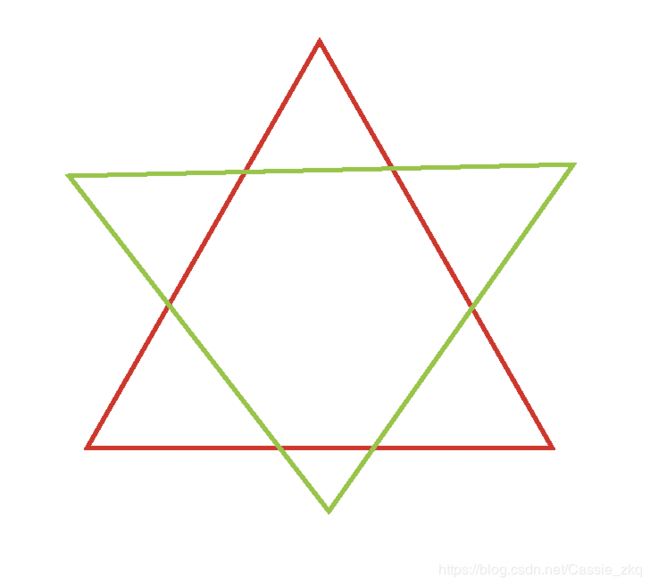
（2）光满足条件（1）还不够，因为可能会出现下图这样的情况，所以还需要判断两个凸包的任意两条边之间是否相交。

（3）当凸包是一个点或者线段需要特判。

 

ac代码：

---

#include 
using namespace std;
const double pi = acos(-1.0);
const double eps = 1e-6;
const int maxn = 550;
int dcmp(double x)//精度三态函数(>0,<0,=0)
{
    if (fabs(x) < eps)return 0; //等于
    else return x < 0 ? -1 : 1;//小于，大于
}
struct Point{
    double x, y;
    Point(double x = 0, double y = 0):x(x),y(y){}
    friend bool operator == (Point a, Point b)
    {
        return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0;
    }
    friend bool operator < (Point a, Point b)
    {
        return a.x == b.x ? a.y < b.y : a.x < b.x;
    }
};
typedef Point Vector;

Vector operator - (Vector a, Vector b)//向量减法
{
    return Vector(a.x - b.x, a.y - b.y);
}

double Dot(Vector a, Vector b)//点积
{
    return a.x * b.x + a.y * b.y;
}
double Cross(Vector a, Vector b)//外积
{
    return a.x * b.y - a.y * b.x;
}


bool Onsegment(Point p, Point a1, Point a2)
{
    return dcmp(Cross(a1 - p, a2 - p)) == 0 && dcmp(Dot(a1 - p, a2 - p)) < 0;
}
bool JudgeSegmentIntersect(Point A, Point B, Point C, Point D) //线段相交（包括端点）
{
    return
            dcmp(max(A.x, B.x) - min(C.x, D.x)) >= 0
            && dcmp(max(C.x, D.x) - min(A.x, B.x)) >= 0
            && dcmp(max(A.y, B.y) - min(C.y, D.y)) >= 0
            && dcmp(max(C.y, D.y) - min(A.y, B.y)) >= 0
            && dcmp(Cross(C - A, D - A)*Cross(C - B, D - B)) <= 0
            && dcmp(Cross(A - C, B - C)*Cross(A - D, B - D)) <= 0;
}

int isPointInPolygon(Point p, Point v[], int n)//n多边形顶点个数
{
    int wn = 0;
    for(int i = 0; i < n; i++)//多边形的端点从0开始存
    {
        if(Onsegment(p, v[i], v[(i+1)%n])) return -1;//在边界上
        int k = dcmp(Cross(v[(i+1)%n] - v[i], p-v[i]));
        int d1 = dcmp(v[i].y - p.y);
        int d2 = dcmp(v[(i+1)%n].y - p.y);
        //后两个条件确保射线能穿过多边形的这条边
        if(k>0 && d1<=0 && d2>0) wn++;//p在v[i]和v[(i+1)%n]向量左侧且y值在[v[i].y,v[(i+1)%n.y)
        if(k<0 && d2<=0 && d1>0) wn--;//右侧，且[v(i+1)%n.y, v[i].y)
    }
    if(wn!=0) return 1;//内部
    return 0;//外部
}

int ConvexHull(Point *p, int n, Point* ch)//凸包,ch存结果
{
    sort(p, p+n);//先x后y
    int m = 0;//ch存最终的凸包顶点，下标从0开始
    for(int i = 0; i < n; i++)
    {
        //m是待确定的
        while(m > 1 && dcmp(Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2])) <= 0) m--;
        ch[m++] = p[i];
    }
    int k = m;
    for(int i = n-2; i >= 0; i--)
    {
        while(m > k && dcmp(Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2])) <= 0) m--;//同样的方向
        ch[m++] = p[i];
    }
    if(n>1) m--;//m是凸包上的点数+1，相当于n，ch[m]和ch[0]相同，遍历的时候 2) return !isPointInPolygon(ch1[0], ch2, m2);
    else if(m2 == 1 && m1 > 2) return !isPointInPolygon(ch2[0], ch1, m1);
    else if(m1 == 2 && m2 > 2)
    {
        for(int i = 0; i < m2; i++)
            if(JudgeSegmentIntersect(ch1[0], ch1[1], ch2[i], ch2[(i+1)%m2])) return false;//线段是否在另一个凸包的边上
        int d1 = isPointInPolygon(ch1[0], ch2, m2);
        if(d1 == -1 || d1 == 1) return false;
        int d2 = isPointInPolygon(ch1[1], ch2, m2);
        if(d2 == -1 || d2 == 1) return false;
        return true;
    }
    else if(m2 == 2 && m1 > 2)
    {
        for(int i = 0; i < m1; i++)
            if(JudgeSegmentIntersect(ch2[0], ch2[1], ch1[i], ch1[(i+1)%m1])) return false;
        int d1 = isPointInPolygon(ch2[0], ch1, m1);
        if(d1 == -1 || d1 == 1) return false;
        int d2 = isPointInPolygon(ch2[1], ch1, m1);
        if(d2 == -1 || d2 == 1) return false;
        return true;
    }
    else//m1>2 m2>2
    {
        for(int i = 0; i < m1; i++)
            for(int j = 0; j < m2; j++)
                if(JudgeSegmentIntersect(ch1[i], ch1[(i+1)%m1], ch2[j], ch2[(j+1)%m2])) return false;
        for(int i = 0; i < m1; i++)
        {
            int d = isPointInPolygon(ch1[i], ch2, m2);
            if(d == -1 || d == 1) return false;
        }
        for(int i = 0; i < m2; i++)
        {
            int d = isPointInPolygon(ch2[i], ch1, m1);
            if(d == -1 || d == 1) return false;
        }
        return true;
    }

}
int main()
{
    //freopen("/Users/zhangkanqi/Desktop/11.txt","r",stdin);
    while(scanf("%d %d",&n, &m))
    {
        if(n == 0 && m == 0) break;
        for(int i = 0; i < n; i++) scanf("%lf %lf", &p1[i].x, &p1[i].y);
        for(int i = 0; i < m; i++) scanf("%lf %lf", &p2[i].x, &p2[i].y);
        m1 = ConvexHull(p1, n, ch1);
        m2 = ConvexHull(p2, m, ch2);
        if(check()) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}