关于python快速求正整数幂的研究

一直以来，快速求幂屡屡出现在各种题目中（内置pow直接返回？），虽然关于python实现快速求幂可能有很多版本，大部分基于原始C语言版本的生硬的python版本，我也背过一本《高效算法》里的快速求幂，然而其趋向C过于严重，以至于过不了多久全然忘记，或者可操作性极差，需要反复翻阅，难得求职期间闲暇，故对于python版本的快速求正整数幂稍作研究。

《高效算法》版本:

def fast_exponentiation(a, b, q):
    assert a >= 0 and b >= 0 and q >= 1
    p = 0  # 只用于记录
    p2 = 1  # 2^p
    ap2 = a % q  # a^(2^p)
    result = 1
    while b > 0:
        if p2 & b > 0:  # b由a^(2^p)拆分而来
            b -= p2
            result = (result * ap2) % q
        p += 1
        p2 *= 2
        ap2 = (ap2 * ap2) % q
    return result

看不懂不要问我，自己翻书去，在下也是难以记住，类C的Python算法真正做到了只是换了语法，估计改写成C都不用费多少力气

内置函数版本：

def pow(*args, **kwargs): # real signature unknown
    """
    Equivalent to x**y (with two arguments) or x**y % z (with three arguments)
    
    Some types, such as ints, are able to use a more efficient algorithm when
    invoked using the three argument form.
    """
    pass

这里就不做过多解释了，下面才是我自己总结的一些东西：

装饰器+递归版本：

import functools


def memoize(fn):
    know = {}

    @functools.wraps(fn)
    def memoizer(*args):
        if args not in know:
            know[args] = fn(*args)
        return know[args]

    return memoizer


@memoize
def quick_pow(base, n):  # 正整数快速求幂
    """省去合法性检查"""
    if n == 0:
        return 1
    if n % 2 == 0:
        return quick_pow(base, n // 2) * quick_pow(base, n // 2)
    else:
        return quick_pow(base, (n - 1) // 2) * quick_pow(base, (n - 1) // 2) * base

话不多说，时间复杂度分析讲起来太累，听者大多也自动过滤，这里采用实例分析，Timer函数直观给出数据：

if __name__ == '__main__':
    from timeit import Timer

    t1 = Timer('fast_exponentiation(10,1000,1000000000)', 'from __main__ import fast_exponentiation')
    t2 = Timer('pow(10,1000)')
    t3 = Timer('quick_pow(10,1000)', 'from __main__ import quick_pow')
    print(t1.timeit())
    print(t2.timeit())
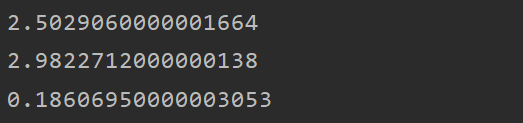
    print(t3.timeit())

结果如下：#分别对应文中算法顺序

也许有的读者发现算法1有三个参数，而测试时没有做好控制变量，实际上，第三个参数不存在的情况下，算法1测试结果更差，达到8.xxxx，有兴趣的读者可以自己测试。

不管是《高效算法》的算法1，还是这里的算法3，本质都是应用了幂的二进制，当然，这是很多书上或者资料上说的。而我的观点是，既然Python作为比C更抽象的语言，理应站在更高的层次，更抽象的模型解决问题，也即是更接近数学思维的方式解决此问题，算法3的本质是离散数学的递归和递推，基于以下一个递归式：

递归基 f(base,0)=1

f(base,n)=f(base,n/2)*f(base,n/2)  n为偶数

f(base,n)=f(base,(n-1)/2)*f(base,(n-1)/2)*base n为奇数

众所周知，这类递归很容易优化，一是改写成递推的形式，或者是记忆递归的方式，类似与斐波拉数。

递推和记忆递归各有特点，这里的算法3采用的是记忆递归的，并且采用Python的高级特性修饰器进行实现，以实现了几乎接近于原始递归式可读性，而且这个修饰器也是通用型记忆修饰器，几乎可以毫不修改地用于任何记忆递归算法。时间复杂度方面，算法1据说是O(log n)，算法2即内置pow函数时间复杂度也是O(log n)，实际测试快于算法1，算法3据我分析时间复杂度也为O(log n)，且系数低于前两个版本，实际测试速度最快。

当然，细心的读者肯定发现，算法3的高效也不是没有代价的，需要付出O(log n)的空间复杂度的代价，若非要O(1)空间复杂度算法3自然淘汰，但更宽松的情况下，我倒是更喜欢这种pythonic的优雅。