机器学习： 回归

Github

系列文章 pdf 版本已经上传至： https://github.com/anlongstory/awsome-ML-DL-leaning/tree/master/xiaoxiang-notes
欢迎 Star 和下载

前言

之前也有写过李航博士的《统计学习方法》的博客内容，即将书写的机器学习系列博客内容不可避免的要与之有所重叠，但是之前完成的 《统计学习方法》 系列的博客主要是对书中的一些概念的摘录（公式和图片大部分都是截取内容直接粘贴），旨在快速了解机器学习的相关概念，并没有一些拓展，本系列的文章更多的是想深入理解机器学习相关概念及背后的数学基础（为了更好的学习和阅读体验，数学公式推导都是一个个手打上去的，图片能自己代码生成也都是自己代码生成），主要脉络是跟着小象学院的机器学习视频走的，然后自己对整体的内容进行了取舍和整理，尽可能地有逻辑地呈现出来，帮助理解，因为水平有限，如果有错误还请留言指正。后面还会对本系列文章不定期代码部分内容，加深理解。

数学基础

在聊回归之前先了解一下基础的数学概念。

概率和似然

这两个概念都是指可能性

• 概率：给定某一参数值，求某一结果的可能性的函数
• 似然：给定某一结果，求某一参数值的可能性的函数

查阅资料的过程，最经典的就是抛硬币的例子，概率问题里，就是已知硬币正反面出现的概率各为 0.5，抛 10 次，6次正面向上的可能性是多少？而似然问题则是，抛 10 次硬币，有 6 次正面向上，求硬币正反面出现概率各为多少？

最大似然估计 MLE

继续上面抛硬币的问题，设正面向上的概率 $\theta$ , 所以反面出现的概率就是 $1-\theta$，因为本身情况已经是给定的，且每次抛硬币的实验是独立的，所以可以直接写出似然函数：
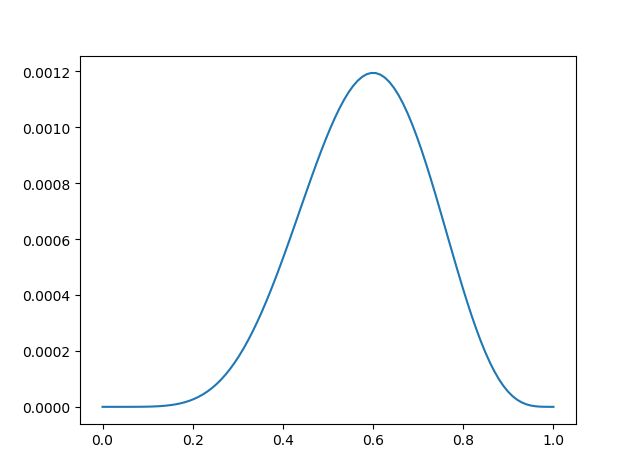
$$f\left(\theta \right)={\theta }^6{\left(1-\theta \right)}^4$$
我们画出这个函数的曲线可以看到：

当 $\theta$ 值为 0.6 时，函数 $f\left(\theta \right)$ 可以取得最大值。在求解 $f\left(\theta \right)$ 在 $\theta$ 为何值时最大的过程就是最大似然估计。

（在 ML 中，似然函数都是指数形式的，所以更多的做法是先取 log 简化表达式，然后再求最大似然估计 ）

最小二乘法

百度百科给出的定义是： 最小二乘法是通过最小化误差的平方和寻找数据的最佳函数匹配。

首先这里的关键词就是“误差的平方和”，我们可以用公式：

$$Error=\sum {\left(y-y_i\right)}^2$$

(1)

来表示相关上述概念，其中 $y$ 表示的预测值，$y_i$ 表示的是已知的真实值，$y_i$ 是固定的，我们可以通过调整 $y$ 的值来达到最后 $Error$ 最小，这样一个寻找预测值 $y$ 的过程就是最小二乘法的思想。

假设现在我们有 4 个样本点 $y_1,y_2,y_3,y_4$, 预测值为 $y$， 根据最小二乘法的定义，想要最后的 $Error$ 最小，我们需要对函数二次求导以后，求使导数为 0 的点，即：

$$\frac{\mathrm{d}\sum {\left(y-y_i\right)}^2}{\mathrm{d}y}=2\sum \left(y-y_i\right)=2\left(\left(y-y_1\right)+\left(y-y_2\right)+\left(y-y_3\right)+\left(y-y_4\right)\right)=0$$

(2)

化简上面的式子可以得到：
$$4y=y_1+y_2+y_3+y_4\Rightarrow y=\frac{y_1+y_2+y_3+y_4}{4}$$
这里的结果不就是算术平均值 $\bar{y}$ 么。

高斯分布

前面最小二乘法提到,对每一个预测值和真实值之间都会有一个误差 ${ϵ}_i$：
$${ϵ}_i=y-y_i$$
这些误差最终会形成一个概率分布，假设这个未知的分布的概率密度函数为：
$$f\left(ϵ\right)$$
因为每步实验都是假设独立的，所以最终的联合概率分布可以表示为：
$$\begin{gathered} L\left(\theta \right)=f\left({ϵ}_1\right)f\left({ϵ}_2\right)\cdot \cdot \cdot f\left({ϵ}_n\right) \\ =f\left(y-y_1\right)f\left(y-y_2\right)\cdot \cdot \cdot f\left(y-y_n\right) \end{gathered}$$

这里数学王子高斯没有采用贝叶斯的推理方式，而是直接采用了最大似然估计的方法求解上面的 $L\left(\theta \right)$, 而为了配合最小二乘法的结果，去寻找一个最大似然估计值刚好是算术平均的似然函数 $f$，最终高斯证明，所有的概率密度函数中，唯一满足条件的是：
$$f(x)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{x^2}{2{\sigma }^2}}$$

(3)

上面的概率分布正是服从 $\mathcal{N}(0,{\sigma }^2)$ 正态分布的概率密度函数了！
将正态分布的概率密度函数代入 $L\left(\theta \right)$表达式可得：
$$L\left(\theta \right)=\frac{1}{(\sqrt{2\pi \sigma }{)}^n}exp\left\{-\frac{1}{2{\sigma }^2}\sum _{i=1}^n{ϵ}_i^2\right\}$$

(4)

这里想要 $L\left(\theta \right)$ 取最大值，就需要 ${\sum }_{i=1}^n{ϵ}_i^2$ 取最小值， 刚好就是最小二乘法的要求。

中心极限定理与大数定理

这里再多说几句，既然涉及到数学知识，就一并多查了一些资料，因为在整理上面内容的时候不可避免的会遇到中心极限定理和大数定理，这里简单说一下这两个定理的思想。

• 大数定理：随着样本容量 n 的增加，样本平均数将接近于总体平均数。
• 中心极限定理：随着样本容量 n 的增加，这 n 个数的均值将趋近于正态分布。

从大数定律可以知道，随着发生次数的增加，偶然最终会服从于必然（如一个猜大小的赌博游戏如果只有大，小两个选项，且发生概率各为 0.5，则长期来看这个赌博游戏会维持在输赢金额平衡，不会给赌场带来盈利也不会让赌场输钱），而中心极限定理则是可以通过部分样本来推测整体样本的分布情况（通过调查美国某地2000个人的投票意向，来预测本地对美国大选的得票数的影响）。

浅谈回归

基本概念

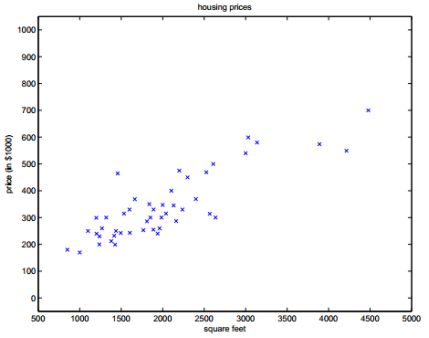
回归是指研究因变量与自变量之间确定的因果关系，建立回归模型，并根据实测数据来求解模型的各个参数，如果可以很好的拟合，则根据自变量进一步预测。

如上面的数据分布，基本可以确定横坐标的变量与纵坐标的变量是正相关的关系，可以使用：

$$y=ax+b$$
来进行拟合。 当最终确定 $a$ 和 $b$ 的值以后对于一个新的 $x$，代入方程就可以直接得到一个 $y$ 值。

线性回归

顾名思义，对于线性回归，其回归模型是一个线性表达式，直接根据下面的两张图来表示分别表示当考虑一维因素和考虑二维因素时对应的线性回归结果：
…

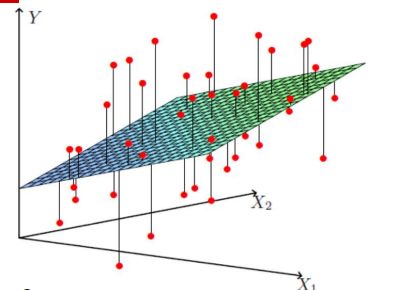
以两个自变量$x_1$，$x_2$ 为例，我们可以直接将线性回归模型的表达式表示为：
$$h_{\theta }(x)={\theta }_2{x}_2+{\theta }_1{x}_1+{\theta }_0=\sum _{i=0}^2{\theta }_i{x}_i={\theta }^{\mathbf{T}}\mathbf{x}$$

(5)

以加粗以后的字符表示 向量/矩阵。对于这个模型对于每一对$x_1$，$x_2$ ，本身就有一个真实值$y$，此外我们还可以得有一个预测值 $y={\theta }^{\mathbf{T}}\mathbf{x}$,

这里的误差:
$$ϵ=|y-y|=|y-{\theta }^{\mathbf{T}}\mathbf{x}|$$

(6)

根据中心极限定理可得 $ϵ$ 的分布是服从高斯分布的，将(6) 式代入高斯分布的概率函数中（(3) 式）最终可以得到形如（4）式的似然函数：
$$L\left(\theta \right)=\prod _{i=1}^n\frac{1}{\sqrt{2\pi \sigma }}exp\left\{-\frac{{\left(y^i-{\theta }^T{\mathbf{x}}^i\right)}^2}{2{\sigma }^2}\right\}$$

(7)

对上面的形式取 $log$：

$$\begin{gathered} l\left(\theta \right)=logL\left(\theta \right) \\ =log\prod _{i=1}^n\frac{1}{\sqrt{2\pi \sigma }}exp\left\{-\frac{{\left(y^i-{\theta }^T{\mathbf{x}}^i\right)}^2}{2{\sigma }^2}\right\} \\ =\sum _{i=1}^{n}log\frac{1}{\sqrt{2\pi \sigma }}exp\left\{-\frac{{\left(y^i-{\theta }^T{\mathbf{x}}^i\right)}^2}{2{\sigma }^2}\right\} \\ =mlog\frac{1}{\sqrt{2\pi \sigma }}-\frac{1}{{\sigma }^2}\cdot \frac{1}{2}\sum _{i=1}^n{\left(y^i-{\theta }^T{\mathbf{x}}^i\right)}^2 \end{gathered}$$

(8)

求(8)式最大就被转化为了求（9）式最小，最终由 (8) 式可以得到我们的目标函数可以简化为：
$$J\left(\theta \right)=\frac{1}{2}\sum _{i=1}^n{\left({\theta }^T{\mathbf{x}}^i-y^i\right)}^2$$

(9)

将 (9) 式都转化成矩阵表示形式：
$$J\left(\theta \right)=\frac{1}{2}{\left(X\theta -\mathbf{y}\right)}^T\left(X\theta -\mathbf{y}\right)$$

(10)

最小二乘法意义下的解析解

这里首先得知道线性代数中关于矩阵求导的几个公式：
$$\begin{gathered} \frac{\partial {\theta }^{T}A}{\partial \theta }=A \\ \frac{\partial A\theta }{\partial \theta }=A^T \\ \frac{\partial {\theta }^{T}A\theta }{\partial \theta }=2A\theta \end{gathered}$$

(11)

由公式（11）可以推导出 $J(\theta )$ 对于 $\theta$ 的偏导为：
$$\begin{gathered} J(\theta )=\frac{1}{2}\left({\theta }^T{X}^{T}X\theta -{\theta }^T{X}^T\mathbf{y}-{\mathbf{y}}^{T}X\theta +{\mathbf{y}}^T\mathbf{y}\right) \\ \frac{\partial J(\theta )}{\partial \theta }=\frac{1}{2}\left(2X^{T}X\theta -X^T\mathbf{y}-{\left({\mathbf{y}}^{T}X\right)}^T\right),又因为{\left({\mathbf{y}}^{T}X\right)}^T=X^T\mathbf{y} \end{gathered}$$
$$\frac{\partial J(\theta )}{\partial \theta }=\frac{1}{2}\left(2X^{T}X\theta -2X^T\mathbf{y}\right)=X^{T}X\theta -X^T\mathbf{y}$$

(12)

另式(12) 为 0，最终求得 $\theta$ 的解析解为：
$$\theta =(X^{T}X{)}^{-1}{X}^T\mathbf{y}$$

(13)

为了保证 $(X^{T}X{)}^{-1}$ 正定成立或者防止过拟合，增加了一个 $\lambda$ 扰动：
$$\theta =(X^{T}X+\lambda I{)}^{-1}{X}^T\mathbf{y}$$

(14)

其实这里的 $\lambda$ 扰动对应的就是 L-norm 正则化项，这里顺便引出下面的不同回归形式。

LASSO 回归，岭回归

它们的区别只是最后加入的正则项不一样。

• LASSO 回归（L1-norm）：
  $$J\left(\theta \right)=\frac{1}{2}\sum _{i=1}^n{\left({\theta }^T{\mathbf{x}}^i-y^i\right)}^2+\lambda \sum _{j=1}^n|{\theta }_j|$$
• 岭回归 (L2-norm):
  $$J\left(\theta \right)=\frac{1}{2}\sum _{i=1}^n{\left({\theta }^T{\mathbf{x}}^i-y^i\right)}^2+\lambda \sum _{j=1}^n{\theta }_j^2$$

当我们知道了 X矩阵，知道了y矩阵，可以通过解析解直接求出 $\theta$ 值，但是在实际算法实现过程中，我们很少直接那么做，因为遇到的机器学习问题中可能会遇到特征或者样本数量维度很大的情况（百万级别），这个时候直接求解析解就显得不那么现实了。

梯度下降算法

对于梯度下降算法的原理不再赘述了，相信大家都有所了解，我们需要沿着$J(\theta )$的负梯度的方向，更新 $\theta$使之最小。
$$\theta =\theta -\alpha \frac{\partial J(\theta )}{\partial \theta }$$

(15)

$\alpha$ 为学习率，其中：
$$\begin{gathered} \frac{\partial J(\theta )}{\partial {\theta }_i}=\frac{\partial }{\partial \theta }\frac{1}{2}(h_{\theta }(x)-y{)}^2 \\ =(h_{\theta }(x)-y)\frac{\partial }{\partial {\theta }_i}\left(\sum _{i=1}^n{\theta }_i{x}_i-y\right)=(h_{\theta }(x)-y)x_i \end{gathered}$$

(16)

所以最后的表现形式为：
$${\theta }_j:={\theta }_j-\alpha \sum _{i=1}^m\left(h_{\theta }\left(x^i\right)-y^i\right)x_j^i$$

(17)

最后根据公式（17）一步步收敛到全局最优，这里的 $m$ 代表样本数，通常就是我们训练时设置的的 batch size。

Logistic 回归

用回归做分类问题就不能直接用线性回归了，这节要谈到的 Logistic回归才是回归做分类（二分类）的首选工具，多类别分类的 Logistic回归也称做 Softmax 回归。这里我们以经典的二分类为例进行说明。
线性回归的回归模型可以简单的表示为：$$h_{\theta }(x)={\theta }^{\mathbf{T}}\mathbf{x}$$
这里 Logistic 回归则是用到了 Logistic/ sigmoid 函数来表达回归模型：
$$h_{\theta }(x)=g({\theta }^{\mathbf{T}}\mathbf{x})=\frac{1}{1+\mathbf{e}\mathbf{x}\mathbf{p}\left\{-{\theta }^{\mathbf{T}}\mathbf{x}\right\}}$$

(18)

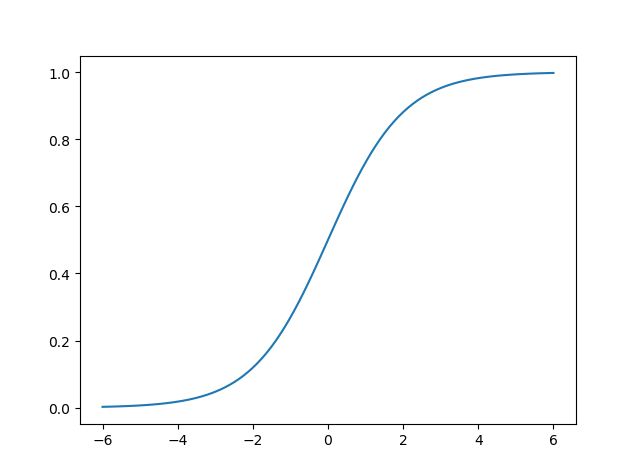
Logistic/ sigmoid 函数 $g\left(x\right)$ 的函数曲线如下图所示，可以看到最后的数值的范围是[0,1]之间。

且经过计算可以得到 Logistic/ sigmoid 函数的导数可以直接表达为：

$$g^{\prime }\left(x\right)=g\left(x\right)\left(1-g\left(x\right)\right)$$

参数估计

由上面的 logistic 最后取值范围是 [0,1] 之间的性质，我们可以直接将 $h_{\theta }(x)$ 看作是一个类别的概率，二分类问题中，另一个问题的概率就是 $1-h_{\theta }(x)$，用数学语言表示即：
$$P(y|x;\theta )=\{\begin{array}{c}{h}_{\theta }(x),y=1\\ 1-h_{\theta }(x),y=0\end{array}$$
将上式等效转化为：
$$P(y|x;\theta )={\left(h_{\theta }(x)\right)}^y{\left(1-h_{\theta }(x)\right)}^{1-y}$$

(19)

由上面的概率公式可以得到 Logistic 回归的似然函数：
$$L\left(\theta \right)=\prod _{i=1}^{m}P(y^i|x^i;\theta )$$ $$=\prod _{i=1}^m{\left(h_{\theta }(x^i)\right)}^{y^i}{\left(1-h_{\theta }(x^i)\right)}^{1-y^i}$$

(20)

对上面的式子取对数可以得到：
$$\begin{gathered} l\left(\theta \right)=logL\left(\theta \right) \\ =\sum _{i=1}^m{y}^{i}log\left(h_{\theta }(x^i)\right)+1-y^{i}log\left(1-h_{\theta }(x^i)\right) \end{gathered}$$

(21)

对式（21）求导可以得到：

$\frac{\partial }{\partial {\theta }_j}l\left(\theta \right)=\left(y\frac{1}{g\left({\theta }^{T}X\right)}-\left(1-y\right)\frac{1}{1-g\left({\theta }^{T}X\right)}\right)\frac{\partial }{\partial {\theta }_j}g\left({\theta }^{T}X\right)$

$=\left(y\frac{1}{g\left({\theta }^{T}X\right)}-\left(1-y\right)\frac{1}{1-g\left({\theta }^{T}X\right)}\right)g\left({\theta }^{T}X\right)\left(1-g\left({\theta }^{T}X\right)\right)\frac{\partial }{\partial {\theta }_j}{\theta }^{T}X$

$=\left(y\left(1-g\left({\theta }^{T}X\right)\right)-\left(1-y\right)g\left({\theta }^{T}X\right)\right)x_j=\left(y-h_{\theta }\left(x\right)\right)x_j$

最后同样使用梯度下降算法对 Logistic 模型进行迭代巡练：
$${\theta }_j:={\theta }_j-\alpha \sum _{i=1}^m\left(h_{\theta }\left(x^i\right)-y^i\right)x_j^i$$

（注：这里 Logistic 回归没有解析解，所以只能用梯度算法求解）

与线性回归的关系

上面的分析可以看到线性回归与 Logistic 回归有相同的梯度更新形式。因为 Logistic 回归是对数线性模型。
一个事件的几率（odd）指该事件发生的概率与该事件不发生的概率的比值，对数几率就是对几率的表达式取对数，即：
$$logit(p)=log\frac{p}{1-p}=log\frac{h_{\theta }\left(x\right)}{1-h_{\theta }\left(x\right)}=log\left(\frac{\frac{1}{1+e^{-{\theta }^{T}X}}}{\frac{e^{-{\theta }^{T}X}}{1-e^{-{\theta }^{T}X}}}\right)={\theta }^{T}X$$

主要参考文献：
如何理解最小二乘法？
正态分布的前世今生 (上)
https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-vector_identities