本节主要通过几个例子来介绍贪心策略,主要包括背包问题、哈夫曼编码和最小生成树
贪心算法顾名思义就是每次都贪心地选择当前最好的那个(局部最优解),不去考虑以后的情况,而且选择了就不能够“反悔”了,如果原问题满足贪心选择性质和最优子结构,那么最后得到的解就是最优解。贪心算法和其他的算法比较有明显的区别,动态规划每次都是综合所有子问题的解得到当前的最优解(全局最优解),而不是贪心地选择;回溯法是尝试选择一条路,如果选择错了的话可以“反悔”,也就是回过头来重新选择其他的试试。
这个算法想必大家也都很熟悉了,我觉得贪心法总是比较容易想到,但是很难证明它是正确的,所有对于一类问题,条件稍有不同也许就不能使用贪心策略了。这一节采用类似上节的形式,记录下原书中的一些重点难点内容
[果然贪心我领悟的不够,很多问题我貌似都讲不到点子上,大家将就着看下]
1.匹配问题 matching problem (maximum-weight matching problem)
问题是这样的,有一群人打算一起跳探戈,跳之前要进行分组,一个男人和一个女人成为一组,而且任意一个异性组合都会一个相应的匹配值(compatibility),目标是求使得匹配值之和达到最大的分组方式。
To be on the safe side, just let me emphasize that this greedy solution would not work in general, with an arbitrary set of weights. The distinct powers of two are key here.
一般情况下,如果匹配值是任意值的话,这个问题使用贪心法是不行的!但是如果匹配值都是2的整数幂的话,那么贪心法就能解决这个问题了![这点我不明白,这是此题的一个重点,避免误导,我附上原文,不解释了,如果读者有明白了的希望能留言告知,嘿嘿]
In this case (or the bipartite case, for that matter), greed won’t work in general. However, by some freak coincidence, all the compatibility numbers happen to be distinct powers of two. Now, what happens?
Let’s first consider what a greedy algorithm would look like here and then see why it yields an optimal result. We’ll be building a solution piece by piece—let the pieces be pairs and a partial solution be a set of pairs. Such a partial solution is valid only if no person in it participates in two (or more) of its pairs. The algorithm will then be roughly as follows:
- List potential pairs, sorted by decreasing compatibility.
- Pick the first unused pair from the list.
- Is anyone in the pair already occupied? If so, discard it; otherwise, use it.
- Are there any more pairs on the list? If so, go to 2.
As you’ll see later, this is rather similar to Kruskal’s algorithm for minimum spanning trees (although that works regardless of the edge weights). It also is a rather prototypical greedy algorithm. Its correctness is another matter. Using distinct powers of two is sort of cheating, because it would make virtually any greedy algorithm work; that is, you’d get an optimal result as long as you could get a valid solution at all. Even though it’s cheating (see Exercise 7-3), it illustrates the central idea here: making the greedy choice is safe. Using the most compatible of the remaining couples will always be at least as good as any other choice.
贪心解决的思路大致如下:首先列举出所有可能的组合,然后将它们按照匹配值进行降序排序,接着按顺序从中选择前面没有使用过而且人物没有在前面出现过的组合,遍历完整个序列就得到了匹配值之和最大的分组方式。
[原书关于稳定婚姻的扩展知识 EAGER SUITORS AND STABLE MARRIAGES]
There is, in fact, one classical matching problem that can be solved (sort of) greedily: the stable marriage problem. The idea is that each person in a group has preferences about whom he or she would like to marry. We’d like to see everyone married, and we’d like the marriages to be stable, meaning that there is no man who prefers a woman outside his marriage who also prefers him. (To keep things simple, we disregard same-sex marriages and polygamy here.)
There’s a simple algorithm for solving this problem, designed by David Gale and Lloyd Shapley. The formulation is quite gender-conservative but will certainly also work if the gender roles are reversed. The algorithm runs for a number of rounds, until there are no unengaged men left. Each round consists of two steps:
- Each unengaged man proposes to his favorite of the women he has not yet asked.
- Each woman is (provisionally) engaged to her favorite suitor and rejects the rest.
This can be viewed as greedy in that we consider only the available favorites (both of the men and women) right now. You might object that it’s only sort of greedy in that we don’t lock in and go straight for marriage; the women are allowed to break their engagement if a more interesting suitor comes along. Even so, once a man has been rejected, he has been rejected for good, which means that we’re guaranteed progress.
To show that this is an optimal and correct algorithm, we need to know that everyone gets married and that the marriages are stable. Once a woman is engaged, she stays engaged (although she may replace her fiancé). There is no way we can get stuck with an unmarried pair, because at some point the man would have proposed to the woman, and she would have (provisionally) accepted his proposal.
How do we know the marriages are stable? Let’s say Scarlett and Stuart are both married but not to each other. Is it possible they secretly prefer each other to their current spouses? No: if so, Stuart would already have proposed to her. If she accepted that proposal, she must later have found someone she liked better; if she rejected it, she would already have a preferable mate.
Although this problem may seem silly and trivial, it is not. For example, it is used for admission to some colleges and to allocate medical students to hospital jobs. There have, in fact, been written entire books (such as those by Donald Knuth and by Dan Gusfield and Robert W. Irwing) devoted to the problem and its variations.
2.背包问题
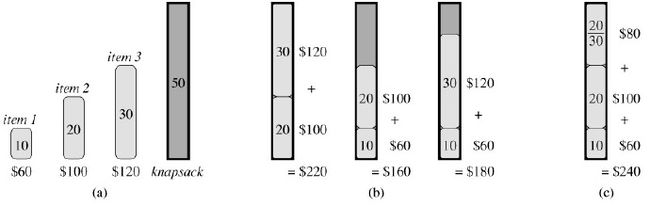
这个问题大家很熟悉了,而且该问题的变种很多,常见的有整数背包和部分背包问题。问题大致是这样的,假设现在我们要装一些物品到一个书包里,每样物品都有一定的重量w和价值v,但是呢,这个书包承重量有限,所以我们要进行决策,如何选择物品才能使得最终的价值最大呢?整数背包是说一个物品要么拿要么不拿,比如茶杯或者台灯等等,而部分背包问题是说一个物品你可以拿其中的一部分,比如一袋子苹果放不下可以只装半袋子苹果。[更加复杂的版本是说每个物品都有一定的体积,同时书包还有体积的限制等等]
很显然,部分背包问题是可以用贪心法来求解的,我们计算每个物品的单位重量的价值,然后将它们降序排序,接着开始拿物品,只要装得下全部的该类物品那么就全装进去,如果不能全部装下就装部分进去直到书包载重量满了为止,这种策略肯定是正确的。
但是,整数背包问题就不能用贪心策略了。整数背包问题还可以分成两种:一种是每类物品数量都是有限的(bounded),比如只有3个茶杯和2个台灯;还有一种是数量无限的(unbounded),也就是你想要多少有多少,这两种都不能使用贪心策略。0-1背包问题是典型的第一种整数背包问题,看下算法导论上的这个例子就明白了,在(b)中,虽然物品1单位重量的价值最大,但是任何包含物品1的选择都没有超过选择物品2和物品3得到的最优解220;而(c)中能达到最大的价值是240。
整数背包问题还没有能够在多项式时间内解决它的算法,下一节我们介绍的动态规划能够解决0-1背包问题,但是是一个伪多项式时间复杂度。[实际时间复杂度是O(nw),n是物品数目,w是书包载重量,严格意义上说这不是一个多项式时间复杂度]
There are two important cases of the integer knapsack problem—the bounded and unbounded cases. The bounded case assumes we have a fixed number of objects in each category,4 and the unbounded case lets us use as many as we want. Sadly, greed won’t work in either case. In fact, these are both unsolved problems, in the sense that no polynomial algorithms are known to solve them. There is hope, however. As you’ll see in the next chapter, we can use dynamic programming to solve the problems in pseudopolynomial time, which may be good enough in many important cases. Also, for the unbounded case, it turns out that the greedy approach ain’t half bad! Or, rather, it’s at least half good, meaning that we’ll never get less than half the optimum value. And with a slight modification, you can get as good results for the bounded version, too. This concept of greedy approximation is discussed in more detail in Chapter 11.
3.哈夫曼编码
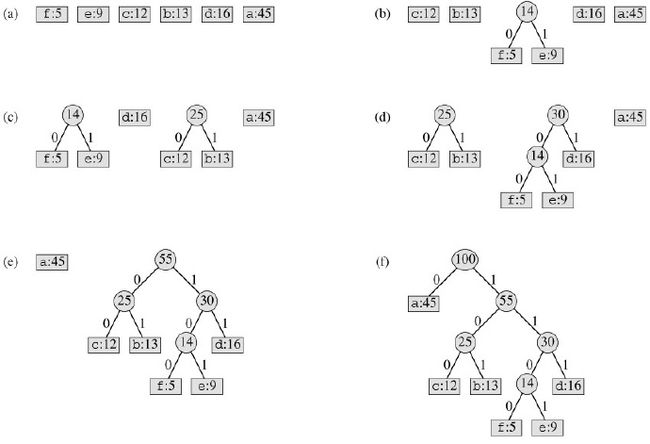
这个问题原始是用来实现一个可变长度的编码问题,但可以总结成这样一个问题,假设我们有很多的叶子节点,每个节点都有一个权值w(可以是任何有意义的数值,比如它出现的概率),我们要用这些叶子节点构造一棵树,那么每个叶子节点就有一个深度d,我们的目标是使得所有叶子节点的权值与深度的乘积之和Σwidi最小。
很自然的一个想法就是,对于权值大的叶子节点我们让它的深度小些(更加靠近根节点),权值小的让它的深度相对大些,这样的话我们自然就会想着每次取当前权值最小的两个节点将它们组合出一个父节点,一直这样组合下去直到只有一个节点即根节点为止。如下图所示的示例
代码实现比较简单,使用了heapq模块,树结构是用list来保存的,有意思的是其中zip函数的使用,其中统计函数count作为zip函数的参数,详情见python docs