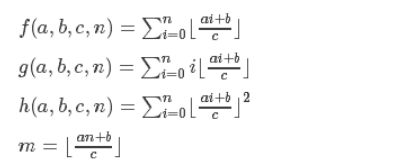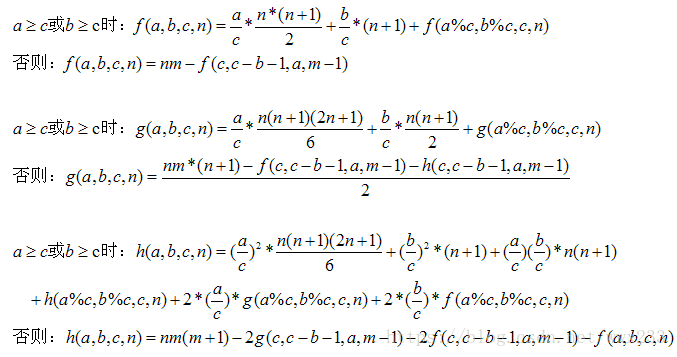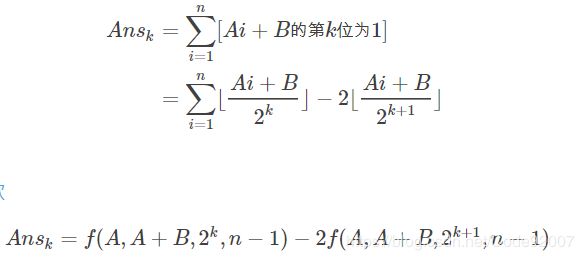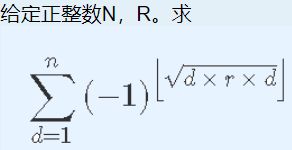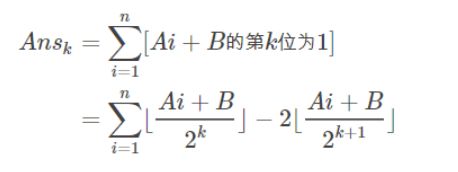(转载)类欧几里得(知识点整理+板子总结)

思路来源

https://blog.csdn.net/wwx233/article/details/82431820

https://www.cnblogs.com/cyz666/p/7083213.html

https://blog.csdn.net/qq_35649707/article/details/79169099(证明清楚详细)

https://blog.csdn.net/white_elephant/article/details/79047813

心得

一直自己想学，camp回来不会，终于在归神的督促(ruanmoyingpao)下，学会了

知识点整理

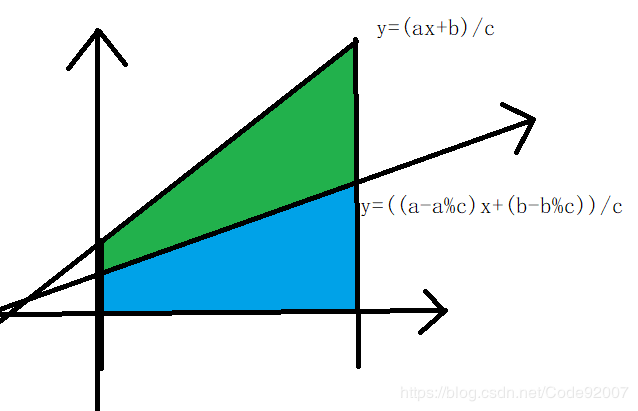
类欧可以等价于求y=(ax+b)/c这条直线与x=0和x=n y=0围成的直角梯形上的整点的个数，

在直线上的统计在内，在x=0和x=n上的统计在内，在y=0上的不统计

几个常用不等式，在下式推导中起作用，主要变竖向枚举为横向枚举，

i和j互换的时候，交换枚举顺序，相当于把起初求每个竖条上的值的过程，变成求每个横条的过程

观察n a b c的位置，令m=(an+b)/c，所以就可以从f(a,b,c,n)递归到f(c,c-b-1,a,m-1)

 

直接记公式就好，a>=c或b>=c时，

其等价意义，相当于在y=(ax+b)/c下画了一条y=((a-a%c)x+(b-b%c))/c的直线，将梯形分成两个部分

而新直线是整除c的，所以蓝色内面积可以直接统计整点个数，

上面的三角形内整点个数利用坐标变换再求，斜率和截距就降到

一般常用的类欧，f、g、h

对于n1e9级别的询问，f是O(logn)的，g和h大概在1e7水准

f模板(前者利用ull自然取模)

#include
#include
#define ll unsigned long long

using namespace std;

ll f(ll a,ll b,ll c,ll n){
    if(a==0){
        return (n+1)*(b/c);
    }
    if(a

LL S(LL k)
{   
    return (k*(k+1)/2ll)%MOD;
}
LL f(LL a,LL b,LL c,LL n)
{
    if(!a)return 0;
    if(a>=c || b>=c)
      return ((a/c)*S(n)%MOD+(n+1)*(b/c)%MOD+f(a%c,b%c,c,n))%MOD;
    LL m=(a*n+b)/c;
    return (m*n%MOD-f(c,c-b-1,a,m-1)+MOD)%MOD;
}

g的模板

#include 
#include 
#include 
#include 

using namespace std;

const int mo=1e9+7,inv2=500000004,inv6=166666668;

typedef long long LL;

int a,b,c,l,r;

struct data
{
    int f,g,h;
};

data calc(int a,int b,int c,LL n)
{
    data tmp;
    if (!a)
    {
        tmp.f=tmp.g=tmp.h=0;
        return tmp;
    }
    if (a>=c || b>=c)
    {
        tmp=calc(a%c,b%c,c,n);
        n%=mo;
        tmp.h=(tmp.h+
                n*(n+1)%mo*(2*n+1)%mo*inv6%mo*(a/c)%mo*(a/c)%mo
                  +(n+1)*(b/c)%mo*(b/c)%mo
                    +(LL)2*(a/c)*tmp.g%mo
                      +(LL)2*(b/c)*tmp.f%mo
                        +n*(n+1)%mo*(a/c)%mo*(b/c))%mo;
        tmp.f=(tmp.f
                +n*(n+1)/2%mo*(a/c)
                    +(n+1)*(b/c))%mo;
        tmp.g=(tmp.g
                +n*(n+1)%mo*(2*n+1)%mo*inv6%mo*(a/c)
                    +n*(n+1)/2%mo*(b/c))%mo;
        return tmp;
    }
    LL m=((LL)a*n+b)/c;
    data nxt=calc(c,c-b-1,a,m-1);
    n%=mo; m%=mo;
    tmp.f=((n*m-nxt.f)%mo+mo)%mo;
    tmp.g=(LL)((n*(n+1)%mo*m-nxt.f-nxt.h)%mo+mo)*inv2%mo;
    tmp.h=((m*(m+1)%mo*n-(LL)2*(nxt.g+nxt.f)%mo-tmp.f)%mo+mo)%mo;
    return tmp;
}

int main()
{
    freopen("task.in","r",stdin); freopen("task.out","w",stdout);
    scanf("%d%d%d%d%d",&a,&c,&b,&l,&r);
    printf("%d\n",(calc(a,b,c,r).g-calc(a,b,c,l-1).g+mo)%mo);
    return 0;
}

例题

JZOJ3492 数数(count)

我们知道，一个等差数列可以用三个数A,B,N表示成如下形式： 
B+A,B+2A,B+3A⋯B+NA
ztxz16想知道对于一个给定的等差数列，把其中每一项用二进制表示后，一共有多少位是1
A<=1e4，B<=1e16，N<=1e12

 

有个很经典的类欧套路，k从0开始

二进制下，第k位是否为1，等于(原数>>k)-2*(原数>>(k+1))，

前者取到了自第k位起的高位，后者高位对齐减掉了(k+1)位以上的高位

可以把i从1到n变成i从0到n-1，也就是提一个A出来，再做，于是就是类欧板子题

#include
#include
#define ll unsigned long long

using namespace std;

ll f(ll a,ll b,ll c,ll n){
    if(a==0){
        return (n+1)*(b/c);
    }
    if(a

【GDOI2018模拟8.8】超级绵羊异或

求(a) xor (a + b) xor (a + b * 2) xor … xor (a + b * (n - 1))。

对于100%的数据，t<=1e4，a, n<=1e9， b<=1e9；

 

写成求和形式，考虑最后第k位的奇偶，即像上题一样，判断每一位的出现次数，再类欧

#include
#include
#define ll unsigned long long

using namespace std;

ll f(ll a,ll b,ll c,ll n){
    if(a==0){
        return (n+1)*(b/c);
    }
    if(a

BZOJ3817

对于 100% 的数据，满足 n≤10^9,r≤10^4,T≤10^4。

考虑幂的奇偶会对答案造成不同贡献，本质上是幂的第1位是否为1

仍利用本式求Ans0，注意[bool]取值只有0和1，但本题中若为0则应+1，若为1则应-1

所以对布尔式的贡献线性变换一下，搞成1-2*Ans0

后续，由于sqrt(r)是实数，实数类欧不会搞，

不想学了，留坑，无限期待填