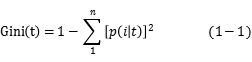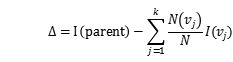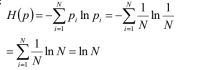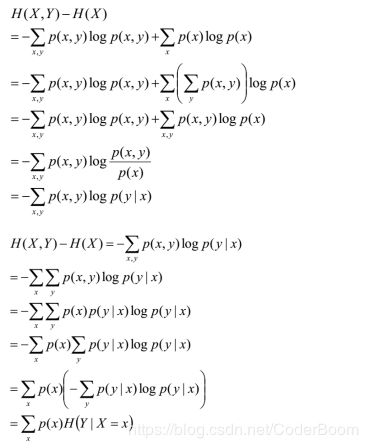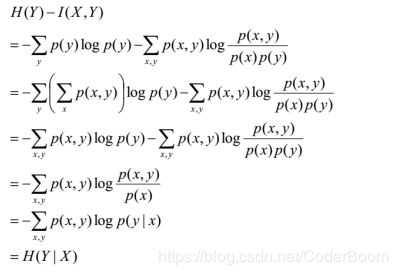推荐系统-用户标签预测算法基础实践-决策树(一)
推荐系统-用户标签预测算法基础实践
1.用户画像概述
- 用户画像就是给到用户打标签
- 用户画像
- 用户角色
- 用户属性
- 用户画像和用户角色较为接近,而用户属性使用户的画像中的子集
- 用户画像阶段
- 1.用户画像基础
- 2.用户画像指标体系
- 3.标签数据存储方式
- 4.标签数据开发
- 5.性能优化及作业调度
- 6.用户画像应用及优化
- 用户画像基础场景用
- 搜索领域
- 个性化推荐领域
- 其他领域
- 个人征信数据数据特征
- 身份属性
- 履约能力
- 信用记录
- 社交资料
- 公共记录信息
- 网站流量指标分析
- 网站流量统计指标包括
- 独立访问者数量(UV)
- 重复访问者数量(RV)
- 页面浏览数(PV)
- 每个访问者的页面浏览数(Page Views per user)
- 某些具体文件/页面的统计指标 , 如页面显示次数 , 文件下载次数等
- 用户行为指标
- 用户在网站停留时间
- 用户来源
- 用户所使用的搜索引擎及其关键词
- 在不同时段的用户访问量情况等
- 用户浏览网站的方式
- 时间 , 设备 , 浏览器名称和版本 , 操作系统等
- 用户浏览网站的方式相关统计指标主要包括
- 用户上网设备类型
- 用户浏览器的名称和版本
- 访问者电脑分辨率显示模式
- 用户所使用的操作系统名称和版本
- 用户所在地理区域分布状况等
- 提高网站流量的方法
- 通过互刷软件
- 通过广告联盟
- 通过友情链接
- 网站流量统计指标包括
2.常见用户画像业务分析指标
- 以电商为例展开
- 电商总总体运营指标
- 流量类指标
- 独立访客数(UV)
- 页面访问数(PV)
- 人均页面访问数
- 订单产生效率指标
- 总订单数量
- 访问到下单转化率
- 总体销售业绩指标
- 成交金额(GMV)
- 销售金额
- 客单价
- 整体指标
- 销售毛利
- 毛利率
- 流量类指标
- 网站流量指标
- 流量规模类指标
- 独立访客数(UV)
- 页面访问数(PV)
- 流量成本类指标
- 访客获取成本
- 流量质量类指标
- 跳出率 : 为浏览单页即退出的次数/该页访问次数,跳出率只能衡量该页做为着陆页面(LandingPage)的访问。
- 页面访问时长
- 人均页面访问数
- 会员类指标
- 注册会员数
- 活跃会员数
- 活跃会员率
- 会员复购率
- 会员平均购买次数
- 会员回购率
- 会员留存率 : 留存率反应的是电商留住会员的能力。
- 流量规模类指标
- 网站销售指标
- 购物车类指标
- 基础类统计
- 加入购物车次数
- 加入购物车买家数
- 加入购物车买家数
- 加入购物车商品数
- 转化类统计
- 购物车支付转化率
- 基础类统计
- 下单类指标
- 基础类统计
- 下单笔数
- 下单金额
- 下单买家数
- 转化类统计
- 浏览下单转化率
- 基础类统计
- 支付类指标
- 基础类统计
- 支付金额
- 支付买家数
- 支付商品数
- 转化类统计
- 浏览-支付买家转化率
- 下单-支付金额转化率
- 下单-支付买家数转化率
- 下单-支付时长
- 基础类统计
- 交易类指标
- 成功类统计
- 交易成功订单数
- 交易成功金额
- 交易成功买家数
- 交易成功商品数
- 失败类统计
- 交易失败订单数
- 交易失败订单金额
- 交易失败订单买家数
- 交易失败商品数
- 退款类统计
- 退款总订单量
- 退款金额
- 退款率
- 成功类统计
- 购物车类指标
- 客户价值类指标
- 客户指标
- 累计购买客户数
- 客单价
- 新客户指标
- 新客户数量
- 新客户获取成本
- 新客户客单价
- 老客户指标
- 消费频率
- 最近一次购买时间
- 消费金额
- 重复购买率
- 客户指标
- 商品类指标
- 产品总数指标
- SKU数 : SKU是物理上不可分割的最小存货单位。
- SPU数 : 属性值、特性相同的商品就可以称为一个SPU。
- 在线SPU数 : 在线商品的SPU数
- iphone5S是一个SPU,而iPhone 5S配置为16G版、4G手机、颜色为金色、网络类型为TD-LTE/TD-SCDMA/WCDMA/GSM则是一个SKU。
- 产品优势性指标
- 独家产品收入比重 : 独家销售的产品收入占总销售收入的比例
- 品牌存量
- 品牌数
- 在线品牌数
- 上架
- 上架商品SKU数
- 上架商品SPU数
- 上架在线SPU数
- 上架商品数
- 上架在线商品数
- 首发
- 首次上架商品数
- 首次上架在线商品数
- 产品总数指标
- 市场竞争类的指标
- 市场营销活动指标
- 新增访问人数
- 新增注册人数
- 总访问次数
- 订单数量
- 下单转化率
- ROI : 投资回报率(ROI)是指,某一活动期间,产生的交易金额与活动投放成本金额的比值。
- 广告投放指标
- 新增访问人数
- 新增注册人数
- 总访问次数
- 订单数量
- UV订单转化率
- 广告投资回报率
- 风控类指标
- 买家评价指标
- 买家评价数
- 买家评价卖家数
- 买家评价上传图片数
- 买家评价率
- 买家好评率
- 买家差评率
- 投诉指标
- 发起投诉(申诉)数
- 投诉率
- 撤销投诉(申诉)数
- 买家评价指标
- 市场竞争类指标
- 市场份额相关
- 市场占有率
- 市场扩大率
- 用户份额
- 网站排名
- 交易额排名
- 流量排名
- 市场份额相关
- 市场营销活动指标
- 电商总总体运营指标
3.如何利用用户行为数据
-
用户的静态数据–mysql
-
用户的动态数据–浏览、加购、收藏等
-
标签形态及标签建模
- 标签 : 表征了内容,用户对该内容有兴趣、偏好、需求等等。
- 权重 : 表征了指数,用户的兴趣、偏好指数,也可能表征用户的需求度,可以简单的理解为可信度,概率。
- 权重—时间衰减因子,地点因子,是购购买
- 数据建模方法: 标签=用户标识 + 时间 + 行为类型 + 接触点(网址+内容)的聚合
-
算法路线及算法思路:
- 用户画像+推荐系统===利用机器学习
-
标签层级
- 用户+商品+环境
-
属性的显隐性反馈
4.如何利用用户标签数据
- 当有了标签之后如何使用?
- 在页面中设置依稀标签选项
- 如何推荐标签?
- 基于物品的热门商品推荐
- 基于当前浏览物品的热门商品推荐
- 基于内容的相似度推荐(经常使用标签)
5.用户画像建模分类
- 如何对用户画像建模?
- 定性
- 定量建立模型
- 用户画像打的哪几类标签:?
- 统计类标签-pv
- 规则类标签-近30天活跃度(规则)
- 挖掘类(机器学习算法构建)
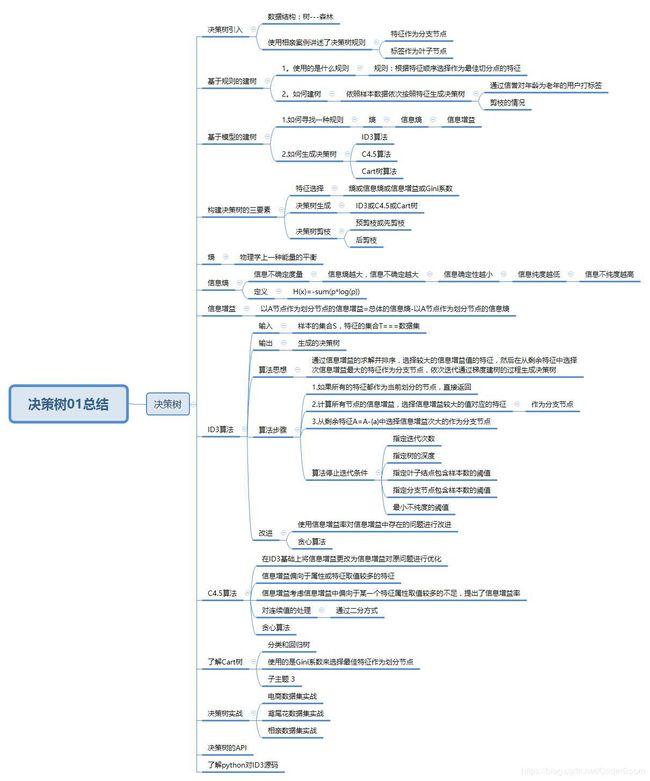
6.决策树引入
- 决策树----类似树的概念
- 树—现实生活中树结构–树根–树干—树枝—树叶
- 数据结构中树:根节点—分支节点-----叶子结点
- 机器学习中的树:分支节点----叶子节点
- 分支节点:由特征充当
- 叶子节点:由类别标签列的取值充当
7.电商实例引入详解
- 通过对数据集的简单描述强化数据集的构成
- 基于规则建树
- 规则建立
- 选择特征充当分支节点 , 类别标签充当叶子节点
- 依照特征或属性出现的顺序指定规则 , 建立决策树
- 首先选择年龄、收入、学生、信誉依次构建决策树
- 根据决策树可以对部分节点进行剪枝,使得决策树变得更加简单
- 根据决策树回答业务决策问题
- 根据已有的特征对决策树进行分类
- 如果中年人直接推荐商品(给业务人员决策)
- 优化 : 基于模型的建树
8.构建决策树三要素
- 特征选择:选择有较强分类能力的特征 . 如何选择特征?依靠信息熵、信息增益、 信息增益率等进行特征选择
- 决策树生成:决策树生成依赖于特征选择,ID3采用信息增益作为特征选择度量,信息增益率作为C4.5算法的特征选择,Gini系数组成Cart树算法
- 决策树剪枝:先剪枝(树生成之前或过程中进行剪枝)和后剪枝(树生长完成之后进行剪枝)
9.熵和信息熵详解
- 熵:物理学上,用于能量的分布的均匀性
- 信息熵:信息论上,用于消除信息的不确定性
- 信息熵:首先定义一个不确定性函数
I(x)=plog(1/p),对不确定性函数求解期望,期望就是E(x)=-sum(xlog(x)) - 信息熵越大,信息的不确定性越大,信息的确定性越小,信息的纯度越低
- 信息熵越小,信息的不确定性越小,信息的确定性越大,信息的纯度越高
- 如果用于决策树的分支,优先选择信息熵小的值作为分支节点,构建决策树。
- 概念学习系统使用信息熵
10.信息增益与ID3算法详解
- 信息增益:信息获取量 === >
Gain(A) = Info(D)-Info_A(D) - 以A节点作为分支节点的信息增益=总体的信息熵-以A节点作为分支节点的信息熵
- 总体信息熵是求类别标签的信息熵 , 特征的信息熵是在类别标签条件下的信息熵
- 信息增益越大,信息熵越小,信息的不确定性越小,信息的确定性越大,信息的纯度越高
- 信息增益越小,信息熵越大,信息的不确定性越大,信息的确定性越小,信息的纯度越低
- 优先选择信息增益较大的特征作为分支节点
- ID3算法:属于决策树的生成算法
- 输入:样本的集合,属性的集合
- 输出:ID3决策树
- 算法步骤:
- 1.如果所有的属性都处理完毕,直接返回,否则继续下一步
- 2.计算所有的特征的信息增益,选择信息增益较大的值对应的特征作为分支节点
- 3.从剩余的属性中选择次信息增益较大的值对应的特征继续分类,直到满足停止条件,递归构建决策树
- 算法停止迭代的条件:
- 如果样本均分类,就停止迭代
- 如果没有属性被用于进一步划分,停止迭代
- 如果达到指定的迭代次数,停止迭代
- 如果达到设定的树的深度,停止迭代
- 如果叶子节点包含的样本个数达到指定阈值,也停止迭代
- 如果分支节点包含的样本个数达到指定的阈值,也停止迭代
- 如果最大不纯度下降小于a的时候,停止迭代
- 电商购买数据集案例:
- Gain(age)=info(D)-info(age)
11.决策树其他优化算法
- C4.5算法—使用信息增益率—在信息的增益基础上增加了信息熵作为分母进行对比
- 信息增益率 : Gainr(A) = Gain(A)/H(A) (H(A)即A的信息熵)
- Cart树算法—分类和回归算法-----利用Gini系数
- 所有的决策树都是贪心算法 , 自上而下 ; 区别 : 属性选择度量方法不同
-
贪心算法:顾名思义,贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑,它所作出的选择只是在某种意义上的局部最优选择。
无论哪种方法构建树,因为树的构建过程是递归形式的,所以有可能出现树的过拟合情况
12.树剪枝详解
-
先剪枝(较多)
- 在树的生长过程中进行剪枝
- 如果没有属性被用于进一步划分,停止迭代
- 如果达到指定的迭代次数,停止迭代
- 如果达到设定的树的深度,停止迭代
- 如果叶子节点包含的样本个数达到指定阈值,也停止迭代
- 如果分支节点包含的样本个数达到指定的阈值,也停止迭代
- 如果最大不纯度下降小于a的时候,停止迭代
- 在树的生长过程中进行剪枝
-
后剪枝
- 在决策树生长完成后进行剪枝
- 利用MEP最小错误率剪枝技术进行剪枝
- 利用叶子结点替换子树
- 利用分支中常出现的子树替换原子树
-
剪枝系数(了解)
- 定义决策树的损失函数
- C(X)=SUM(Ni*H(x))
- Ni叶子节点的个数 , H(x)叶子节点的熵
- alpha为剪枝系数,剪枝系数越小越好,选择不同的alpha
- 定义决策树的损失函数
-
剪枝算法
-
决策树算法的优点
- 直观,便于理解,小规模数据集有效
- 执行效率高,执行只需要一次构建,可反复使用
-
决策树算法的缺点
- 处理连续变量不好,较难预测连续字段
- 类别较多时,错误增加的比较快
- 对于时间序列数据需要做很多的预处理
- 规模性一般
- 实际分类的时候只能根据一个字段进行
-
决策树算法处理连续值
- 连续值的处理:由于连续属性的可取值数目不在有限,因此,不能直接根据连续属性的取值对结点进行划分。此时,我们采用连续值离散化的技术,最简单的是采用二分法(将样本的属性取值从大到小排序,找一个划分点将样本集分成两个子集,大于划分点的集合是决策树的一个分支,小于划分点的是决策树的一个分支)对连续属性进行处理,这也是C4.5算法采用的策略。
13.电商案例ID3算法实例详解
- 电商数据集1024样本,每个特征具体取值的概率清楚
- 求解特征的信息增益=总体信息熵-以划分节点作为分支节点的信息熵
- 求解最大的信息增益值,作为分支节点,依次选择最大的信息增益值
- 比之前绘制的基于规则建树,简化了许多
- 决策树算法能够选择最重要的特征---------信息增益
ID3步骤图解如下
总结 : 根据信息熵和信息增益得到的决策树和之前利用自己制定规则得到的决策树,有明显的不同,因此,利用信息熵和信息增益可以得到分类效果更优的决策树。
14.决策树解决电商数据预测购买及补充问题
- 通过skleran实战
- 数据准备
- 数据处理
- 数据切分
- 准备算法
- 训练模型
- 模型预测
- 模型校验
- 模型保存
- 模型决策树可视化—export-graphviz
- 完整代码展示
import pandas as pd
#1.导入数据、
buyData=pd.read_csv("buy.csv",sep=",")
print(buyData)
# age income student credit_rating Class:buy_computer
# 0 1 3 0 1 0
# 1 1 3 0 0 0
# 2 2 3 0 1 1
# 3 3 2 0 1 1
# 4 3 1 1 1 1
# 5 3 1 1 0 0
# 6 2 1 1 0 1
# 7 1 2 0 1 0
# 8 1 1 1 1 0
# 9 3 2 1 1 1
# 10 1 2 1 0 1
# 11 2 2 0 0 1
# 12 2 3 1 1 1
# 13 3 2 0 0 0
print(buyData.shape)#(14, 5)
print(buyData.ndim) #2
# print(buyData.dtype)
print(buyData.info())
# RangeIndex: 14 entries, 0 to 13
# Data columns (total 5 columns):
# age 14 non-null int64
# income 14 non-null int64
# student 14 non-null int64
# credit_rating 14 non-null int64
# Class:buy_computer 14 non-null int64
# dtypes: int64(5)
# memory usage: 640.0 bytes
print(buyData.head())
# age income student credit_rating Class:buy_computer
# 0 1 3 0 1 0
# 1 1 3 0 0 0
# 2 2 3 0 1 1
# 3 3 2 0 1 1
# 4 3 1 1 1 1
print(buyData.index) #RangeIndex(start=0, stop=14, step=1)
print(buyData.columns)
#Index(['age', 'income', 'student', 'credit_rating', 'Class:buy_computer'], dtype='object')
#2.数据处理
X=buyData.drop(labels="Class:buy_computer",axis=1)
y=buyData["Class:buy_computer"]
#3.特征工程
#数据集切分
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=22,test_size=0.2)
# print(X_train.shape)
# print(X_test.shape)
# print(y_train.shape)
# print(y_test.shape)
#4.建立决策树模型
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier(criterion="entropy",max_depth=6,min_samples_leaf=2)#超参数
dtc.fit(X_train,y_train)
#5.模型预测
y_pred=dtc.predict(X_test)
print(y_pred) #[0 1 1]
#6.模型校验
print("model in trainset score is %.2f"%(dtc.score(X_train,y_train)))
print("model in trainset score is %.2f"%(dtc.score(X_test,y_test)))
# model in trainset score is 0.82
# model in trainset score is 0.67
from sklearn.metrics import confusion_matrix,classification_report
print("confusion matrix:",confusion_matrix(y_test,y_pred))
print("conputetion matrix:",classification_report(y_test,y_pred))
#7.保存模型
from sklearn.externals import joblib
joblib.dump(dtc,"buy.pkl")
#8.模型可视化
from sklearn.tree import export_graphviz
export_graphviz(dtc,out_file="buy.dot",feature_names=X.columns,class_names=["no","yes"],
filled=True)
- 对生成的buy.pkl进行验证 , 看是否正确
import pandas as pd
#1.导入数据、
buyData=pd.read_csv("buy.csv",sep=",")
#2.数据处理
X=buyData.drop(labels="Class:buy_computer",axis=1)
y=buyData["Class:buy_computer"]
#3.特征工程
#数据集切分
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=22,test_size=0.2)
#4.读取模型
from sklearn.externals import joblib
dtc=joblib.load("buy.pkl")
#5.模型预测
y_pred=dtc.predict(X_test)
print(y_pred) #[0 1 1]
#6.模型校验
print("model in trainset score is %.2f"%(dtc.score(X_train,y_train)))
print("model in trainset score is %.2f"%(dtc.score(X_test,y_test)))
# model in trainset score is 0.82
# model in trainset score is 0.67
from sklearn.metrics import confusion_matrix,classification_report
print("confusion matrix:",confusion_matrix(y_test,y_pred))
print("conputetion matrix:",classification_report(y_test,y_pred))
- 在生成的文件目录下打开cmd(shift+鼠标右键即可显示在此处打开命令窗口)之后执行后面的命令
dot -Tpdf .\buy.dot -o buy.pdf
15.决策树实战相亲数据集案例及可视化实战
- 将准备好的相亲数据集通过pandas进行处理
- 准备X和Y特征和标签数据
- 训练模型
- 预测模型
- 校验–可视化
import pandas as pd
file=pd.read_csv("./SklearnTest.txt")
#数据处理--is_date=
new_Date=file.query("is_date==-1")
data=file.query("is_date!=-1")
# print(new_Date)
# height house car handsome job is_date
# 8 1.65 0 1 6.6 0 -1
# print(data)
# height house car handsome job is_date
# 0 1.80 1 0 6.5 2 1
# 1 1.62 1 0 5.5 0 1
# 2 1.71 0 1 8.5 1 1
# 3 1.58 1 1 6.3 1 1
# 4 1.68 0 1 5.1 0 0
# 5 1.63 1 0 5.3 1 0
# 6 1.78 0 0 4.5 0 0
# 7 1.64 0 0 7.8 2 0
#2.将data已经处理好的数据分为X和y
X=data.drop("is_date",axis=1)
y=data["is_date"]
#3.进行切分
from sklearn.model_selection import train_test_split
#random_state=9随机数种子,如果指定随机数种子,保证每次切分的时候结果的可重复性
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=9)
#4.训练模型
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier()
dtc.fit(X_train,y_train)
print(dtc.feature_importances_)
#5.预测
y_pred=dtc.predict(X_test)
print(y_test)
#6.校验
print("model in train set score is:",dtc.score(X_train,y_train))
print("model in test set score is:",dtc.score(X_test,y_test))
from sklearn.metrics import classification_report,confusion_matrix
print("classification_report score is:",classification_report(y_test,y_pred))
print("confusion_matrix score is:",confusion_matrix(y_test,y_pred))
#可视化
from sklearn.tree import export_graphviz
export_graphviz(dtc,out_file="love.dot",feature_names=X.columns,filled=True,class_names=["no","yes"])
扩展 : 本地安装Graphviz
通过Graphviz 的地址下载该软件:http://www.graphviz.org/ , 配置本地环境变量,通过命令dot -Tpdf iris.dot -o outpu.pdf将dot文件转化至pdf可视化决策树。
class_names=["is_date:no","is_date:yes"],这里为什么指定no代表0,yes代表1呢?这是因为在class_names中默认以数值递增的顺序进行对应,也是就是0对应is_date:no.
改进相亲数据集案例
- 改进方案一
import pandas as pd
#加载数据
love_file=pd.read_csv("./SklearnTest.txt")
#数据集(切分为训练集和测试集)和新数据
data,newData=love_file.query("is_date!=-1"),love_file.query("is_date==-1")
#将数据集切分成X特征和Y类别标签
X_data=data.drop(["is_date"],axis=1)
y_data=data["is_date"]
#切分数据集
from sklearn.cross_validation import train_test_split
#random——state随机数种子-保证每一次切分数据集结果可重复性
X_train, X_test, y_train, y_test = train_test_split(X_data, y_data, test_size=0.33, random_state=1)
#建立决策树模型
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier(criterion="entropy")
#训练模型使用的是fit方法---训练模型
print(dtc.fit(X_train,y_train))
#预测新数据的结果
y_pred=dtc.predict(X_test)
#模型校验
print("model in train set score:",dtc.score(X_train,y_train))
print("model in test set score:",dtc.score(X_test,y_test))
# model in train set score: 1.0
# model in test set score: 0.3333333333333333
from sklearn.metrics import confusion_matrix
print(confusion_matrix(y_test,y_pred))
#新数据
X_new_data=newData.drop(["is_date"],axis=1) #y_new_data
print(dtc.predict(X_new_data))
#可视化处理
from sklearn.tree import export_graphviz
export_graphviz(dtc.tree_,out_file="love.dot",filled=True,feature_names=love_file.columns,class_names=["no","yes"])
- 改进方案二
import pandas as pd
#加载数据
love_file=pd.read_csv("./SklearnTest.txt")
#1.数据集(切分为训练集和测试集)和新数据
data,newData=love_file.query("is_date!=-1"),love_file.query("is_date==-1")
#将数据集切分成X特征和Y类别标签
X_data=data.drop(["is_date"],axis=1)
y_data=data["is_date"]
#2.切分数据集
from sklearn.cross_validation import train_test_split
#random——state随机数种子-保证每一次切分数据集结果可重复性
X_train, X_test, y_train, y_test = train_test_split(X_data, y_data, test_size=0.33, random_state=1)
#3.数据处理
from sklearn.preprocessing import StandardScaler
sc=StandardScaler()
#对训练数据集先进行fit操作在进行transfrom操作
#fit操作相当于收集所有参数信息,transfrom将所有的数据减去均值除以方差
X_train_std=sc.fit_transform(X_train)
#对于测试数据集来讲只需要使用transform方法进行归一化
X_test_std=sc.transform(X_test)
#4.建立决策树模型
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier(criterion="entropy")
#训练模型使用的是fit方法---训练模型
print(dtc.fit(X_train_std,y_train))
#5.预测新数据的结果
y_pred=dtc.predict(X_test)
#6.模型校验
print("model in train set score:",dtc.score(X_train_std,y_train))
print("model in test set score:",dtc.score(X_test_std,y_test))
16.决策树实战Iris数据集识别及可视化实战
- iris数据集来源于sklearn自带的数据集
- 根据自带的属性完成定义
from sklearn.datasets import load_iris
iris=load_iris()
#打印iris的基础信息
print(iris.keys()) #dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names'])
print(iris.data)
# [5.8 2.7 5.1 1.9]
# [6.8 3.2 5.9 2.3]
# [6.7 3.3 5.7 2.5]
# [6.7 3. 5.2 2.3]
# [6.3 2.5 5. 1.9]
# [6.5 3. 5.2 2.]
import numpy as np
print(np.unique(iris.target))
print(iris.target_names)#['setosa' 'versicolor' 'virginica']
print(iris.DESCR)#
print(iris.feature_names)#['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
# Data Set Characteristics:
# :Number of Instances: 150 (50 in each of three classes)
# :Number of Attributes: 4 numeric, predictive attributes and the class
# :Attribute Information:
# - sepal length in cm
# - sepal width in cm
# - petal length in cm
# - petal width in cm
# - class:
# - Iris-Setosa
# - Iris-Versicolour
# - Iris-Virginica
# :Summary Statistics:
#选择特征和标签
X=iris.data
y=iris.target
#切分数据
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=22,test_size=0.2)
#训练模型
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier()
#训练
dtc.fit(X_train,y_train)
print(dtc.feature_importances_)#[0.01672241 0. 0.59033215 0.39294544]
#预测
y_pred=dtc.predict_proba(X_test)
print(y_pred)
#验证
print("model in train set score is:",dtc.score(X_train,y_train))
print("model in test set score is:",dtc.score(X_test,y_test))
# model in train set score is: 1.0
# model in test set score is: 0.8666666666666667
#可视化
from sklearn.tree import export_graphviz
export_graphviz(dtc,out_file="iris.dot",filled=True,
class_names=iris.target_names,
feature_names=['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'],)
17.决策树算法API详解
- 参数:使用哪种算法,最大深度、树的叶子节点个数等
- 属性:
features_importance_(重要) - 方法:
fit\predict\predict_log_porba\predict_proba - 决策树文档:http://scikit-learn.org/stable/modules/tree.html#classification
- 决策树分类器的简介:http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html#sklearn.tree.DecisionTreeClassifier
- API详解
API参数详解 :
(1)criterion:一个字符串,指定切分质量的评价准则。可以为如下两个参数:
Gini:表示切分时评价准则时Gini系数。
Entropy:表示切分的时候评价准则是信息增益
(2)splitter:一个字符串,指定切分原则,可以为如下:
best:表示选择最优的切分
random:表示随机切分
(3)max_features:可以为整数、浮点、字符串或者None,指定了寻找best split时考虑的特征数量。
如果是整数,则每次切分只考虑max_features个特征。
如果是浮点数,则每次切分只考虑max_features*n_features个特征。
如果是字符串auto或者sqrt,则max_features等于sqrt(n_feautures)
如果是字符串log2,则max_features等于log2(n_features)
如果是none,则max_features等于n_features.
(4)max_depth:可以为整数或者None,指定树的最大深度。
如果为None,则表示树的深度不限(直到每个叶子都是纯的,即叶子结点中所有的样本点都属于一个类,或者叶子中包含小于min_samples_split个样本点。
(5)min_samples_split:为整数,指定每个内部节点(非叶子节点)包含的最少样本数。
(6)min_samples_leaf为整数,指定每个叶子节点包含的最少的样本数。
(7)min_weight_fraction_leaf:为浮点数,叶子结点中样本的最小权重系数。
(8)min_leaf_nodes:为整数或None,指定最大的叶节点数量。
如果为None,此时叶子节点数量不限制。
如果为非None,则max_depth被忽略。
(9)class_weight:为一个字典、字典的列表、字符串‘balanced’,或者None,它指定了分类的权重。权重的形式为:{class_label:weight}
如果是None,则每个分类的权重都为1.
字符串balanced表示分类权重是样本中各分类出现频率的反比。
(10)random_state:一个整数或者一个Randomstate实例,或者None。
如果为整数,则它指定了随机数生成器的种子。
如果为Randomstate实例,则指定了随机数生成器。
如果为None,则使用默认的随机数生成器。
(11)presort:一个布尔值,指定是否提前排序数据,从而加速寻找最优切分的过程。设置为True时,对于大数据集会减慢总体的训练过程;但是对于一个小数据集或者设定了最大深度的情况下,会加速训练过程。
API的属性详解:
(1)classes_:分类的标签值
(2)feature_importances_:给出了特征的重要程度。该值越高,则特征越重要(也称之为Gini_importance)
(3)max_feature_:max_feature的推断值。
(4)n_classes_:给出了分类的数量
(5)n_feautures_:执行fit之后特征的数量
(6)n_outputs_:执行fit之后输出的数量
(7)tree_(tree):一个Tree对象,即底层的决策树。
API的方法详解 :
(1)fit(X,y):训练模型
(2)predict(X,)用模型进行预测,返回预测值
(3)predict_log_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率的对数值。
(4)predict_proba(X):返回一个数组,数组的元素依次时X预测为各个类别的概率值。
(5)score(X,y):返回在(X,y)上预测的准确率(accurary)的平均值。
18.Python源码的ID3实现简介
- 1.ID3算法实现
from numpy import *
import math
import copy
import cPickle as pickle
class ID3DTree(object):
def __init__(self):
self.tree={}
self.dataSet=[]
self.labels=[]
def loadDataSet(self,path,labels):
recordlist = []
fp = open(path,"rb") # 读取文件内容
content = fp.read()
fp.close()
rowlist = content.splitlines() # 按行转换为一维表
recordlist=[row.split("\t") for row in rowlist if row.strip()]
self.dataSet = recordlist
self.labels = labels
def train(self):
labels = copy.deepcopy(self.labels)
self.tree = self.buildTree(self.dataSet,labels)
# 创建决策树主程序
def buildTree(self,dataSet,labels):
cateList = [data[-1] for data in dataSet] # 抽取源数据集的决策标签列
# 程序终止条件1: 如果classList只有一种决策标签,停止划分,返回这个决策标签
if cateList.count(cateList[0]) == len(cateList):
return cateList[0]
# 程序终止条件2: 如果数据集的第一个决策标签只有一个 返回这个决策标签
if len(dataSet[0]) == 1:
return self.maxCate(cateList)
# 算法核心:
bestFeat = self.getBestFeat(dataSet) # 返回数据集的最优特征轴:
bestFeatLabel = labels[bestFeat]
tree = {bestFeatLabel:{}}
del(labels[bestFeat])
# 抽取最优特征轴的列向量
uniqueVals = set([data[bestFeat] for data in dataSet]) # 去重
for value in uniqueVals:
subLabels = labels[:] #将删除后的特征类别集建立子类别集
splitDataset = self.splitDataSet(dataSet, bestFeat, value) # 按最优特征列和值分割数据集
subTree = self.buildTree(splitDataset,subLabels) # 构建子树
tree[bestFeatLabel][value] = subTree
return tree
#计算出现最多的列别标签
def maxCate(self,catelist): # 计算出现最多的类别标签
items = dict([(catelist.count(i), i) for i in catelist])
return items[max(items.keys())]
#计算最优特征
def getBestFeat(self,dataSet):
# 计算特征向量维,其中最后一列用于类别标签,因此要减去
numFeatures = len(dataSet[0]) - 1 # 特征向量维数=行向量维度-1
baseEntropy = self.computeEntropy(dataSet) # 基础熵:源数据的香农熵
bestInfoGain = 0.0; # 初始化最优的信息增益
bestFeature = -1 # 初始化最优的特征轴
# 外循环:遍历数据集各列,计算最优特征轴
# i 为数据集列索引:取值范围 0~(numFeatures-1)
for i in xrange(numFeatures): # 抽取第i列的列向量 uniqueVals = set([data[i] for data in dataSet]) # 去重:该列的唯一值集 newEntropy = 0.0 # 初始化该列的香农熵
for value in uniqueVals: # 内循环:按列和唯一值计算香农熵 subDataSet = self.splitDataSet(dataSet, i, value) # 按选定列i和唯一值分隔数据集
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * self.computeEntropy(subDataSet) infoGain = baseEntropy - newEntropy # 计算最大增益
if (infoGain > bestInfoGain): # 如果信息增益>0; bestInfoGain = infoGain
# 用当前信息增益值替代之前的最优增益值 bestFeature = i # 重置最优特征为当前列
return bestFeature
#计算信息熵
def computeEntropy(self,dataSet): # 计算香农熵
datalen = float(len(dataSet))
cateList = [data[-1] for data in dataSet] # 从数据集中得到类别标签
items = dict([(i,cateList.count(i)) for i in cateList])
# 得到类别为key,出现次数value的字典
infoEntropy = 0.0 # 初始化香农熵 for key in items: # 计算香农熵
prob = float(items[key])/datalen
infoEntropy -= prob * math.log(prob,2) # 香农熵:= - p*log2(p) --infoEntropy = -prob * log(prob,2)
return infoEntropy
# 分隔数据集:删除特征轴所在的数据列,返回剩余的数据集
# dataSet:数据集; axis:特征轴; value:特征轴的取值
def splitDataSet(self, dataSet, axis, value):
rtnList = []
for featVec in dataSet:
if featVec[axis] == value:
rFeatVec = featVec[:axis]
# list操作 提取0~(axis-1)的元素
rFeatVec.extend(featVec[axis+1:])
# list操作 将特征轴(列)之后的元素加回
rtnList.append(rFeatVec)
return rtnList
#决策树分类器代码
def predict(self,inputTree,featLabels,testVec): # 分类器
root = inputTree.keys()[0] # 树根节点
secondDict = inputTree[root] # value-子树结构或分类标签
featIndex = featLabels.index(root) # 根节点在分类标签集中的位置
key = testVec[featIndex] # 测试集数组取值
valueOfFeat = secondDict[key] #
if isinstance(valueOfFeat, dict):
classLabel = self.predict(valueOfFeat, featLabels, testVec) # 递归分类
else: classLabel = valueOfFeat
return classLabel
# 存储树到文件
def storeTree(self,inputTree,filename):
fw = open(filename,'w')
pickle.dump(inputTree,fw)
fw.close()
# 从文件抓取树
def grabTree(self,filename):
fr = open(filename)
return pickle.load(fr)
- 2.构建数据集
import sys
import os
from numpy import *
# 设置utf-8 unicode环境
reload(sys)
sys.setdefaultencoding('utf-8')
#构建输入的数据集
labels=["年龄","收入","学生","信誉"]
dataset = [[0,0,0,0,"no"],[0,0,0,1,"no"],[0,1,0,0,"no"],[0,2,1,0,"yes"],[0,1,1,1,"yes"],
[1,0,0,0,"yes"],[1,2,1,1,"yes"], [1,1,0,1,"yes"],[1,0,1,0,"yes"],[2,1,0,0,"yes"],[2,2,1,0,"yes"],
[2,2,1,1,"no"],[2,1,1,0,"yes"],[2,1,0,1,"no"]]
numlist = [64 ,64 ,128,64 ,64 ,128,64 ,32 ,32 ,60 ,64 ,64 ,132,64 ]
print mat(dataset).T
datalines =[]
for element,num in zip(dataset,numlist):
liststr =""
for cell in element:
liststr += str(cell)+"\t"
liststr = liststr[:-1]
for i in xrange(num):
datalines.append(liststr)
fp = open("dataset.dat","w")
fp.write("\n".join(datalines))
- 3.训练的决策树的结构信息打印及字典转化为树状的显示
from numpy import *
from math import log
from ID3DTree import *
import copy
import treePlotter2
import matplotlib.pyplot as plt
dtree = ID3DTree()
dtree.loadDataSet("dataset.dat",["age","revenue","student","credit"])
# dtree.loadDataSet("lenses.txt",['age','prescript','astigmatic','tearRate'])
dtree.train()
print dtree.tree
treePlotter2.createPlot(dtree.tree)
- 4.持久化决策树
from numpy import *
from math import log
from ID3DTree import *
import copy
import treePlotter2
import matplotlib.pyplot as plt
dtree = ID3DTree()
dtree.loadDataSet("dataset.dat",["age","revenue","student","credit"])
dtree.train()
dtree.storeTree(dtree.tree,"data.tree")
mytree = dtree.grabTree("data.tree")
print mytree
- 5.测试ID3算法
from numpy import *
from math import log
from ID3DTree import *
import copy
import treePlotter2
import matplotlib.pyplot as plt
dtree = ID3DTree()
labels = ["age","revenue","student","credit"]
vector = ['0','1','0','0'] # ['0','1','0','0','no']
mytree = dtree.grabTree("data.tree")
print "真实输出 ","no","->","决策树输出",dtree.predict(mytree,labels,vector)
补充 1: 基尼指数、误分类率及代码实战
-
Gini指数(基尼指数) : 选择最佳划分的度量通常是根据划分后子女节点的不纯性的程度决定的。一般最佳划分对应于产生最小Gini指标值得点。
P(i|t)表示给定节点t中属于类i的记录所占的比例。
-
错误率
![]()
以2分类问题为例计算信息熵、基尼不纯度和错误率
| 节点 | 计数 |
|---|---|
| 类=0 | 1 |
| 类=1 | 5 |
Gini=1-![]() =0.278
=0.278
Entropy=-(1/6)log(1/6)-(5/6)log(5/6)=0.650
Error=1-max[1/6,5/6]=0.167
- 信息增益公式解读
![]() 是给定节点的不纯性度量,N是父节点上的记录总数,k是属性值的个数
是给定节点的不纯性度量,N是父节点上的记录总数,k是属性值的个数![]() 是与子女节点v相关联的记录个数,决策树归纳算法通常选择最大化增益 的测试条件,因为对所有的测试条件来说,
是与子女节点v相关联的记录个数,决策树归纳算法通常选择最大化增益 的测试条件,因为对所有的测试条件来说,![]() 是一个不变的值,所以最大化增益等价于最小化子女节点的不纯性度量的的加权平均值。当选择熵作为不纯性度量时,熵的差就是所谓的信息增益。
是一个不变的值,所以最大化增益等价于最小化子女节点的不纯性度量的的加权平均值。当选择熵作为不纯性度量时,熵的差就是所谓的信息增益。
补充2:最大熵及交叉熵
底数一般为2或e
两点分布的熵
均匀分布的信息熵
定义概率:![]()
最大熵
熵是随机变量不确定性度量,不确定越大,熵越大
若随机变量退化成定值,熵最小,为0
若随机分布为均匀分布,熵最大
![]()
根据上面的分析,P(x)的对数关于随机变量x的二次形式,所以,该分布p(x)必然是正态分布。
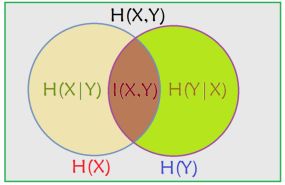
Venn图理解几个熵的概念
条件熵
两个随机变量X,Y的联合分布,可以形成联合熵H(X,Y)表示,(X,Y)发生所包含的熵,减去X单独发生的熵,就是在X发生前提下Y发生带来的熵即H(X|Y)=H(X,Y)-H(X)
利用互信息得到条件熵