（三）使用Python进行交易的随机森林算法

作者：chen_h
微信号 & QQ：862251340
微信公众号：coderpai

---

（一）机器学习中的集成学习入门

（二）bagging 方法

（三）使用Python进行交易的随机森林算法

---

在这篇文章中，我们将讨论什么是随机森林，他们如何工作，他们如何帮助克服决策树的局限性。

随着机器学习及其技术在当前环境中的蓬勃发展，越来越多的算法在各种领域中找到应用。 机器学习各个算法的工作彼此不同，其中一个算法对于某个问题可能比另一个算法更好。 机器学习算法不断更新和升级，以扩大其应用范围并最大限度地减少其缺点。

随机森林算法就是这样一种算法，旨在克服决策树的局限性。在这篇博客中，我们将介绍它。在直接介绍随机森林之前，让我们首先简要了解决策树及其工作原理。

什么是决策树？

正如其名称所示，决策树具有分层或者树状结构，其分支充当节点。我们可以通过遍历这些节点来做出某个决策，这些节点通过数据特征进行参数选择。
但是，决策树存在过度拟合的问题。 过度拟合通常在树中添加越来越多的节点来增加树内的特异性以达到某个结论，从而增加树的深度并使其更复杂。

此外，在本博客中，我们将了解 Random Forest 如何帮助克服决策树的这一缺点。

什么是随机森林？

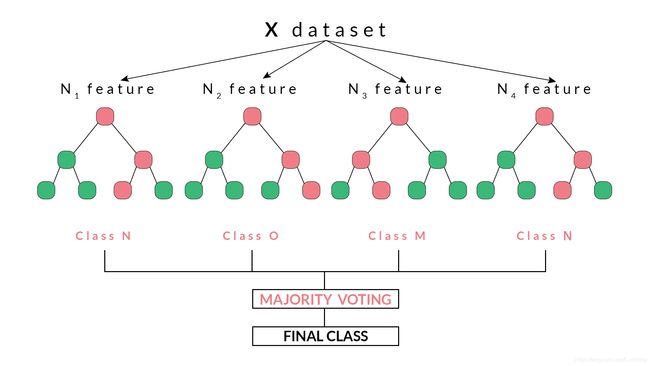
随机森林是一种使用集成方法的监督分类机器学习算法。 简而言之，随机森林由众多决策树组成，有助于解决决策树过度拟合的问题。 通过从给定数据集中选择随机特征来随机构造这些决策树。
随机森林根据从决策树收到的最大投票数得出决策或预测。 通过众多决策树达到最大次数的结果被随机森林视为最终结果。

随机森林的工作原理

随机森林基于集成学习技术，简单地表示一个组合或集合，在这种情况下，它是决策树的集合，一起称为随机森林。集合模型的准确性优于单个模型的准确性，因为它汇总了单个模型的结果并提供了最终结果。
那么，如何从数据集中选择特征以构建随机森林的决策树呢？

我们使用称为 bagging 的方法随机选择特征。根据数据集中可用的特征集，通过选择具有替换的随机特征来创建许多训练子集。这意味着可以在不同的训练子集中同时重复一个特征。

例如，如果数据集包含20个特征，并且要选择5个特征的子集来构建不同的决策树，则将随机选择这5个特征，并且任何特征都可以是多个子集的一部分。这确保了随机性，使树之间的相关性更小，从而克服了过度拟合的问题。

选择特征后，将根据最佳分割构建树。每棵树都给出一个输出，该输出被认为是从该树到给定输出的“投票”。输出

接收最大’投票’的随机森林选择最终输出/结果，或者在连续变量的情况下，所有输出的平均值被视为最终输出。

例如，在上图中，我们可以观察到每个决策树已经投票或者预测了特定的类别。随机森林选择的最终输出或类别将是N类，因为它具有多数投票或者是四个决策树中的两个预测输出。

随机森林的 Python 代码

在此代码中，我们将创建一个随机森林分类器并对其进行训练，并且给出每日回报。

导入库

import quantrautil as q
import numpy as np
from sklearn.ensemble import RandomForestClassifier

上面导入的库将按照如下方式使用：

• quantrautil：这将用于从雅虎 finance 中获取 BAC 股票的价格数据；
• numpy：对BAC股票价格执行数据操作，以计算输入特征和输出结果。如果你想要了解更多关于 numpy 的信息，可以查看 numpy 官网；
• Sklearn：sklearn 是很多工具和机器学习模型的集合，你可以很自由使用；
• RandomForestClassifier：将用于创建 Random Forest 分类器模型；

获取数据

下一步是从 quantrautil 导入 BAC 库存的价格数据。quantrautil 的 get_data 函数用于获取从 2000 年1月1日到2019年1月31日的 BAC 数据。如下所示：

data = q.get_data('BAC','2000-1-1','2019-2-1')
print(data.tail())

[*********************100%***********************]  1 of 1 downloaded
             Open   High    Low  Close  Adj Close     Volume Source
Date                                                               
2019-01-25  29.28  29.72  29.14  29.58      29.27   72182100  Yahoo
2019-01-28  29.32  29.67  29.29  29.63      29.32   59963800  Yahoo
2019-01-29  29.54  29.70  29.34  29.39      29.08   51451900  Yahoo
2019-01-30  29.42  29.47  28.95  29.07      28.77   66475800  Yahoo
2019-01-31  28.75  28.84  27.98  28.47      28.17  100201200  Yahoo

创建输入和输出数据

在这一步中，我将创建输入和输出变量。

输入变量：我使用 (open-close)/open ，(High-Low)/Low，过去5议案的标准差（std_5），过去五天的平均值(ret_5)。

输出变量：如果明天的收盘价大于今天的收盘价，则输出变量设置为 1 ，否则设置为 -1。1 表示购买股票，-1表示卖出股票。

输入和输出数据的特征完全是随机的，如果你有兴趣可以查看 wiki 。

# Features construction 
data['Open-Close'] = (data.Open - data.Close)/data.Open
data['High-Low'] = (data.High - data.Low)/data.Low
data['percent_change'] = data['Adj Close'].pct_change()
data['std_5'] = data['percent_change'].rolling(5).std()
data['ret_5'] = data['percent_change'].rolling(5).mean()
data.dropna(inplace=True)
# X is the input variable

X = data[['Open-Close', 'High-Low', 'std_5', 'ret_5']]


# Y is the target or output variable

y = np.where(data['Adj Close'].shift(-1) > data['Adj Close'], 1, -1)

训练集合和测试集合的划分

我们现在将数据集拆分为 75% 的训练数据集，25% 的测试数据集。

# Total dataset length
dataset_length = data.shape[0]
# Training dataset length

split = int(dataset_length * 0.75)

split

3597

# Splitiing the X and y into train and test datasets
X_train, X_test = X[:split], X[split:]
y_train, y_test = y[:split], y[split:]
# Print the size of the train and test dataset

print(X_train.shape, X_test.shape)

print(y_train.shape, y_test.shape)

(3597, 4) (1199, 4)
(3597,) (1199,)

训练机器学习模型

全部数据设置完毕！让我们训练一个决策树分类器模型。树中的 RandomForestClassifier 函数存储在变量 clf 中，然后使用 X_train 和 y_train 数据集作为参数调用 fit 方法，以便分类器模型可以学习输入和输出之间的关系。

clf = RandomForestClassifier(random_state=5)

# Create the model on train dataset
model = clf.fit(X_train, y_train)

from sklearn.metrics import accuracy_score
print('Correct Prediction (%): ', accuracy_score(y_test, model.predict(X_test), normalize=True)*100.0)

Correct Prediction (%):  50.29190992493745

# Run the code to view the classification report metrics
from sklearn.metrics import classification_report
report = classification_report(y_test, model.predict(X_test))
print(report)

             precision    recall  f1-score   support

         -1       0.50      0.61      0.55       594
          1       0.51      0.40      0.45       605

avg / total       0.50      0.50      0.50      1199

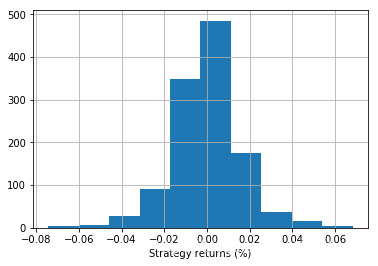
策略回报

data['strategy_returns'] = data.percent_change.shift(-1) * model.predict(X)

每日返回直方图

%matplotlib inline
import matplotlib.pyplot as plt
data.strategy_returns[split:].hist()
plt.xlabel('Strategy returns (%)')
plt.show()

策略回报

(data.strategy_returns[split:]+1).cumprod().plot()
plt.ylabel('Strategy returns (%)')
plt.show()

图中输出是根据随机森林分类器的代码显示策略回报和每日回报。

优点

• 避免过度拟合
• 可用于分类和回归
• 可以处理缺失值

缺点

• 大量的树结构会占用大量的空间和利用大量时间

在这篇博客中，我们学习了利用随机森林来进行简单的策略编写。