Myers 差分算法 (Myers Difference Algorithm) —— DiffUtils 之核心算法（一）

如果使用过 android architecture 中关于 LiveData 部分的朋友，可能对于DiffUtils这个玩意儿并不陌生。

在使用 DiffUtils 之前，如果想使用Adapter的notify系列函数，可能并不是那么方便，我们想象下，需要知道一个列表对于另外一个列表的difference，我们想简单的实现一个这种方法，并不是可以一下子写出来的。好在我们发现 Google 提供了这个工具类，就是DiffUtils。

DiffUtils.java 头部相关的介绍

    1/*
    2 * android.support.v7.util.DiffUtils
    3 *
    4 * DiffUtil uses Eugene W. Myers's difference algorithm to calculate the minimal number of updates
    5 * to convert one list into another. Myers's algorithm does not handle items that are moved so
    6 * DiffUtil runs a second pass on the result to detect items that were moved.
    7 */

这里告诉我们，DiffUtils 使用了Eugene W. Myers’s difference algorithm这个算法，我们可以简单的翻译成Myers 差分算法，来计算两个列表最小的更新操作数。在这个类的头部注释的最后，也给出了相关性能的数据：

     1/*
     2 * 

     3 *     
100 items and 10 modifications: avg: 0.39 ms, median: 0.35 ms
     4 *     
100 items and 100 modifications: 3.82 ms, median: 3.75 ms
     5 *     
100 items and 100 modifications without moves: 2.09 ms, median: 2.06 ms
     6 *     
1000 items and 50 modifications: avg: 4.67 ms, median: 4.59 ms
     7 *     
1000 items and 50 modifications without moves: avg: 3.59 ms, median: 3.50 ms
     8 *     
1000 items and 200 modifications: 27.07 ms, median: 26.92 ms
     9 *     
1000 items and 200 modifications without moves: 13.54 ms, median: 13.36 ms
    10 * 
    11 */

这个性能非常可观呀，如果结合我们的业务实际，这种计算性能，再考虑把计算操作放置到非 UI 线程中操作，那么我们得到的就是一个非常平滑的操作体验了。

Eugene W. Myers’s difference algorithm

为了致敬大神，先把大神的论文贴上：http://www.xmailserver.org/diff2.pdf

我结合源码、互联网上的文章，并摒弃一些我看不懂的内容，尽量把这一块讲明白。
首先，我们定义一个事情：

把一个列表从 A 变成 B，事实上就是找出 A 和 B 的最长公共子序列（LCS），然后把 LCS 和 A 比，多出来的删除，和 B
比，少掉的添加进去。

那么，这里的问题就演变成了如何解决这个问题了。先贴上非常重要的图

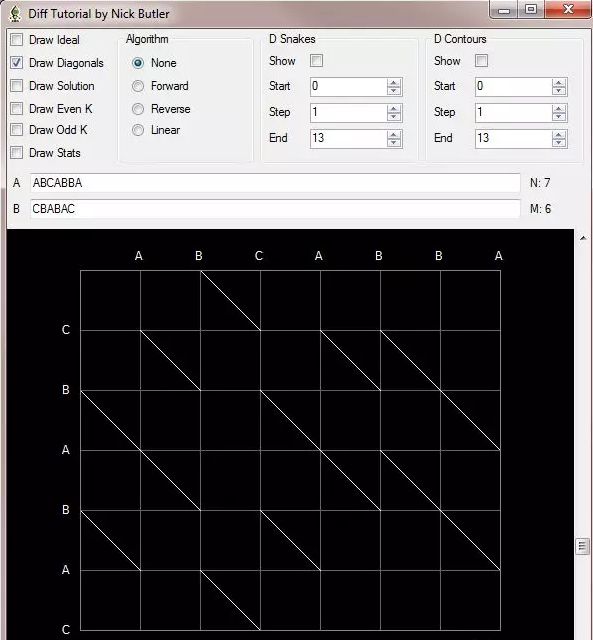
Myers Difference Algorithm

这张图，我们可以这样理解，纵坐标是序列 A，横坐标是序列 B，我们的目标是从**(0,0)走到右下角，往下走一步是删除一个 A 里面的元素，往右走一步是添加一个 B 里面的元素，往右下角走是不添加也不删除。那么问题就很简单了，我们尽量走对角边**让操作变得最少，目的是走到右下角。我们看看对角边的性质，只要 A[i] == B[j] 那么 (i,j) 就可以从 (i-1, j-1) 走过来，否则只能从 (i-1, j) 或者 (i, j-1) 走过来，所以一碰上 A[i] == B[j] 的话，就存在了一条斜边。

显然，在我们画出这幅图之后，我们有两种方式可以解题了，这幅图可以非常简单的抽象成带权重的有向图，解法是：

1. 最短路径算法，假设横向纵向权值为 1，对角权值是 0，那么只要总和权重最低，这就是我们的最优解。
2. 使用贪心算法，分解子问题，子问题的分解如上所述。

三个概念

根据 Myers 的论文，他提出了三个概念：

1. snake : 一条snake代表走一步。例如从(0,0)->(0,1) / (0,0)->(1,0) /
   (0,1)->(0,2)->(2,4) 这分别为三条snake，走对角线不计入步数。
2. k line: 定义 k = x - y （好吧，我习惯写成 y = x - k，这是相同斜率的平行斜线组成的一个集合)
3. d contour: 走一步算一个 d

上图中，我们的目标点是 （7,6)，那么k和d的关系就如下图所示了：

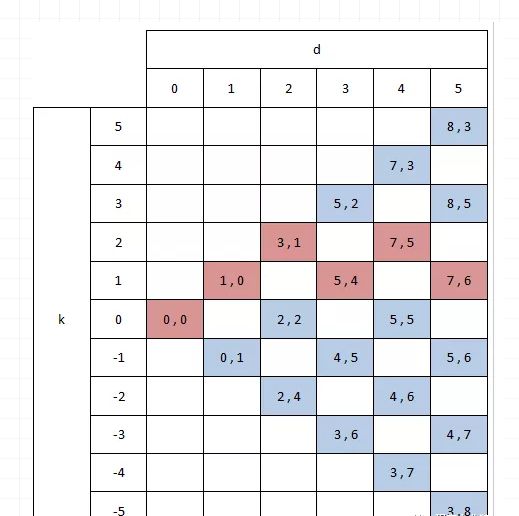
k and d

这幅图中的坐标自变量是d和k，表示了在不同d取值以及不同的k取值最终可以到达的坐标，这幅图和上面一幅图结合起来看。

当一步也不走（d = 0）的时候，我们可以“走”到最远的坐标是（0，0）; 当走一步（d = 1）的时候，我们往 k = 1 的方向走，可以走到（1，0），往 k = -1 的方向走，可以走到（0，1）

那么当走两步的时候（d = 2）的时候，我们从 k = -2 出发，起点是（2，4），往下走就到达了（2，5）这时候，发现这个点在对角线上，最终移动到（3，6）。

我们看一下，红色标记的几个方块，就是我们最终到达（7，6）的路径了，这是最优解。

结论

综上所述，我们只要能找到所有斜边，然后找到最短的d，到达我们最远的点即可。

下一篇我们讲讲 DiffUtils 里面diffPartial对该算法的实现。

免费获取安卓开发架构的资料（包括Fultter、高级UI、性能优化、架构师课程、 NDK、Kotlin、混合式开发（ReactNative+Weex）和一线互联网公司关于android面试的题目汇总可以加：936332305 / 链接：点击链接加入【安卓开发架构】：https://jq.qq.com/?_wv=1027&k=515xp64