【生成树计数】Matrix-tree定理学习笔记
学完了矩阵和行列式基础知识,终于可以去学矩阵数定理~(≧▽≦)/~
———————————–线割分是我>w<———————————————–
Matrix-tree定理,又叫Kirchhoff矩阵定理,于1847年首次被基尔霍夫先生证明,后来被广泛应用于生成树的计数问题.
要用它,需要先知道几个重要概念:
无向图的度数矩阵和邻接矩阵.
假定有无向图G,图中共有n个点.
G的度数矩阵称D[G],邻接矩阵称A[G].这两个矩阵的大小都是n*n的.
对于D[G],他满足:
di,j={0, i≠jvi的度数, i=j
而邻接矩阵就是平时用的那种i,j有边为1无边为0的那个.
然后我们定义图G的基尔霍夫矩阵C[G]=D[G]-A[G].
基尔霍夫矩阵的性质:
①对于任意一个图,他的基尔霍夫矩阵C的行列式的值为0.
因为显然基尔霍夫矩阵的每一行或者列上元素的和都是0啊= =
②如果图G不连通,其基尔霍夫矩阵的任意主子式行列式值为0.
补充:关于主子式:在一个n阶的行列式中,选取几行,再选取列号与被选行号相同的几列,这两个被选取部分相交的元素组成的新的行列式,就是原n阶行列式的i阶主子式(这个i阶主子式是一个i*i的行列式).
如:
A=⎡⎣⎢⎢⎢1231311530227543⎤⎦⎥⎥⎥
从A中找一个2阶主子式.选择的数分别是1,3那么对应的主子式就是:
A′=[1332]
既然前提是G不连通,那么我们假设G中有k个连通分量(称为 G1,⋯,Gk ).一开始这个矩阵是散乱的:
C=⎡⎣⎢⎢⎢⎢⎢Gi10⋮00Gi2⋮0⋯⋯⋱⋯00⋮Gik⎤⎦⎥⎥⎥⎥⎥
我们通过交换矩阵的行和列使得矩阵中每个G按下标顺序排列.这个过程交换次数是偶数次(行交换了x次,列必定也要交换x次),所以行列式的值不变(由之前行列式的性质).如:
C[G]=⎛⎝⎜⎜⎜⎜⎜G10⋮00G2⋮0⋯⋯⋱⋯00⋮Gk⎞⎠⎟⎟⎟⎟⎟
由于任意两个不同联通分量之间不相连,所以除了主对角线上的元素,其他元素都是0.
定义 Cr[G] 为将C[G]去掉第r行第r列剩下的那个n-1阶矩阵.
令r为第i个联通分量里的第j个顶点.这时候 Cr[G] 只是一个主子式,因此还暂时不能用性质①得到结论.
那么
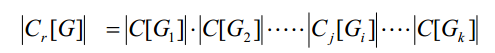
Cr[G] 不是完整矩阵,其他的 C[Gi] 是啊= =所以上面那个式子的正确性就不言而喻,性质②得证(≧▽≦)/~
③若图G是一棵树,则C[G]的任意一个n-1阶主子式的行列式的值为1.
这条性质和Matrix-tree定理本体息息相关…所以在这里写下Matrix-tree定理的内容:
G 的所有不同的生成树的个数等于其基尔霍夫矩阵C[G]任何一个 n-1 阶主子式的行列式的绝对值。
证明过程好长好长…我还没全弄明白,没法复述下来了…
贴一下论文里的图吧QAQ




到这里定理证明完毕(虽然并不是我证的> A <)
所以Matrix-tree定理也算是学完了吧…(至少知道怎么用了…第三个性质的证明以后多看几遍早晚会看懂的!0w0)