Kmeans聚类法-K均值

目录

什么是Kmeans聚类法-K均值

与系统聚类区别

K均值原理与计算

R实现

 1000个数据

10000个数据

关于聚类分析的总结

聚类分析的一些特点

---

什么是Kmeans聚类法-K均值

系统聚类法需要计算不同样品或变量的距离，当样本量很大时，会占据非常大的计算机内存空间

Kmeans是一种快速聚类法，该方法简单易懂，对计算机要求不高，

Kmeans是麦奎因提出的，基本思想是将每一个样品分配给最近中心（均值）的类中：

（1）将所有的样品分成k个初始类

（2）通过欧式距离将某个样品划入离中心最近的类中，并对获得样品与失去样品的类重新计算中心坐标。

（3）重复步骤（2），直到所有的样品都不能再分配为止。

与系统聚类区别

系统聚类对不同的类数产生一系列的聚类结果，而K均值法只能产生指定类数的聚类结果。

K均值原理与计算

Kmeans算法以k为参数，把n个对象分为k个聚类，以使聚类内具有较高的相似度，而聚类间的相似度较低，相似度的计算是根据一个聚类中对象的均值来进行的。通常采用平方误差准则，其定义如下：

其中E是数据中所有对象与相应聚类中心的均方差之和，p为代表对象空间中的一个点，mi是Ci的均值。

R实现

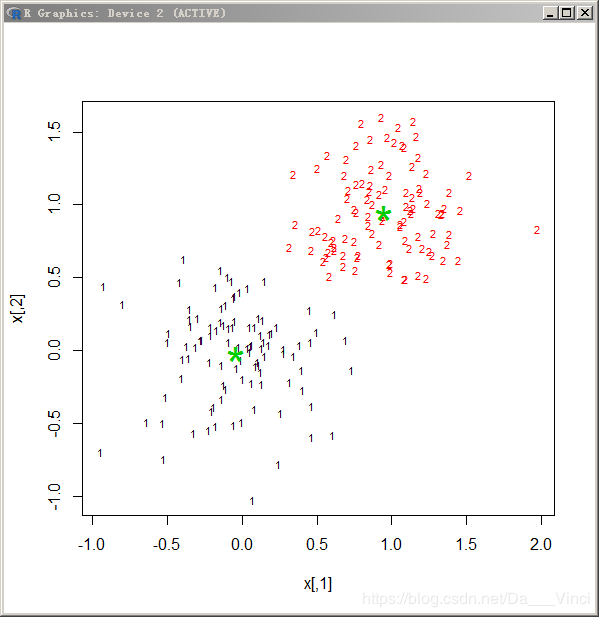
 1000个数据

x1=matrix(rnorm(1000,mean=0,sd=0.3),ncol=10)#均值1,标准差为0.3的100x10的正态随机数矩阵
x2=matrix(rnorm(1000,mean=1,sd=0.3),ncol=10) 

x=rbind(x1,x2)
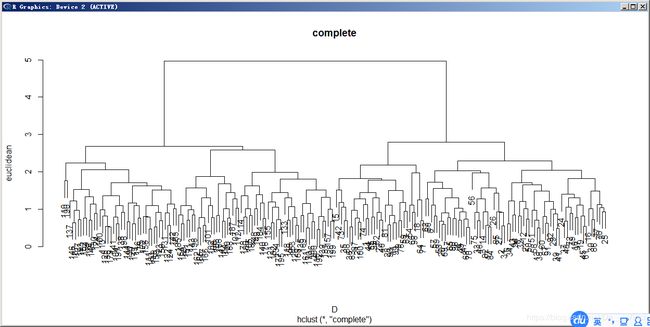
H.clust(x,"euclidean","complete")

> cl=kmeans(x,2)#kmeans聚类
> pch1=rep("1",100)
> pch2=rep("2",100)
> plot(x,col=cl$cluster,pch=c(pch1,pch2),cex=0.7)
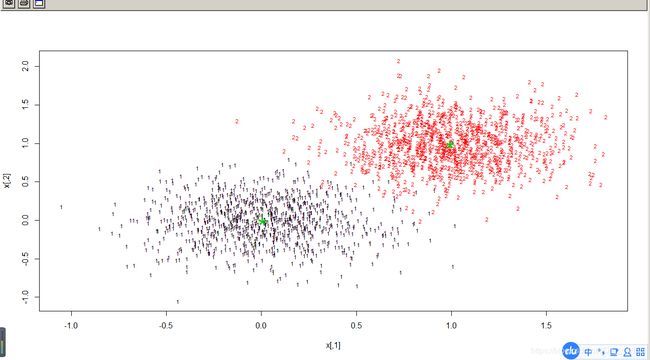
> points(cl$centers,col=3,pch="*",cex=3)

10000个数据

x1=matrix(rnorm(10000,mean=0,sd=0.3),ncol=10)#均值1,标准差为0.3的1000x10的正态随机数矩阵
x2=matrix(rnorm(10000,mean=1,sd=0.3),ncol=10) 
x=rbind(x1,x2)
cl=kmeans(x,2)#kmeans聚类
pch1=rep("1",1000)
pch2=rep("2",1000)
plot(x,col=cl$cluster,pch=c(pch1,pch2),cex=0.7)
points(cl$centers,col=3,pch ="*",cex=3)

关于聚类分析的总结

聚类分析的一些特点

（1）综合性，聚类分析可以利用多个变量信息对样品进行分类，克服单一指标分类弊端。

（2）形象性，聚类分析可以利用聚类图直观地表现其分类形态及类与类之间的内在关系

（3）客观性，聚类分析的结果克服了主观因素，比传统分类方法更客观，细致，全面和合理。