2 - 感知机(perceptron)

感知机(perceptron)是二类分类的线性分类模型，输入为实例的的特征向量，输出为实例的类别，取+1和-1二值。

感知机模型对应于输入空间（特征空间）中将训练数据进行线性划分的分离超平面，属于判别模型。感知机学习旨在求出将训练数据进行线性划分的超平面，为此导入误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。

感知机算法简单而易于实现，分为原始形式和对偶形式。

感知机是神经网络与支持向量机的基础。

1 感知机模型

输入空间 X⊆Rn ，输出空间 Y={+1,−1} 。由输入空间到输出空间的函数：

f(x)=sign(w⋅x+b)

称为感知机。其中w和b为感知机模型参数，w为权值向量(weight vector)，b为偏置(bias)，w·x表示w和x的内积(dot product)。sign是符号函数：

sign(x)={+1,x≥0−1,x<0

感知机模型是一种线性分类模型，属于判别模型。感知机模型的假设空间是定义在特征空间的所有线性分类模型(linear classification model)或线性分类器(linear classifier)，即函数集合 {f|f(x)=w⋅x+b} 。

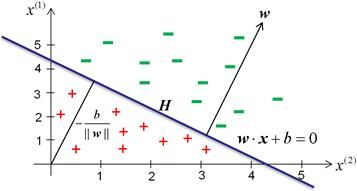
感知机的几何解释：线性方程

w⋅x+b=0

对应于特征空间 Rn 中的一个超平面，其中w是超平面的法向量，b是超平面的截距。这个超平面将特征空间划分为两个部分，位于两部分的点分布为正负两类。因此超平面S称为 分离超平面(seperating hyperplane)。

2 感知机学习策略

2.1 数据集的线性可分性

给定一个数据集，如果存在某个超平面S能够将数据集的正实例点和负实例点完全正确的划分到超平面的两侧，那么称数据集为线性可分数据集(linear separable data set)，否则，称为线性不可分。

2.2 感知机学习策略

假设训练集线性可分，感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。为了找出这样的超平面，确定参数w,b,需要确定一个学习策略，即定义loss function并将其最小化。

损失函数的一个自然地选择是误分类点的总数，但是这样的损失函数不是参数w,b的连续可导函数，不易于优化。感知机采用的是误分类点到超平面S的总距离来作为损失函数。

数学知识告诉我们，任一点 x0 到超平面S的距离：

1∥w∥|w⋅x0+b|

其中 ∥w∥ 是w的 L2 范数，即 ∥w∥=(|x1|2+|x2|2+...+|xn|2)1/2

对于我们的模型，考虑误分类点，必定有 −yi(w⋅xi+b)>0 成立(注意 yi 取值为 ±1 )。因此误分类点到超平面的距离为:

−1∥w∥yi(w⋅xi+b)

这样，所有误分类点到超平面的总距离为：

−1∥w∥∑xi∈Myi(w⋅xi+b)

不考虑 1∥w∥ ，就得到了感知机学习的损失函数。

给定训练集 T={(x1,y1),(x2,y2),...,(xN,yN)} ，其中， xi∈Rn ， y∈{+1,−1} 。感知机sign(w·x +b) 学习的损失函数定义为：

L(w,b)=−∑xi∈Myi(w⋅x+b)

其中，M为 误分类点的集合。这就是感知机学习的经验风险损失函数。

3 感知机学习算法

经过上面讨论，感知机学习问题现在变为损失函数最优化问题，最优化的方法是随机梯度下降法。

3.1 感知机学习算法的原始形式

现在要求参数w,b，使其为以下损失函数极小化问题的解：

minL(w,b)=−∑xi inMyi(w⋅xi+b)

其中M为误分类点的集合。

感知机学习是误分类推动的，具体采用随机梯度下降法(stocastic gradient descent，SGD)。首先，选取初始值 w0,b0 ，然后采用梯度下降法不断地极小化目标函数，极小化过程不是一次使M中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。

以上损失函数L(w,b)对w和b求偏导可得：

∇wL(w,b)=−∑xi∈Myixi∇bL(w,b)=−∑xi∈Myi

这便是损失函数的梯度，据此我们可以对w,b进行更新。

随机选择一个误分类点 (xi,yi) ，对w,b进行更新：

w←w+ηyixib←b+ηyi

其中 η(0<η≤1) 是步长，又称为学习率(learning rate)。这样就能使L不断减小，直到0。

算法：感知机学习算法的原始形式：
输入：线性可分的训练数据集 T={(x1,y1),(x2,y2),...,(xN,yN)} ，其中 xi∈Rn ， yi∈{+1,−1} ，i = 1, 2, … , N ; 学习率 η(0<η≤1)
输出：w,b；感知机学习模型 f(x)=sign(w⋅x+b)

(1)选取初值 w0,b0
(2)在训练集中选取数据 (xi,yi)
(3)如果 yi(w⋅xi+b)≤0

w←w+ηyixib←b+ηyi

(4)转至(2)，直至训练集中没有误分类点

算法直观上的解释：当一个点被误分类，则调整w,b的值，使分离超平面向该误分类点的一侧移动，以减少该误分类点与超平面之间的距离，直至超平面越过该误分类点使其被正确分类。

值得注意的是，感知机学习算法由于采用不同的初值或选取不同的误分类点，解可以不同。

可以证明，对于线性可分数据集，感知机学习算法原始形式收敛，即经过有限次迭代可以得到一个将训练集完全正确划分的分离超平面及感知机模型。

3.2 感知机学习算法的对偶形式

感知机(perceptron)学习算法的原始形式和对偶形式与支持向量机(SVM)的原始形式和对偶形式相对应。

对偶形式基本思想：将w,b 表示为 xi,yi 的线性组合的形式，通过求解系数而得到w和b。

假设 w0,b0 初值均为0，对于误分类点 (xi,yi) 通过

w←w+ηyixib←b+ηyi

逐步修改w,b ，设修改n次，则w,b关于 (xi,yi) 的增量分别是 αiyixi 和 αiyi ，这里 αi=niη ，这样，可以看出最后学习到的w,b可以表示为：

w=∑i=1Nαiyixib=∑i=1Nαiyi

这里， αi≥0 ，当 η=1 时，表示 第i个实例点由于误分类而进行更新的次数。

算法：感知机学习算法的对偶形式
输入：线性可分的训练数据集 T={(x1,y1),(x2,y2),...,(xN,yN)} ，其中 xi∈Rn ， yi∈{+1,−1} ，i = 1, 2, … , N ; 学习率 η(0<η≤1)
输出： α ,b；感知机学习模型 f(x)=sign(∑j=1N(αjyjxj⋅x)+b) ，其中 α=(α1,α2,...,αN)T
(1) α=0,b=0
(2)在训练集中选取数据 (xi,yi)
(3)如果 yi(∑j=1N(αjyjxj⋅xi)+b)≤0

αi←αi+ηb←b+ηyi

(4)转至(2)直至没有误分类数据

对偶形式中的训练实例仅以内积形式出现，为了方便，可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储，这个矩阵就是所谓的Gram矩阵：

G=[xi⋅xj]N×N

一些理解上的提示：

• ∑j=1N(αjyjxj⋅xi) 代表向量 α 与Gram矩阵的第i列的内积
• 若对 xi 点进行更新，那么 αi=αi+1,b=b+yi(η=1)