【深度学习】基于im2col的展开Python实现卷积层和池化层

一、回顾

上一篇 我们介绍了，卷积神经网的卷积计算和池化计算，计算过程中窗口一直在移动，那么我们如何准确的取到窗口内的元素，并进行正确的计算呢？

另外，以上我们只考虑的单个输入数据，如果是批量数据呢？

首先，我们先来看看批量数据，是如何计算的

二、批处理

在神经网络的处理中，我们一般将输入数据进行打包批处理，通过批处理，能够实现处理的高效化和学习时对mini-batch的对应

自然，我们也希望在卷积神经网络的卷积运算中也使用批处理，为此，需要将在各层间传递的数据保存为四维数据

如上图

• 输入数据：批数目为3，通道为3
• 卷积核：数目为3，通道为3
• 输出数据：数目为3，通道为1

三、四维数据

如上所述，CNN中各层将传递的数据是四维数据，例如：

• 数据形状为(10,1,28,28)，表示10个高为28，长为28，通道为1的数据

CNN中处理四维数据，按照以上的操作会很复杂，但是通过im2col这个技巧，就会变得很简单

四、im2col

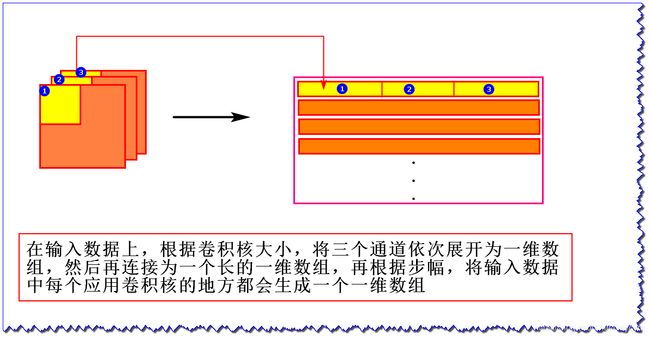
• 对于输入数据

• 对于卷积核
  

输入数据展开以适合卷积核（权重）

• 输入数据，将应用卷积核的区域（3维数据）横向展开为一行
• 卷积核，纵向展开为1列
• 计算乘积即可

• 批量计算
  

五、python实现im2col和col2im

• np.pad()函数

import numpy as np

A = np.arange(1,5).reshape(2,2)  # 将1,2,3,4转换为2*2的矩阵
print(A)

B = np.pad(A,((1,1),(2,2)),'constant')  
# ((1,1),(2,2))
# 对A矩阵进行扩充，(1,1)表示上下各加一行，(2,2)左右各加两列
print(B)

输出为：
[[1 2]
 [3 4]]
 
[[0 0 0 0 0 0]
 [0 0 1 2 0 0]
 [0 0 3 4 0 0]
 [0 0 0 0 0 0]]

1、im2col

import numpy as np

def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    """
    Parameters
    ----------
    input_data : 由(数据量, 通道, 高, 长)的4维数组构成的输入数据
    filter_h : 卷积核的高
    filter_w : 卷积核的长
    stride : 步幅
    pad : 填充

    Returns
    -------
    col : 2维数组
    """
    # 输入数据的形状
    # N：批数目，C：通道数，H：输入数据高，W：输入数据长
    N, C, H, W = input_data.shape  
    out_h = (H + 2*pad - filter_h)//stride + 1  # 输出数据的高
    out_w = (W + 2*pad - filter_w)//stride + 1  # 输出数据的长
    # 填充 H,W
    img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
    # (N, C, filter_h, filter_w, out_h, out_w)的0矩阵
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
    
    for y in range(filter_h):
        y_max = y + stride*out_h
        for x in range(filter_w):
            x_max = x + stride*out_w
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
    # 按(0, 4, 5, 1, 2, 3)顺序，交换col的列，然后改变形状
    col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
    return col

# 测试
x = np.random.rand(3, 3, 4, 4) # 随机数生成
print(im2col(x,2,2,2,0))
print(im2col(x,2,2,2,0).shape)

输出为：
[[0.8126537  0.0124403  0.98329453 0.57534957 0.01075175 0.28476833 0.55240652 0.71247792 0.8866451  0.08312604 0.82491841 0.53558742]
 [0.29177981 0.50891739 0.58534285 0.18979016 0.82281101 0.82324137 0.56737161 0.31075336 0.02638588 0.63497472 0.32696265 0.96400363]
 [0.18770887 0.80279488 0.80743415 0.01885739 0.6043541  0.1325915 0.99802281 0.70238769 0.03320778 0.21225932 0.73413182 0.68671415]
 [0.63299868 0.71823646 0.81703541 0.20652069 0.05803092 0.78660436 0.86116481 0.24152935 0.75596431 0.97947061 0.84386563 0.53657106]
 [0.77410888 0.92973798 0.42845759 0.20494453 0.55320755 0.86069213 0.14749488 0.5110566  0.19249778 0.38564893 0.78868462 0.49548582]
 [0.28778559 0.67286705 0.6351968  0.50743453 0.42905218 0.20382354 0.04566382 0.32610886 0.60199126 0.21139752 0.06912991 0.69890244]
 [0.03473951 0.67443498 0.53320896 0.44542062 0.96787968 0.92660522 0.8726162  0.54056736 0.62510367 0.12935292 0.35858458 0.88899527]
 [0.08295843 0.86116853 0.11507337 0.27507467 0.43662151 0.23341227 0.66133038 0.32065362 0.07386012 0.45717299 0.00857706 0.26429706]
 [0.5203922  0.79072121 0.0861702  0.64400793 0.76287695 0.53397396 0.61997931 0.88647105 0.07416818 0.23701745 0.91067976 0.14036269]
 [0.92652241 0.90052592 0.28945134 0.10758509 0.66142524 0.81998174 0.29023353 0.10070337 0.84680753 0.38787205 0.62224245 0.25184519]
 [0.00896273 0.86085848 0.72448385 0.97710942 0.27221302 0.30631167 0.80608232 0.92652234 0.35904511 0.26833127 0.72821478 0.72382557]
 [0.31399633 0.12624691 0.37392867 0.71121627 0.98641763 0.01551433 0.82284883 0.67615753 0.21826556 0.90338993 0.41159445 0.98961608]]
(12, 12)

我们设置如上图中的形状

• 输入数据：(3,3,4,4)
• 卷积核：(2,2)
• 结果为：(12,12)

结果和图中的结果一样，12行（3个数据，每个数据4行），每行有12个元素（应用(2,2)卷积核1次，三个通道，322=12）

2、col2im

def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
    N, C, H, W = input_shape
    out_h = (H + 2*pad - filter_h)//stride + 1
    out_w = (W + 2*pad - filter_w)//stride + 1
    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)

    img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
    for y in range(filter_h):
        y_max = y + stride*out_h
        for x in range(filter_w):
            x_max = x + stride*out_w
            img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]

    return img[:, :, pad:H + pad, pad:W + pad]

六、实现卷积层

class Convolution:
	# 初始化权重（卷积核4维）、偏置、步幅、填充
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
        
        # 中间数据（backward时使用）
        self.x = None   
        self.col = None
        self.col_W = None
        
        # 权重和偏置参数的梯度
        self.dW = None
        self.db = None

    def forward(self, x):
        # 卷积核大小
        FN, C, FH, FW = self.W.shape
        # 数据数据大小
        N, C, H, W = x.shape
        # 计算输出数据大小
        out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
        out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
        # 利用im2col转换为行
        col = im2col(x, FH, FW, self.stride, self.pad)
        # 卷积核转换为列，展开为2维数组
        col_W = self.W.reshape(FN, -1).T
        # 计算正向传播
        out = np.dot(col, col_W) + self.b
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

        self.x = x
        self.col = col
        self.col_W = col_W

        return out

    def backward(self, dout):
        # 卷积核大小
        FN, C, FH, FW = self.W.shape
        dout = dout.transpose(0,2,3,1).reshape(-1, FN)

        self.db = np.sum(dout, axis=0)
        self.dW = np.dot(self.col.T, dout)
        self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)

        dcol = np.dot(dout, self.col_W.T)
        # 逆转换
        dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)

        return dx

七、实现池化层

class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad
        
        self.x = None
        self.arg_max = None

    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)
		# 展开
        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
        col = col.reshape(-1, self.pool_h*self.pool_w)
		# 最大值
        arg_max = np.argmax(col, axis=1)
        out = np.max(col, axis=1)
        # 转换
        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)

        self.x = x
        self.arg_max = arg_max

        return out

    def backward(self, dout):
        dout = dout.transpose(0, 2, 3, 1)
        
        pool_size = self.pool_h * self.pool_w
        dmax = np.zeros((dout.size, pool_size))
        dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
        dmax = dmax.reshape(dout.shape + (pool_size,)) 
        
        dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
        dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
        
        return dx

总结

• 本篇的难点在于数据的展开和逆转换
• 关于卷积层和池化层的计算也比较好理解，但是代码实现有点绕，不过原理和神经网络中的全连接层实现方式一样