卷积神经网络基础 -- DeepLearning.ai 学习笔记(4-1)
课程笔记地址:https://blog.csdn.net/column/details/26931.html
课程代码地址:https://github.com/duboya/DeepLearning.ai-pragramming-code/tree/master
欢迎大家fork及star!(-O-)
卷积神经网络 — 卷积神经网络基础
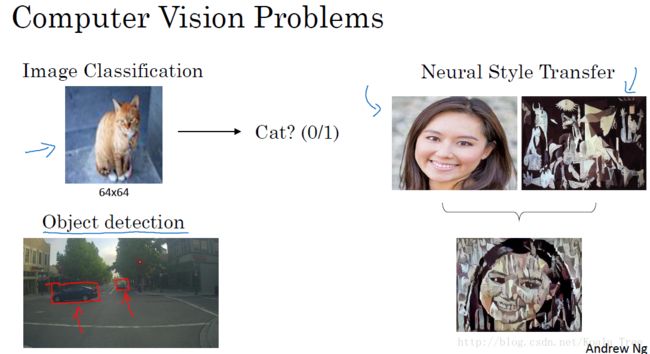
1. 计算机视觉
计算机视觉(Computer Vision)包含很多不同类别的问题,如图片分类、目标检测、图片风格迁移等等。
对于小尺寸的图片问题,也许我们用深度神经网络的结构可以较为简单的解决一定的问题。但是当应用在大尺寸的图片上,输入规模将变得十分庞大,使用神经网络将会有非常多的参数需要去学习,这个时候神经网络就不再适用。
卷积神经网络在计算机视觉问题上是一个非常好的网络结构。
2. 边缘检测示例
卷积运算是卷积神经网络的基本组成部分。下面以边缘检测的例子来介绍卷积运算。
所谓边缘检测,在下面的图中,分别通过垂直边缘检测和水平边缘检测得到不同的结果:
垂直边缘检测:
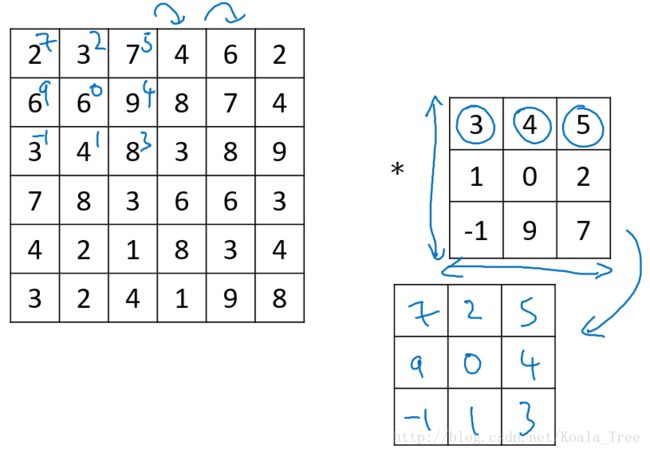
假设对于一个 6×6 大小的图片(以数字表示),以及一个 3×3 大小的 filter(卷积核) 进行卷积运算,以“*”符号表示。图片和垂直边缘检测器分别如左和中矩阵所示:
filter 不断地和其大小相同的部分做对应元素的乘法运算并求和,最终得到的数字相当于新图片的一个像素值,如右矩阵所示,最终得到一个 4×4 大小的图片。
边缘检测的原理:
以一个有一条垂直边缘线的简单图片来说明。通过垂直边缘 filter 我们得到的最终结果图片可以明显地将边缘和非边缘区分出来:
卷积运算提供了一个方便的方法来检测图像中的边缘,成为卷积神经网络中重要的一部分。
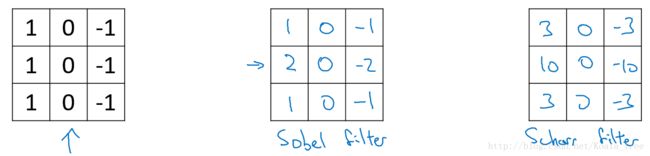
多种边缘检测:
垂直和水平边缘检测
更复杂的filter
对于复杂的图片,我们可以直接将filter中的数字直接看作是需要学习的参数,其可以学习到对于图片检测相比上面filter更好的更复杂的filter,如相对于水平和垂直检测器,我们训练的 filter 参数也许可以知道不同角度的边缘。
通过卷积运算,在卷积神经网络中通过反向传播算法,可以学习到相应于目标结果的filter,将其应用于整个图片,输出其提取到的所有有用的特征。
卷积和互相关:
在数学定义上,矩阵的卷积(convolution)操作为首先将卷积核同时在水平和垂直方向上进行翻转,构成一个卷积核的镜像,然后使用该镜像再和前面的矩阵进行移动相乘求和操作。如下面例子所示:
在深度学习中,我们称为的卷积运算实则没有卷积核变换为镜像的这一步操作,因为在权重学习的角度,变换是没有必要的。深度学习的卷积操作在数学上准确地来说称为互相关(cross-correlation)。
3. Padding
没有Padding的缺点:
-
每次卷积操作,图片会缩小;
就前面的例子来说,6×6 大小的图片,经过 3×3 大小的 filter,缩小成了 4×4大小
图片: n × n − > ( n − f + 1 ) × ( n − f + 1 ) n \times n -> (n - f + 1) \times (n - f + 1) n×n−>(n−f+1)×(n−f+1) -
角落和边缘位置的像素进行卷积运算的次数少,可能会丢失有用信息。
其中,n表示图片的长或宽的大小,f表示filter的长或宽的大小。
加Padding:
为了解决上面的两个缺点,我们在进行卷积运算前为图片加padding,包围角落和边缘的像素,使得通过filter的卷积运算后,图片大小不变,也不会丢失角落和边沿的信息。
以p表示 Padding 的值,则输入n×n大小的图片,最终得到的图片大小为 ( n + 2 p − f + 1 ) × ( n + 2 p − f + 1 ) (n + 2p − f + 1) × (n + 2p − f + 1) (n+2p−f+1)×(n+2p−f+1),为使图片大小保持不变,需根据filter的大小调整p的值。
Valid / Same 卷积:
-
Valid:no padding; ( n × n − > ( n − f + 1 ) × ( n − f + 1 ) ) (n \times n -> (n - f + 1) \times (n - f + 1)) (n×n−>(n−f+1)×(n−f+1))
-
Same:padding,输出与输入图片大小相同,( p = ( f − 1 ) / 2 p = (f − 1) / 2 p=(f−1)/2)。在计算机视觉中,一般来说padding的值为奇数(因为filter一般为奇数)
即通过n + 2p - f + 1 = n,即保持卷积前后输入输出图片大小相同,得到 p = ( f − 1 ) 2 p = \frac{(f - 1)}{2} p=2(f−1)。
4. 卷积步长(stride)
卷积的步长是构建卷积神经网络的一个基本的操作。
如前面的例子中,我们使用的 stride=1,每次的卷积运算以1个步长进行移动。下面是 stride=2 时对图片进行卷积的结果:
以s表示stride的大小,那么在进行卷积运算后,图片的变化为:
n × n − > ⌊ n + 2 p − f s + 1 ⌋ × ⌊ n + 2 p − f s + 1 ⌋ n \times n -> \lfloor \frac{n + 2p -f}{s} + 1\rfloor \times \lfloor \frac{n + 2p -f}{s} + 1\rfloor n×n−>⌊sn+2p−f+1⌋×⌊sn+2p−f+1⌋
注意,在当padding ≠ \neq ̸= 1,若移动的窗口落在图片外面时,则不要再进行相乘的操作,丢弃边缘的数值信息,所以输出图片的最终维度为向下取整。
5. 立体卷积
卷积核的通道数:
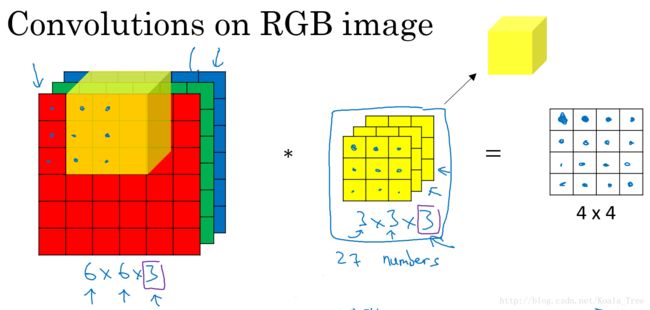
对于灰色图像中,卷积核和图像均是二维的。而应用于彩色图像中,因为图片有R、G、B三个颜色通道,所以此时的卷积核应为三维卷积核。
卷积核的第三个维度需要与进行卷积运算的图片的通道数相同。
多卷积核:
单个卷积核应用于图片时,提取图片特定的特征,不同的卷积核提取不同的特征。如两个大小均为 3 × 3 × 3 3 \times 3 \times 3 3×3×3 的卷积核分别提取图片的垂直边缘和水平边缘。
由图可知,最终提取到彩色图片的垂直特征图和水平特征图,得到有2个通道的4×4大小的特征图片。
Summary:
图片:
( n × n × n c ) ∗ ( f × f × n c ) − > ( n − f + 1 ) × ( n − f + 1 ) × n c ′ (n \times n \times n_c) * (f \times f \times n_c) -> (n - f + 1) \times (n - f + 1) \times n_c^{'} (n×n×nc)∗(f×f×nc)−>(n−f+1)×(n−f+1)×nc′
其中, n c n_c nc表示当前图片通道(channel)的数量, n c ′ n_c^{'} nc′表示下一层的通道数,同时也等于本层卷积核的个数。
6. 简单卷积网络
单层卷积网络的例子:
和普通的神经网络单层前向传播的过程类似,卷积神经网络也是一个先由输入和权重及偏置做线性运算,然后得到的结果输入一个激活函数中,得到最终的输出:
z [ 1 ] = w [ 1 ] a [ 0 ] + b [ 1 ] a [ 1 ] = g ( z [ 1 ] ) z^{[1]} = w^{[1]}a^{[0]} + b^{[1]}\\ a^{[1]} = g(z^{[1]}) z[1]=w[1]a[0]+b[1]a[1]=g(z[1])
不同点是在卷积神经网络中,权重和输入进行的是卷积运算。
注:是一个卷积核对应一个bias(不是一个卷积核的一个通道(channel)对应一个bias),所以有多少卷积核就有多少bias。
单层卷积的参数个数:
在一个卷积层中,如果我们有10个 3 × 3 × 3 3 \times 3 \times 3 3×3×3 大小的卷积核,那么加上每个卷积核对应的偏置,则对于一个卷积层,我们共有的参数个数为:
( 3 × 3 × 3 + 1 ) × 10 = 280 (3 \times 3 \times 3 + 1) \times 10 = 280 (3×3×3+1)×10=280
注:是一个卷积核(不是每层3x3对应一个bias)才对应一个bias
无论图片大小是多少,该例子中的卷积层参数个数一直都是280个,相对于普通的神经网络,卷积神经网络的参数个数要少很多。
标记的总结:
简单卷积网络示例:
多层卷积构成卷积神经网络,下面是一个卷积神经网络的例子:
卷积网络层的类型:
-
卷积层(Convolution),Conv
-
池化层(Pooling),Pool
-
全连接层(Fully connected):Fc
7. 池化层
最大池化(Max pooling):
最大池化是对前一层得到的特征图进行池化减小,仅由当前小区域内的最大值来代表最终池化后的值。
在最大池化中,有一组超参数需要进行调整,其中, f f f 表示池化的大小, s s s表示步长。
-
池化前: n × n n \times n n×n;
-
池化后: ⌊ n + 2 p − f s + 1 ⌋ × ⌊ n + 2 p − f s + 1 ⌋ \lfloor \frac{n + 2p -f}{s} + 1 \rfloor \times \lfloor \frac{n + 2p -f}{s} + 1\rfloor ⌊sn+2p−f+1⌋×⌊sn+2p−f+1⌋
平均池化(Average pooling):
平均池化与最大池化唯一不同的是其选取的是小区域内的均值来代表该区域内的值。
- 平均池化没有最大池化流行,平均池化会带来图像模糊。
- 池化一般是f = 2, s =2,即图像尺寸上缩小为原来的一半(长、宽),但通道(channel)并不会发生变化。
池化 Summary:
池化层的超参数:
-
f:filter的大小;
-
s:stride大小;
-
最大池化或者平均池化;
-
p:padding,这里要注意,几乎很少使用。
注意,池化层没有需要学习的参数,所以一般不会将池化层看做单独的一层,而是将其与卷基层归为一层。
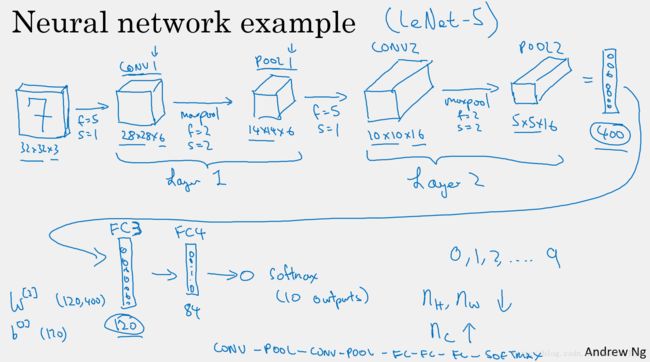
8. 卷积神经网络示例
这里以 LeNet-5 为例,给出一个完整的卷积神经网络。
构建深度卷积的模式:
-
随着网络的深入,提取的特征图片大小将会逐渐减小,但同时通道数量应随之增加;
-
Conv——Pool——Conv——Pool——Fc——Fc——Fc——softmax。
上面从conv-Fc过度过程时将神经元平铺这一步骤是不算到层次划分的,默认Pool-Fc或者Conv-FC时自动完成。
对于卷积神经网络,有两种划分层次方法:
(1) 将pool层当做独立的一层;
(2)不将pool层当做独立的一层,而是将其与conv层合在一起称为一层,因为pool层没有参数,只有几个超参数;Ng也是采用第二种方式:即将pool层与conv层合在一起称为一层,不将pool层单独划分层。
卷积神经网络的参数:
根据上表我们可以看出,对于卷积卷积神经网络的参数:
- 在卷积层,仅有少量的参数;
- 在池化层,没有参数;
- 在全连接层,存在大量的参数。
- 上面各层参数计算是有问题的,拿CONV1举例,其实际参数量应该是
( f × f × i n p u t _ c h a n n e l + 1 ) × n u m b e r _ o f _ f i l t e r s = ( 5 × 5 × 3 + 1 ) × 8 = 608 (f \times f \times input\_channel + 1) \times number\_of\_filters = (5\times5\times3 + 1) \times 8 = 608 (f×f×input_channel+1)×number_of_filters=(5×5×3+1)×8=608,
即便是不考虑bias,那也是 5 ∗ 5 ∗ 3 ∗ 8 = 600 5*5*3*8=600 5∗5∗3∗8=600,而上图计算过程中却是没有考虑input_channel,其结果208 = (5 * 5 + 1) * 8,这样是有问题的,毕竟不是拿各单层filter对应input的各channel。
注:Ng没有错,因为这个针对的是LeNet-5,而LeNet-5是针对灰度图的,即原始输入为: n h ∗ n w ∗ 1 n_h * n_w * 1 nh∗nw∗1,chanel只有一个灰度层,不是RGB,所以这里参数仍然是:
( 5 × 5 × 1 + 1 ) × 8 = 208 (5 \times 5 \times 1 + 1) \times 8 = 208 (5×5×1+1)×8=208,没有错!- Activation size大小总体呈下降趋势,但是速度不能太快,不然也会影响最终模型表现。
9. 使用卷积神经网络
参数少的优势:
与普通的全连接神经网络相比,卷积神经网络的参数更少。如图中的例子,卷积神经网络仅有 6 × ( 5 × 5 + 1 ) = 156 6 \times (5 \times 5 + 1) = 156 6×(5×5+1)=156个参数,而普通的全连接网络有 3072 × 4704 ≈ 14 M 3072 \times 4704 \approx 14M 3072×4704≈14M个参数。
-
参数共享:一个特征检测器(filter)对图片的一部分有用的同时也有可能对图片的另外一部分有用。
-
连接的稀疏性:在每一层中,每个输出值只取决于少量的输入。
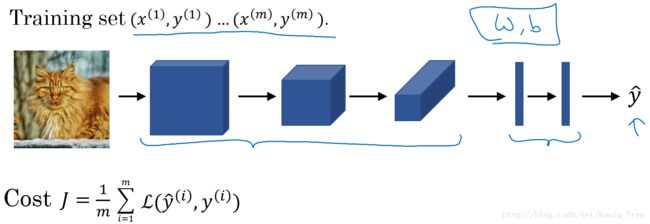
训练卷积神经网络:
我们将训练集输入到卷积神经网络中,对网络进行训练。利用梯度下降(Adam、momentum等优化算法)最小化代价函数来寻找网络最优的参数。
注:参考补充自:
https://blog.csdn.net/koala_tree/article/details/78458067