【线段树详解】从入门到各种实用技巧

入门级:

引入

让我们先来看一道模板题：洛谷P1816
题意大致是： 维护一个长度为$n$的序列，要支持查询任意区间最小值
暴力的代码非常好写出,时间复杂度是$O(N^2)$的，肯定会TLE

那么这时候我们的线段树就派上用场了

正题

1: 线段树的结构

线段树，就自然是树形结构了，并且是一颗二叉树
一颗维护长度为$8$的序列的线段树长下面这个样子

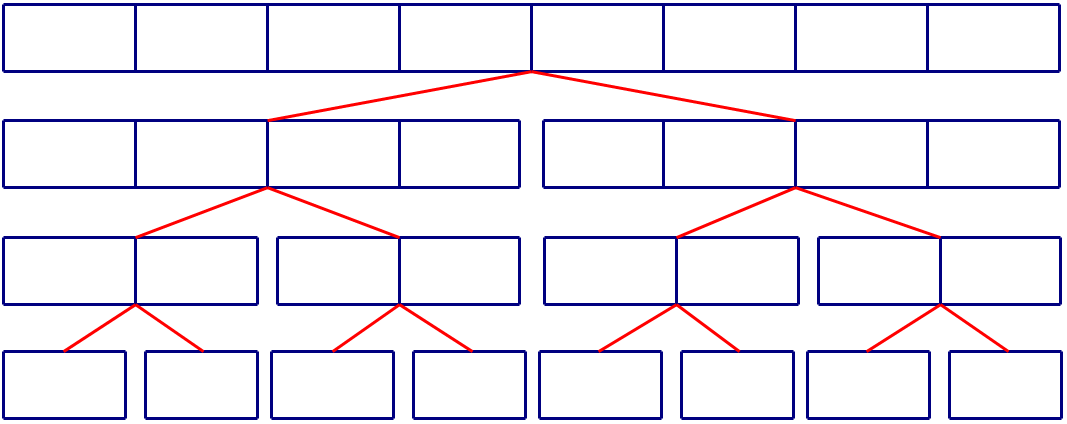
其中深度为$1$的结点维护区间$[1,8]$的值，深度为$2$的两个节点分别维护区间$[1,4]$和从区间$[5,8]$的值，依次列推
一个节点如果维护区间$[l,r]$的值，那么它的左儿子维护的就是从区间$[l,(l+r)/2]$的值，右儿子维护的就是区间$[(l+r)/2+1,r]$的值
这样，一颗维护区间$[1,n]$的线段树的深度不会超过$\lceil {\log }_2(n)\rceil +1$
那么，值就非常好维护了

1. 叶子节点的值是它自己本身的值
2. 非叶子结点的值是它的左右儿子的值经过题目要求的处理后得到的
   这样，构建一颗线段树就很容易了
   还有一个细节需要注意：如果一个节点的编号为$x$，那么它的左儿子的编号为$2x$，右儿子的编号为$2x+1$，具体为什么的话，这是为了方便查找，也方便理解，代码写多了自然能体会到好处
   具体实现详见代码，以下是维护区间最小值的线段树构建的代码,时间复杂度$O(N)$

void build(int now,int l,int r){
	if(l==r){//当l==r时，当前点是叶子节点
		cnt++;
		minn[now]=a[cnt];//minn[now]为当前结点维护的区间的值
		                 //a[cnt]为当前叶子结点的值
	}else{
		int mid=(l+r)/2;
		build(now*2,l,mid);
		build(now*2+1,mid+1,r);
		minn[now]=min(minn[now*2],minn[now*2+1]);
	}
}

2: 线段树的单点修改

由于是单点修改，我们只需要找到点的位置，修改后，在回溯过程中在维护到根的路径上的点的值，思路算是非常清晰了，时间复杂度$O(\log N)$
上代码：

void update(int now,int l,int r,int x,int y){//把编号为x的点的值修改成y
	if(l==r)minn[now]=y;else{
		int mid=(l+r)/2;
		if(x<=mid)update(now*2,l,mid,x,y);else
		if(x>mid)update(now*2+1,mid+1,r,x,y);
		minn[now]=min(minn[now*2],minn[now*2+1]);
	}
}

3: 线段树区间查询

这里线段树的优越性就体现出来了
暴力的查询是$O(N)$的，但是我们是用了线段树，已经维护了某一些区间的值，就不需要在去查询这些区间的是，而是直接使用我们维护到的值
比如我们查询区间$[3,7]$,我们就可以把它拆成$[3,4],[5,6],[7,7]$，查询区间$[4,8]$,就可以拆成$[4,4],[5,8]$,依然是通过递归的方式实现，时间复杂度$O(\log N)$

int get_min(int now,int l,int r,int q_l,int q_r){//查询[q_l,q_r]的最小值
	int re=0x7fffffff;
	if(q_l<=l&&q_r>=r){//如果查询区间把当前区间覆盖
		re=minn[now];
	}else{
		int mid=(l+r)/2;
		if(q_l<=mid)re=min(re,get_min(now*2,l,mid,q_l,q_r));
		//如果查询区间与左儿子的区间有交集，查询左儿子的区间
		if(q_r>mid)re=min(re,get_min(now*2+1,mid+1,r,q_l,q_r));
		//如果查询区间与右儿子的区间有交集，查询右儿子的区间
	}
	return re;
}

到这里，模板题就做完了，上代码：

#include

using namespace std;

const int MAXN=100001;

int n,m,l,r,cnt,a[MAXN],minn[MAXN*4];//线段树数组要开大4倍

void build(int now,int l,int r){
	if(l==r){//当l==r时，当前点是叶子节点
		cnt++;
		minn[now]=a[cnt];//minn[now]为当前结点维护的区间的值
		                 //a[cnt]为当前叶子结点的值
	}else{
		int mid=(l+r)/2;
		build(now*2,l,mid);
		build(now*2+1,mid+1,r);
		minn[now]=min(minn[now*2],minn[now*2+1]);
	}
}

int get_min(int now,int l,int r,int q_l,int q_r){//查询[q_l,q_r]的最小值
	int re=0x7fffffff;
	if(q_l<=l&&q_r>=r){//如果查询区间把当前区间覆盖
		re=minn[now];
	}else{
		int mid=(l+r)/2;
		if(q_l<=mid)re=min(re,get_min(now*2,l,mid,q_l,q_r));
		//如果查询区间与左儿子的区间有交集，查询左儿子的区间
		if(q_r>mid)re=min(re,get_min(now*2+1,mid+1,r,q_l,q_r));
		//如果查询区间与右儿子的区间有交集，查询右儿子的区间
	}
	return re;
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	build(1,1,n);
	while(m--){
		scanf("%d%d",&l,&r);
		printf("%d ",get_min(1,1,n,l,r));
	}
}

---

更进一步的学习:

引入

依然是扔一道模板题上来 洛谷P3372
题意大致是：维护一个长度为$n$区间，支持一下两种操作：

1. 把某一个区间的值加上$x$
2. 查询区间和
   如果暴力修改的话，一次修改的时间复杂度是$O(N)$的那么总时间复杂度就是$O(N^2)$的了，理论上是会TLE的，或许会吧，我没试过
   这时候，我们依然可以使用线段树

---

正题

线段树的区间修改:

题目需要我们修改一段区间的值，我们自然需要使用到线段树的区间修改操作
思路其实是和区间查询的思路差不多的，这里有两种打法，其中第二种比第一种优越

1. 不带lazy_tag

这就非常好打了，我们平常不用这种打法，因为常数太大了
上代码

void update(int now,int l,int r,int q_l,int q_r,int x){
	if(l==r)sum[now]=sum[now]+x;else{
		int mid=(l+r)/2;
		if(q_l<=mid)update(now*2,l,mid,p_l,p_r,x);
		if(q_r>mid)update(now*2+1,mid+1,r,p_l,p_r,x);
		sum[now]=sum[now*2]+sum[now*2+1];
	}
}

我们会发现，这样修改的话，会有很多冗余的修改操作,它的效率甚至可能比不上暴力：
比如我们先修改了区间$[2,6]$,再修改区间$[4,8]$的话，$[4,6]$这段区间就被修改了两次
但是如果我们使用lazy_tag,就可以把两次操作变成一次操作

2. 带lazy_tag

lazy_tag的思想是，我们把一个区间拆成多个区间，每个区间打上一个标记，标记它的叶子节点要加上多少，它自己的值可以在$O(1)$的时间内算出，等到我们要使用它的儿子时，再把标记下压到它的儿子上
首先，我们需要一个更新自己的push_up()函数

void push_up(int now){
	sum[now]=sum[now*2]+sum[now*2+1];
}

然后，我们需要一个push_down()函数，用于下压标记

void push_down(int now,int l,int r){
	if(tag[now]){//如果节点带有标记
		int mid=(l+r)/2;
		sum[now*2]=sum[now*2]+(mid-l+1)*tag[now];
		sum[now*2+1]=sum[now*2+1]+(r-mid)*tag[now];
		tag[now*2]=tag[now*2]+tag[now];
		tag[now*2+1]=tag[now*2+1]+tag[now];
		tag[now]=0;
		push_up(now);
	}
}

然后就是我们的修改update()函数

void update(int now,int l,int r,int q_l,int q_r,int x){
	if(q_l<=l&&q_r>=r){
		sum[now]=sum[now]+(r-l+1)*x;
		tag[now]=tag[now]+x;
	}else{
		push_down(now,l,r);
		int mid=(l+r)/2;
		if(q_l<=mid)update(now*2,l,mid,q_l,q_r,x);
		if(q_r>mid)update(now*2+1,mid+1,r,q_l,q_r,x);
		push_up(now);
	}
}

我们还需要一个新的区间查询get_sum()

int get_sum(int now,int l,int r,int q_l,int q_r){
	int re=0;
	if(q_l<=l&&q_r>=r)re=re+sum[now];else{
		push_down(now,l,r);
		int mid=(l+r)/2;
		if(q_l<=mid)re=re+get_sum(now*2,l,mid,q_l,q_r);
		if(q_r>mid)re=re+get_sum(now*2+1,mid+1,q_l,q_r);
		push_up(now);
	}
	return re;
}

于是这题我们就做完了,上代码

#include

using namespace std;

const int MAXN=100001;

int n,m,t,x,y,cnt;

long long sum[MAXN*4],tag[MAXN*4],a[MAXN],z;

void push_up(int now){
	sum[now]=sum[now*2]+sum[now*2+1];
}

void push_down(int now,int l,int r){
	if(tag[now]){//如果节点带有标记
		int mid=(l+r)/2;
		sum[now*2]=sum[now*2]+(mid-l+1)*tag[now];
		sum[now*2+1]=sum[now*2+1]+(r-mid)*tag[now];
		tag[now*2]=tag[now*2]+tag[now];
		tag[now*2+1]=tag[now*2+1]+tag[now];
		tag[now]=0;
		push_up(now);
	}
}

void build(int now,int l,int r){
	if(l==r){cnt++;sum[now]=a[cnt];}else{
		int mid=(l+r)/2;
		build(now*2,l,mid);
		build(now*2+1,mid+1,r);
		push_up(now);
	}
}

void update(int now,int l,int r,int q_l,int q_r,long long x){
	if(q_l<=l&&q_r>=r){
		sum[now]=sum[now]+(r-l+1)*x;
		tag[now]=tag[now]+x;
	}else{
		push_down(now,l,r);
		int mid=(l+r)/2;
		if(q_l<=mid)update(now*2,l,mid,q_l,q_r,x);
		if(q_r>mid)update(now*2+1,mid+1,r,q_l,q_r,x);
		push_up(now);
	}
}

long long get_sum(int now,int l,int r,int q_l,int q_r){
	long long re=0;
	if(q_l<=l&&q_r>=r)re=re+sum[now];else{
		push_down(now,l,r);
		int mid=(l+r)/2;
		if(q_l<=mid)re=re+get_sum(now*2,l,mid,q_l,q_r);
		if(q_r>mid)re=re+get_sum(now*2+1,mid+1,r,q_l,q_r);
		push_up(now);
	}
	return re;
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
	build(1,1,n);
	while(m--){
		scanf("%d",&t);
		if(t==1){
			scanf("%d%d%lld",&x,&y,&z);
			update(1,1,n,x,y,z);
		}else{
			scanf("%d%d",&x,&y);
			printf("%lld\n",get_sum(1,1,n,x,y));
		}
	}
}

---

线段树的实(shen)用(qi)使用方法:

1. [2016常州一中夏令营Day7]序列

【题目描述】
蛤布斯有一个序列，初始为空。它依次将1-n插入序列，其中i插到当前第ai个数的右边 (ai=0表示插到序列最左边)。它希望你帮它求出最终序列。
【输入数据】
第一行一个整数n。第二行n个正整数a1~an。
【输出数据】
输出一行n个整数表示最终序列，数与数之间用一个空格隔开。
【样例输入】
5
0 1 1 0 3
【样例输出】
4 1 3 5 2
【数据范围】
对于30%的数据，n<=1000。
对于70%的数据，n<=100000
对于100%的数据，n<=1000000，0<=ai

题解:
我们容易可以发现一点：后插入的元素会影响到先前插入的元素的位置，所以我们不妨从后向前处理
不难发现，插入的规则可以看成：从后向前处理，每个元素插入到当前从前向后数第$a[i]+1$个空位值上
那么这题的问题就转换为如何找到当前第$a[i]+1$个空格的下标了
因为空格的位置是严格递增的，那么我们考虑使用线段树来维护每个区间有多少空格
然后我们就可以在$O(\log N)$的时间内查询到第$a[i]+1$个空格的下标
这个问题就这样解决了
代码：

#include

using namespace std;

const int MAXN=1000001;

int n,x,tmp,ans[MAXN],sum[MAXN*4],pos[MAXN*4],a[MAXN];

void build(int now,int l,int r){
	if(l==r){
		tmp++;
		pos[now]=tmp;
		sum[now]=1;
	}else{
		int mid=(l+r)>>1;
		build(now*2,l,mid);
		build(now*2+1,mid+1,r);
		sum[now]=sum[now*2]+sum[now*2+1];
	}
}

void update(int now,int l,int r,int x,int y){
	if(l==r){
		sum[now]=sum[now]+y;
	}else{
		int mid=(l+r)>>1;
		if(x<=mid)update(now*2,l,mid,x,y);
		if(x>mid)update(now*2+1,mid+1,r,x,y);
		sum[now]=sum[now*2]+sum[now*2+1];
	}
}

int find(int now,int l,int r,int x){
	if(l==r){
		return pos[now];
	}else{
		int mid=(l+r)>>1,ls=sum[now*2];
		if(x<=ls)return find(now*2,l,mid,x);
		if(x>ls)return find(now*2+1,mid+1,r,x-ls);
	}
}

int main(){
	scanf("%d",&n);
	build(1,1,n);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	for(int i=n;i>=1;i--){
		x=a[i];
		x++;
		int now=find(1,1,n,x);
		update(1,1,n,now,-1);
		ans[now]=i;
	}
	for(int i=1;i<=n;i++)printf("%d ",ans[i]);
}

2. CF558E A Simple Task

题意:维护一个仅含小写字母的字符串，要求支持区间升序、降序排序，并把处理后的字符串输出
题解
我们维护26颗线段树，储存26个字母，每个字母的位置和总数
排序操作就是先对26颗线段树进行区间查询字母个数，并清除，排序后再重新放到线段树里
思想很简单，但是代码细节较多

#include
 
using namespace std;
 
const int MAXN=10000001;
 
int len,m,num_of_node;
char st[1000001];
 
struct segment_tree{
    int root[27],tmp[27],ls[MAXN],rs[MAXN],sum[MAXN],tag_add[MAXN];
    bool tag_cle[MAXN];
    void push_up(int now){
        sum[now]=sum[ls[now]]+sum[rs[now]];
    }
    void push_down(int now,int l,int r){
        int mid=(l+r)>>1,add=tag_add[now];
        bool cle=tag_cle[now];
        tag_add[now]=0;tag_cle[now]=false;
        if(l==r)return;
        if(cle){
            tag_cle[ls[now]]=tag_cle[rs[now]]=true;
            sum[ls[now]]=sum[rs[now]]=tag_add[ls[now]]=tag_add[rs[now]]=0;
        }
        tag_add[ls[now]]=tag_add[ls[now]]+add;
        tag_add[rs[now]]=tag_add[rs[now]]+add;
        sum[ls[now]]=sum[ls[now]]+add*(mid-l+1);
        sum[rs[now]]=sum[rs[now]]+add*(r-mid);
    }
    void build(int now,int l,int r){
        if(l==r)return;
        int mid=(l+r)>>1;
        ls[now]=++num_of_node;
        build(ls[now],l,mid);
        rs[now]=++num_of_node;
        build(rs[now],mid+1,r);
    }
    void update(int now,int l,int r,int ql,int qr){
        if(ql<=l&&qr>=r){
            sum[now]=sum[now]+(r-l+1);
            tag_add[now]++;
        }else{
            push_down(now,l,r);
            int mid=(l+r)>>1;
            if(ql<=mid)update(ls[now],l,mid,ql,qr);
            if(qr>mid)update(rs[now],mid+1,r,ql,qr);
            push_up(now);
        }
    }
    int get_sum_and_clear(int now,int l,int r,int ql,int qr){
        int re=0;
        if(ql<=l&&qr>=r){
            re=sum[now];
            tag_cle[now]=true;
            tag_add[now]=sum[now]=0;
        }else{
            push_down(now,l,r);
            int mid=(l+r)>>1;
            if(ql<=mid)re=get_sum_and_clear(ls[now],l,mid,ql,qr);
            if(qr>mid)re=re+get_sum_and_clear(rs[now],mid+1,r,ql,qr);
            push_up(now);
        }
        return re;
    }
}t;
 
int main(){
    scanf("%d%d",&len,&m);
    scanf("%s",st+1);
    for(int i=1;i<=26;i++){
        t.root[i]=++num_of_node;
        t.build(t.root[i],1,len);
    }
    for(int i=1;i<=len;i++){
        t.update(t.root[st[i]-'a'+1],1,len,i,i);
    }
    for(int i=1;i<=m;i++){
        int l,r,mode;
        scanf("%d%d%d",&l,&r,&mode);
        for(int j=1;j<=26;j++)t.tmp[j]=t.get_sum_and_clear(t.root[j],1,len,l,r);
        if(mode){
            int now=l;
            for(int j=1;j<=26;j++)if(t.tmp[j]){
                t.update(t.root[j],1,len,now,now+t.tmp[j]-1);
                now=now+t.tmp[j];
            }
        }else{
            int now=r;
            for(int j=1;j<=26;j++)if(t.tmp[j]){
                t.update(t.root[j],1,len,now-t.tmp[j]+1,now);
                now=now-t.tmp[j];
            }
        }
    }
    for(int i=1;i<=len;i++){
        for(int j=1;j<=26;j++){
            if(t.get_sum_and_clear(t.root[j],1,len,i,i)){
                printf("%c",j+'a'-1);
                break;
            }
        }
    }
}

---

3. CF787D Legacy（线段树优化建图）

题意:
你有$n$个点和$m$个操作，操作分三种类型:

1. 从$v$到$u$连一条长度为$w$的有向边
2. 从$v$到$l\sim r$每一个点连一条长度为$w$的有向边
3. 从$l\sim r$到$u$每一个点连一条长度为$w$的有向边
   求$m$次操作后节点$s$到每一个点的最短路径
   题解:
   建完图后直接跑最短路，问题在于建图
   如果暴力建图，肯定是$O(N^2)$的，会TLE
   考虑到它是区间向点连边，我们就可以用线段树优化建图
   建两颗线段树，一颗原树，一颗汇树
   原树连边方向从叶子节点联想父亲结节点，汇树连边方向相反
   先把原树和汇树的对应的叶子节点连双向边，再处理每一个操作
   操作二就是从原树的一个点向汇树的区间连边，连边方法就是把区间拆开
   比如我们原来要从$1$到$4\sim 8$连边，原来要连四条，现在只用连一条即可
   操作三就是从原树上的区间向汇树上的点连边
   建图的时间复杂度就被我们优化到了$O(N\log N)$
   然后再跑最短路算法即可

#include
 
using namespace std;
 
const int MAXN=1000001,MAXM=7000001;
 
struct edge{
    int from,to,nxt;
    long long len;
    edge(int from_=0,int to_=0,long long len_=0,int nxt_=0){from=from_;to=to_;len=len_;nxt=nxt_;}
}e[MAXM];
 
int n,m,s,t,start,tmp,num_of_node,num_of_edge,from,from_l,from_r,to,to_l,to_r,ch[MAXN][2],head[MAXN],g[100001][2];
long long dis[MAXN],z;
bool in[MAXN];
 
void add_edge(int from,int to,int len){
    num_of_edge++;
    e[num_of_edge]=edge(from,to,len,head[from]);
    head[from]=num_of_edge;
}
 
void build_from(int now,int l,int r){
    if(l==r){tmp++;if(tmp==s)start=now;g[tmp][0]=now;return;}
    int mid=(l+r)>>1;
    num_of_node++;
    ch[now][0]=num_of_node;
    add_edge(ch[now][0],now,0);
    build_from(ch[now][0],l,mid);
    num_of_node++;
    ch[now][1]=num_of_node;
    add_edge(ch[now][1],now,0);
    build_from(ch[now][1],mid+1,r);
}
 
void build_to(int now,int l,int r){
    if(l==r){tmp++;g[tmp][1]=now;return;}
    int mid=(l+r)>>1;
    num_of_node++;
    ch[now][0]=num_of_node;
    add_edge(now,ch[now][0],0);
    build_to(ch[now][0],l,mid);
    num_of_node++;
    ch[now][1]=num_of_node;
    add_edge(now,ch[now][1],0);
    build_to(ch[now][1],mid+1,r);
}
 
void add_from(int now,int l,int r,int ql,int qr,int link,long long len){
    if(ql<=l&&qr>=r){
        add_edge(now,link,len);
    }else{
        int mid=(l+r)>>1;
        if(ql<=mid)add_from(ch[now][0],l,mid,ql,qr,link,len);
        if(qr>mid)add_from(ch[now][1],mid+1,r,ql,qr,link,len);
    }
}
 
void add_to(int now,int l,int r,int ql,int qr,int link,long long len){
    if(ql<=l&&qr>=r){
        add_edge(link,now,len);
    }else{
        int mid=(l+r)>>1;
        if(ql<=mid)add_to(ch[now][0],l,mid,ql,qr,link,len);
        if(qr>mid)add_to(ch[now][1],mid+1,r,ql,qr,link,len);
    }
}
 
void build_graph(int l_1,int r_1,int l_2,int r_2,long long len){
    int link=++num_of_node;
    add_from(1,1,n,l_1,r_1,link,len);
    add_to(2,1,n,l_2,r_2,link,0);
}
 
void build_graph_i_to_i(int i){
    add_edge(g[i][0],g[i][1],0);
    add_edge(g[i][1],g[i][0],0);
}
 
void SPFA(int start){
    memset(dis,-1,sizeof(dis));
    queue<int>q;
    q.push(start);
    dis[start]=0;in[start]=true;
    while(!q.empty()){
        int now=q.front();q.pop();in[now]=false;
        for(int i=head[now];~i;i=e[i].nxt){
            int to=e[i].to;
            if(dis[to]>dis[now]+e[i].len||dis[to]==-1){
                dis[to]=dis[now]+e[i].len;
                if(!in[to])q.push(to);
                in[to]=true;
            }
        }
    }
}
 
void dfs(int now,int l,int r){
    if(l==r){printf("%lld ",dis[now]);return;}else{
        int mid=(l+r)>>1;
        dfs(ch[now][0],l,mid);
        dfs(ch[now][1],mid+1,r);
    }
}
 
int main(){
    memset(head,-1,sizeof(head));
    scanf("%d%d%d",&n,&m,&s);
    num_of_node=2;
    tmp=0;build_from(1,1,n);tmp=0;build_to(2,1,n);
    for(int i=1;i<=n;i++)build_graph_i_to_i(i);
    for(int i=1;i<=m;i++){
        scanf("%d",&t);
        if(t==1){
            scanf("%d%d%lld",&from,&to,&z);
            build_graph(from,from,to,to,z);
        }else if(t==2){
            scanf("%d%d%d%lld",&from,&to_l,&to_r,&z);
            build_graph(from,from,to_l,to_r,z);
        }else if(t==3){
            scanf("%d%d%d%lld",&to,&from_l,&from_r,&z);
            build_graph(from_l,from_r,to,to,z);
        }
    }
    SPFA(start);
    dfs(2,1,n);
}