TensorFlow之线性回归

       通过tensorflow实现一个简易的线性回归，代码如下：

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

#定义训练数据
train_x = np.linspace(-1,1,100)
train_y = 3*train_x + np.random.randn(*train_x.shape)*0.33 + 10

#定义输入输出
x = tf.placeholder(dtype=tf.float32)
y_ = tf.placeholder(dtype=tf.float32)

#定义权值和偏置
w = tf.Variable(0.0,name="weight")
b = tf.Variable(0.0,name="bias")

#定义预测输出
y = w*x + b

#定义损失函数和反向传播算法
loss = tf.square(y-y_)
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(loss)

#创建会话
with tf.Session() as sess:
    sess.run(tf.initialize_all_variables())
    
    for i in range(10):
        for (X,Y) in zip(train_x,train_y):
            _,w_value,b_value = sess.run([train_step,w,b],feed_dict={x:X,y_:Y})
        print("step:{},w:{},b:{}".format(i+1,w_value,b_value))
        #绘图
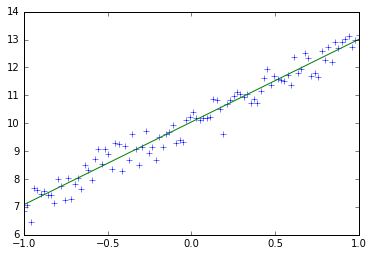
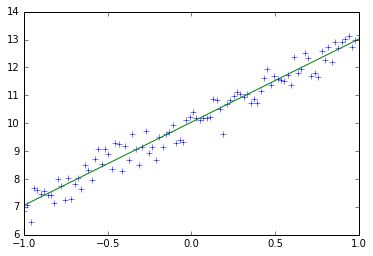
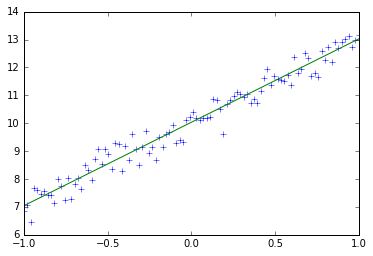
        plt.plot(train_x,train_y,'+')
        plt.plot(train_x,w.eval()*train_x+b.eval())
        plt.show()

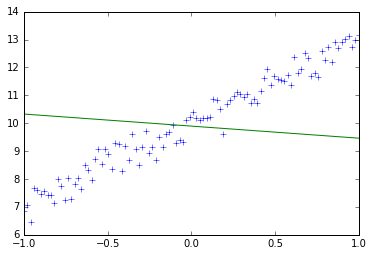
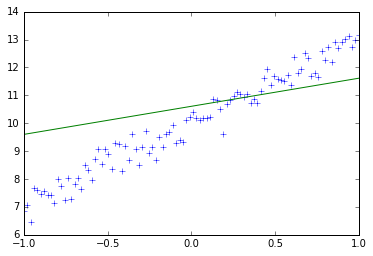
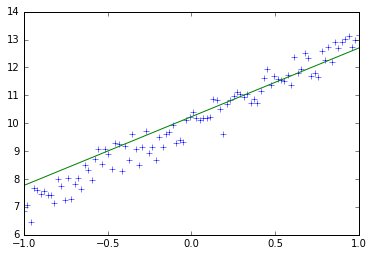
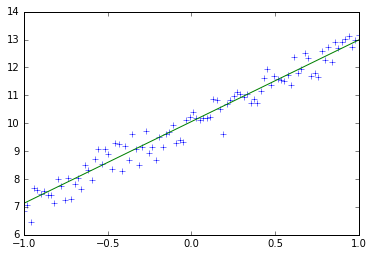
       训练10次后，w接近为3，b接近为10，这和上述代码定义训练数据中的train_y的定义十分接近，10次迭代训练的每一次权值和偏置变化以及图形变化如下所示：

       step:1,w:-0.4323926568031311,b:9.895733833312988

       step:2,w:1.006221890449524,b:10.605839729309082

       step:3,w:1.9528942108154297,b:10.40628719329834

       step:4,w:2.4621810913085938,b:10.232091903686523

       step:5,w:2.7247731685638428,b:10.134077072143555

       step:6,w:2.8587703704833984,b:10.083012580871582

       step:7,w:2.926967144012451,b:10.056891441345215

       step:8,w:2.961653470993042,b:10.043588638305664

       step:9,w:2.9792935848236084,b:10.036816596984863

       step:10,w:2.9882631301879883,b:10.03337574005127