吴恩达机器学习系列理论加实践(五/六 、逻辑回归及matlab实践)
五、Octave教程
这一块课程介绍的是关于Octave软件使用相关的知识,我这里使用的是matlab,所以对于这一块也没有具体跟进,有兴趣的可以自我学习。
**
第三周
**
六、逻辑回归
6.1分类问题
之前课程介绍的是线性回归问题(连续值),现在开始学习逻辑回归分类问题(离散值)。
分类问题的例子有:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否是欺诈;区别一个肿瘤是恶性的还是良性的。

现在讨论二分类问题:是不是恶性肿瘤,如下所示,是则为1,不是则为0;取阈值0.5,对于预测值大于等于0.5的则预测为1,否则预测为0(注意逻辑回归的取值范围为0-1):

6.2模型h表示
根据上面我们知道首先模型h要满足其最终取值位于0-1之间,而线性回归算法其取值显然是不满足的,所以我们引入逻辑回归模型。
最常用的逻辑回归模型为S形函数(sigmoid function:g(z)):
![]()


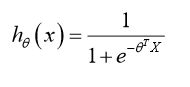
在原来的模型theta*X的基础上加上了一个激活函数g(z),使其取值范围缩放到了0-1,在这里h(x)的值表示的意思是:对于当前变量X在已有参数theta下预测为正例即y=1的概率是多少。
6.3决策边界
决策边界简单点说就是将正负样本分开的边界。

当g(z)>=0.5时,预测为y=1,也即z=thetaX>=0时;
假设theta=[-3 1 1],对于如下式子,thetaX=0时,可以得到决策边界x1+x2=3:
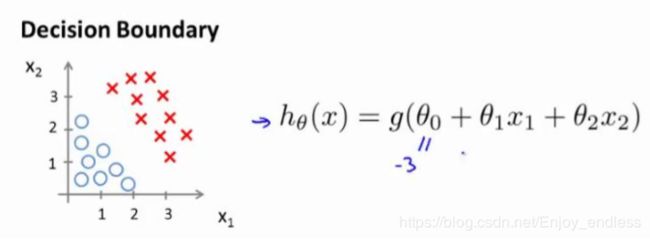
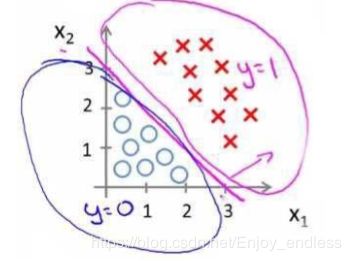
而对于如下分布案例,我们可以利用高次方程拟合曲线,来作为最终的决策边界:

6.4代价函数
在线性回归当中,我们定义的代价函数是误差平方和的形式,在这里如果我们利用相同的形式,那么得到的代价函数与参数的关系将是非凸函数(因为模型h值与参数theta之间加入了激活函数sigmoid,将不再是线性关系):
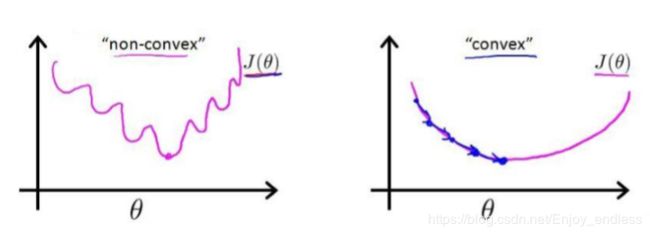
如上图非凸意味着函数将会有很多局部极小值,这将会影响梯度下降法寻找全局最小值,所以之前的代价函数不可用了。
于是我们重新定义代价函数:
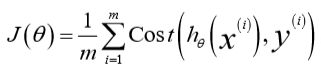

从直观上来理解这个代价函数的正确性:如上图所示横轴表示模型预测值h(x),而纵轴表示代价。当我们的真实标签为y=1时,h(x)的值在0-1之间变化时可以看到他的代价函数是从无穷到0的(左上图);相反右上图同理;这是符合我们想要的结果的:即若真实y=1,而预测h(x)=0则代价将非常高,当我们的预测结果逐步逼近1时其代价将是快速下降直到0。
当然这只是直观上说这个代价函数是符合预期效果的,但它却不是凭空拍脑袋出来的,关于他的具体推导由来在我之前博客《机器学习算法系列》也有过讲解,这正是本课程特点:简单、易懂,从直觉上出发,并不是非常注重原理上的推导。
将如上代价函数整合一下,并带入到代价函数我们可以得到:

6.5梯度下降
有了上面的代价函数,那么我们的目标就是最小化代价函数,然后求得参数theta;我们将其求导带入梯度下降算法可以得到:

可以看到如上梯度更新形式跟线性规划的梯度更新形式是一样的,但是注意这里的模型h(x)与之前的计算是不同的(加入了激活函数)。
另一个需要注意的是在之前我们讲了特征缩放的方法可以加快收敛,在这里同样的特征缩放也是非常有必要的。
6.6高级优化
之前我们讲解学习的优化算法一直是梯度下降法,其实还有一些其他算法,更高级、更复杂,但是速度会更快一些。比如共轭梯度法BFGS和L-BFGS等,它们需要有一种方法来计算 代价J(theta),以及需要一种方法计算导数项,然后使用比梯度下降更复杂的算法来最小化代价函数。这些算法的具体细节超出了本门课程的范畴。
但是他们拥有许多优点:一个是使用这其中任何一个算法,你通常不需要手动选择学习率 α,所以对于这些算法的一种思路是,给出计算导数项和代价函数的方法,你可以认为算法有一个智能的内部循环,而且,事实上,他们确实有一个智能的内部循环,称为线性搜索(line search)算法,它可以自动尝试不同的学习速率 α,并自动选择一个好的学习速率 α,因此它甚至可以为每次迭代选择不同的学习速率,那么你就不需要自己选择。这些算法实际上在做更复杂的事情,而不仅仅是选择一个好的学习率,所以它们往往最终收敛得远远快于梯度下降。
我们实际上完全有可能成功使用这些算法,并应用于许多不同的学习问题,而不需要真正理解这些算法的内环间在做什么,如果说这些算法有缺点的话,那么我想说主要缺点是它们比梯度下降法复杂多了,特别是你最好不要使用 L-BGFS、 BFGS 这些算法,除非你是数值计算方面的专家。实际上,我不会建议你们编写自己的代码来计算数据的平方根,或者计算逆矩阵,因为对于这些算法,我还是会建议你直接使用一个软件库,比如说,要求一个平方根,我们所能做的就是调用一些别人已经写好用来计算数字平方根的函数。幸运的是现在我们有 Octave 和与它密切相关的 MATLAB 语言可以使用。
Octave 有一个非常理想的库用于实现这些先进的优化算法,所以,如果你直接调用它自带的库,你就能得到不错的结果。我必须指出这些算法实现得好或不好是有区别的,因此如果你正在你的机器学习程序中使用一种不同的语言,比如如果你正在使用 C、C + + 、Java等等,你可能会想尝试一些不同的库,以确保你找到一个能很好实现这些算法的库。因为在 L-BFGS 或者等高线梯度的实现上,表现得好与不太好是有差别的。
这些算法的运行速度通常远远超过梯度下降。 所以当我有一个很大的机器学习问题时,我会选择这些高级算法,而不是梯度下降。有了这些概念,你就应该能将逻辑回归和线性回归应用于更大的问题中,这就是高级优化的概念。
这一节主要是介绍了比梯度下降法更高级的一些优化算法,他们执行起来更加快速但是操作调试起来去是非常繁琐复杂,我们没有必要去弄明白他真正的运行原理是什么,我们只需要知道如何利用语言、软件去调用执行他就可以了。所以主要是介绍了相关函数的使用,在下面的matlab代码中我们将会涉及到相关知识。
6.7多分类:一对多
上面讲解的是二分类问题,现在我们还看一下多分类问题。
实例:
1、邮件分类:将收到的文件可以自动归纳到不同的类别,如来自工作的、朋友的、有关兴趣爱好的还是垃圾邮件等等,可以分别用类别y=1,y=2,y=3等等;
2、病人鼻塞病情诊断:y=1过敏,y=2感冒,y=3发烧等等;
3、区分天气情况:晴、多云、阴、雨等等;

如上个图假如有三类,我们用不同形状、颜色进行表示;
对于二分类问题我们可以利用逻辑回归中间用直线或者曲线进行分离,在这里多分类,我们同样可以利用此思想,将其转化为多个二分类任务:比如这里一共三类我们可以转化为三个二分类任务;
比如分别从从类别1三角形开始,将另外两类看作一类,以此类推,如下图所示我们可以拟合出三个分类模型:
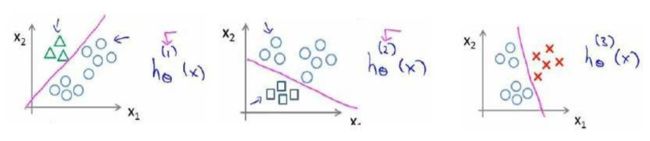
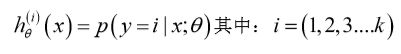
对于我们需要测试的值,分别输入到每个模型分别得到一个值,最后我们取最大的一个就可以了;这就是多类别分类问题,以及一对多的方法,通过这个小方法,你现在也可以将逻辑回归分类器用在多类分类的问题上。
%matlab代码实践
%加载数据
data=load('ex2data1.txt');
X=data(:,1:2);y=data(:,3);
%二维展示数据,X第一列为横坐标,第二列为纵坐标,y表示正负类别
pos=find(y==1); neg=find(y==0);
%正例,红色+号显示,线宽2大小4
plot(X(pos,1),X(pos,2),'r+','LineWidth',2,'MarkerSize',4);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'm', 'MarkerSize', 4);
xlabel('Exam 1 score'); %坐标表示
ylabel('Exam 2 score');
legend('Admitted','Not admitted'); %类别标识
%激活函数sigmoid实现
function g=sigmoid(z)
g=zeros(size(z))
z=1./(1+exp(-z));
%损失函数及梯度计算
function [J,grad]=costFunction(theta,X,y)
m=length(y);
J=0;
grad=zeros(size(theta));
h=sigmoid(X*theta);
J=(-y'*log(h)-(1-y)'*log(1-h))/m;
grad=X'*(h-y)/m;
%调用更优的内置优化函数
%不需要我们手动设置学习速率α,而是通过封装的算法自动计算α进行梯度下降,这将大大提
%高速率,加快收敛。函数不停迭代直到终止条件出现,停止运算,然后输出结果。
options=optimset('GradObj','on','MaxIter',400); %参数GradObj设置为on表示使用自定义的梯度法即上面定义的costFunction的返回值
[theta,cost]=fminunc(@(t)(costFunction(t,X,y)),initial_theta,options);
%预测
prob=sigmoid([1 45 85]*thetha);%单个案例测试
fprintf('%f\n',prob);
function p=predict(theta,X)%测试所有案例
m=length(y);
p=zeros(m,1);
p=sigmoid(theta*X)>=0.5;
fprintf('%f\n',mean(double(p==y))*100);
这一讲主要介绍了逻辑回归的基本概念、知识,包括单/多分类、模型假设、损失函数、更快速的内置优化函数等等;
下一讲 七、正则化