MATLAB实现图像巴特沃斯滤波、高频增强滤波及直方图均衡化
1、巴特沃斯滤波器
1.1 基本概念
在图像处理中,巴特沃斯滤波器传递函数如下:
巴特沃斯低通滤波器公式:
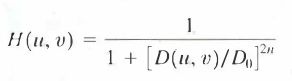
巴特沃斯高通滤波器公式:
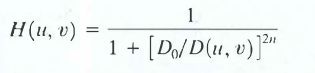
在公式中,D(u,v)代表频域当中,点(u,v)到中心点的距离,我们知道二维图像的傅里叶变换的频域幅值图大概是长这样的:
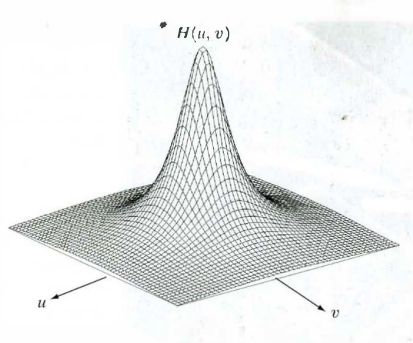
所以中心点也就是(M/2,N/2),M和N代表图像的长和宽,那么D(u,v)就可以用下面的式子来表示了:
![]()
而D0就是截止距离了,就相当于在频域当中画一个圈,对圈内或者圈外保留就可以达到所谓的低通和高通了,这个D0就相当于一维当中的截止频率。
1.2 MATLAB实现
有了上面的概念理解,程序实现起来也不难了。基本的思路就是先对图像进行二维傅里叶变换,之后根据公式设计巴特沃斯滤波器的传递函数,在频域对图像进行处理,最后再傅里叶反变换回来就结束了。具体代码如下:
clear all;
clc;
%% 读取原图像
Original_image=imread('Origin.tif');
[len,wid]=size(Original_image);
Original_image=im2double(Original_image);
g=fft2(Original_image); %二维傅立叶变换
g=fftshift(g); %频移
%% 设计巴特沃斯滤波器
n1=2; %巴特沃斯滤波器阶数为2
D0=0.05*len; %截止频率5%的图像宽度
[M,N]=size(g);
m=fix(M/2);
n=fix(N/2);
for i=1:M
for j=1:N
D=sqrt((i-m)^2+(j-n)^2);
h1=1/(1+(D0/D)^(2*n1)); %计算高通滤波器传递函数
h2=0.5+2*h1; %设计high-frequency emphasis其中a=0.5,b=2.0
s1(i,j)=h1*g(i,j); %用设计的滤波器处理原图像
end
end
%% 傅里叶反变换后
filter_image1=im2uint8(real(ifft2(ifftshift(s1)))); %傅里叶反变换
%% 变换前后图像显示
subplot(1211),imshow(Original_image),title('(a) A chest X-ray image');
subplot(122),imshow(filter_image1),title('(b) Result of Butterworth highpass filtering');
1.3 处理结果
2、高频增强滤波器(High-Frequency Emphasis Filtering)
2.1 基本概念
高频增强滤波器的传递函数如下:
![]()
其中a>=0,b>a,Hhp(u,v)表示高通滤波器,这个滤波器在保留高频分量的同时,也加入了背景的低频成分。
2.2 Matlab实现
这个也比较简单,只要在上面的
h1=1/(1+(D0/D)^(2*n1)); %计算高通滤波器传递函数
这句代码的后面添加一句就行了:
h2=0.5+2*h1; %设计high-frequency emphasis其中a=0.5,b=2.0
s2(i,j)=h2*g(i,j); %用设计的high-frequency emphasis滤波器处理原图像
之后同样是反变换一下得到变换后的图像:
filter_image2=im2uint8(real(ifft2(ifftshift(s2)))); %傅里叶反变换
subplot(121),imshow(Original_image),title('(a) A chest X-ray image');
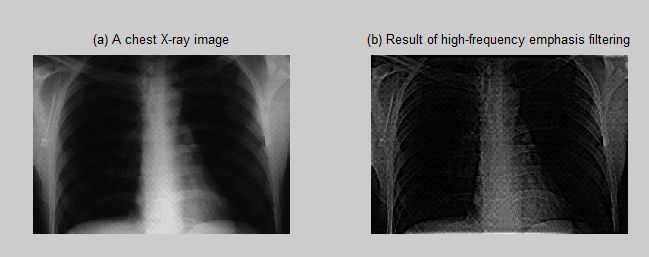
subplot(122),imshow(filter_image2),title('(b) Result of high-frequency emphasis filtering');
2.3 处理结果
3、直方图均衡化
3.1 基本概念
直方图均值通俗来说就是把一幅图像的灰度值集合,通过一定的映射关系,映射到另一个灰度值集合中,其目的就是为了使各个灰度级点数比较均衡同时达到增强对比度的效果,具体怎么做我也不介绍了,网上的资料也比较多。这里贴一篇——直方图均衡化
3.2 MATLAB实现
直方图均衡化MATLAB中其实是有封装好的函数的即histeq()函数:
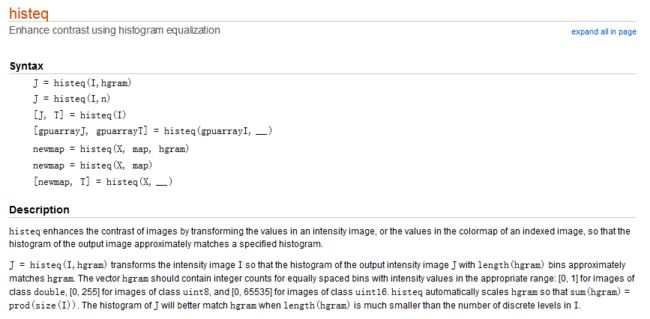
另外还有一个显示图像直方图分布的函数——imhist()函数
但是在这里为了看一下直方图均衡化到底是怎么实现的,我还是自己码一下,这样可以了解一下实现过程,更熟悉掌握。
3.2.1 直方图均值化——自己编写代码
直接按照均衡化的思路来码代码,基本是以下几个步骤:
1.统计各像素点的灰度值
2.各灰度级的概率计算
3.累积概率分布函数计算
4.灰度级映射
直接看代码,我们这个是在第2部分高通增强基础filter_image2上进行的:
%% 直方图均衡化
%进行像素灰度统计;
s = zeros(1,256);%统计各灰度数目,共256个灰度级
for i = 1:len
for j = 1: wid
s(filter_image2(i,j) + 1) = s( filter_image2(i,j) + 1) + 1;%对应灰度值像素点数量增加一
end
end
%计算灰度分布密度
p = zeros(1,256);
for i = 1:256
p(i) = s(i) / (len * wid * 1.0);
end
%计算累计直方图分布
c = zeros(1,256);
c(1) = p(1);
for i = 2:256
c(i) = c(i - 1) + p(i);
end
%累计分布取整,将其数值归一化为1~256
c = uint8(255 .* c + 0.5);
%对图像进行均衡化
for i = 1:len
for j = 1: wid
hist_image(i,j) = c(filter_image2(i,j)+1);
end
end
3.2.2 直方图均衡化——MATLAB自带函数
这就更简单了,如下:
mat_hist_image=histeq(filter_image2,256);
3.3 处理结果
最后我们来看看自己码的直方图均衡化代码和MATLAB自带的函数处理的结果:
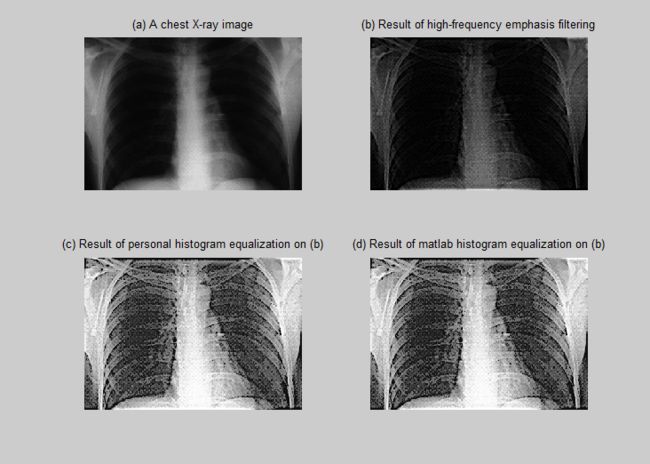
图©和图(d)分别表示两种处理的结果,看到效果基本是一样的,与图(b)比较,可以发现背景变得更加清晰了,我们的目的也达到了。
#声明
本文章的公式以及图片来源于冈萨雷斯的《数字图像处理 第2版》Example 4.9