密度聚类之DBSCAN及Python实现

密度聚类

密度聚类，即基于密度的聚类(density-based clustering)，此类算法假设聚类结构能通过样本分布的紧密程度确定。前面所讲的原型聚类及层次聚类等都是把距离(欧式距离，闵科夫斯基距离，曼哈顿距离等)作为两个样本或者两个簇之间相似度的评价指标，因此导致了最终聚类结构大都是球状簇或者凸形集合，对任意形状的聚类簇比较吃力，同时对噪声数据不敏感，而基于密度的聚类算法可以发现任意形状的聚类，且对带有噪音点的数据起着重要的作用。

DBSCAN

DBSCAN(Density-Based Spatial Clustering of Application with Noise)是一种典型的基于密度的聚类算法，能够将足够高密度的区域划分成簇，并能在具有噪声的空间数据库中发现任意形状的簇。它是基于一组“邻域”(neighborhood)参数 (ϵ,MinPts) ( ϵ , M i n P t s ) 来刻画样本分布的紧密程度。

概念

给定数据集 D={x1,x2,...,xm} D = { x 1 , x 2 , . . . , x m } ，定义下面这几个概念：

• ϵ ϵ -邻域：对 xj∈D x j ∈ D ，其 ϵ ϵ -邻域包含样本集 D D 中与 xj x j 的距离不大于 ϵ ϵ 的样本，即 Nϵ(xj)={xi∈D|dist(xi,xj)≤ϵ} N ϵ ( x j ) = { x i ∈ D | d i s t ( x i , x j ) ≤ ϵ } ，这个子样本集的个数记为 |Nϵ(xj)| | N ϵ ( x j ) | ;
• 核心对象(core object):若 xj x j 的 ϵ ϵ -领域至少包含 MinPts M i n P t s 个样本，即 |Nϵ(xj)|≥MinPts | N ϵ ( x j ) | ≥ M i n P t s ，则 xj x j 是一个核心对象；
• 密度直达(directly density-reachable):若 xj x j 位于 xi x i 的 ϵ ϵ -领域中，且 xi x i 是核心对象，则称 xj由xi x j 由 x i 密度直达；注意反之不一定成立，即此时不能说 xi x i 由 xj x j 密度直达，除非 xj x j 也是核心对象；
• 密度可达(density-reachable):对 xi x i 与 xj x j ，若存在样本序列 p1,p2,...,pn p 1 , p 2 , . . . , p n ，其中 p1=xi，pn=xj p 1 = x i ， p n = x j 且 pi+1 p i + 1 由 pi p i 密度直达，则称 xj x j 由 xi x i 密度可达；此时序列中的传递样本 p1,p2,...,pn p 1 , p 2 , . . . , p n 均为核心对象，因为只有核心对象才能使其他样本密度直达，注意密度可达也不满足对称性，这个可以由密度直达的不对称性得出。
• 密度相连(density-connected):对 xi x i 与 xj x j ，若存在 xk x k 使得 xi x i 与 xj x j 均由 xk x k 密度可达，则称 xi x i 与 xj x j 密度相连；注意密度相连关系是满足对称性的。

例子

从下图可以很容易看出理解上述定义，图中 MinPts=5 M i n P t s = 5 ，红色的点都是核心对象，因为其 ϵ ϵ -邻域至少有5个样本。黑色的样本是非核心对象。所有核心对象密度直达的样本在以红色核心对象为中心的超球体内，如果不在超球体内，则不能密度直达。图中用绿色箭头连起来的核心对象组成了密度可达的样本序列。在这些密度可达的样本序列的ϵ-邻域内所有的样本相互都是密度相连的。

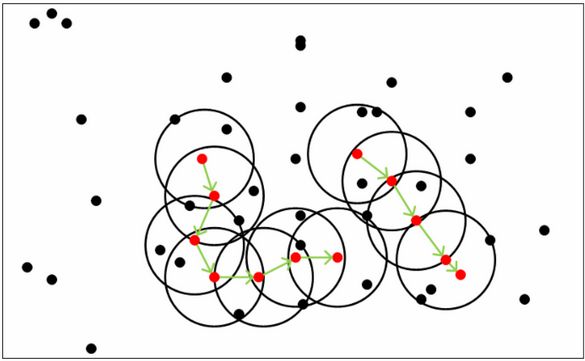
DBSCAN思想

DBSCAN的聚类定义很简单：由密度可达关系导出的最大密度相连的样本集合，即为我们最终聚类的一个类别，或者说一个簇。

这个DBSCAN的簇里面可以有一个或者多个核心对象。如果只有一个核心对象，则簇里其他的非核心对象样本都在这个核心对象的 ϵ ϵ -邻域里；如果有多个核心对象，则簇里的任意一个核心对象的ϵ-邻域中一定有一个其他的核心对象，否则这两个核心对象无法密度可达。这些核心对象的 ϵ ϵ -邻域里所有的样本的集合组成的一个DBSCAN聚类簇。

那么怎么才能找到这样的簇样本集合呢？DBSCAN使用的方法很简单，它任意选择一个没有类别的核心对象作为种子，然后找到所有这个核心对象能够密度可达的样本集合，即为一个聚类簇。接着继续选择另一个没有类别的核心对象去寻找密度可达的样本集合，这样就得到另一个聚类簇。一直运行到所有核心对象都有类别为止。

基本上这就是DBSCAN算法的主要内容了，是不是很简单？但是我们还是有三个问题没有考虑。

• 第一个是一些异常样本点或者说少量游离于簇外的样本点，这些点不在任何一个核心对象在周围，在DBSCAN中，我们一般将这些样本点标记为噪音点。
• 第二个是距离的度量问题，即如何计算某样本和核心对象样本的距离。在DBSCAN中，一般采用最近邻思想，采用某一种距离度量来衡量样本距离，比如欧式距离。这和KNN分类算法的最近邻思想完全相同。对应少量的样本，寻找最近邻可以直接去计算所有样本的距离，如果样本量较大，则一般采用KD树或者球树来快速的搜索最近邻。如果大家对于最近邻的思想，距离度量，KD树和球树不熟悉，建议参考之前刘建平写的另一篇文章K近邻法(KNN)原理小结。
• 第三个问题比较特殊，某些样本可能到两个核心对象的距离都小于 ϵ ϵ ，但是这两个核心对象由于不是密度直达，又不属于同一个聚类簇，那么如果界定这个样本的类别呢？一般来说，此时DBSCAN采用先来后到，先进行聚类的类别簇会标记这个样本为它的类别。也就是说BDSCAN的算法不是完全稳定的算法。

DBSCAN算法流程

这部分主要参考周志华的《机器学习》。

---

输入：样本集 D={x1,x2,...,xm} D = { x 1 , x 2 , . . . , x m } ，领域参数 (ϵ,MinPts) ( ϵ , M i n P t s )
过程：

1. 初始化核心对象集合： Ω=∅ Ω = ∅
2. 对于 j=1,2,...m j = 1 , 2 , . . . m , 按下面的步骤找出所有的核心对象：
   a).根据距离度量公式，确定样本 xj x j 的 ϵ ϵ -邻域 Nϵ(xj) N ϵ ( x j )
   b).if |Nϵ(xj)|≥MinPts | N ϵ ( x j ) | ≥ M i n P t s then
     将样本 xj x j 加入核心对象集合： Ω=Ω⋃{xj} Ω = Ω ⋃ { x j }
    end if
3. 初始化聚类簇数： k=0 k = 0
4. 初始化未访问样本集合： Γ=D Γ = D
5. while Ω≠∅ Ω ≠ ∅ do
    记录当前未访问样本集合： Γold=Γ Γ o l d = Γ ；
    随机选取一个核心对象 o∈Ω o ∈ Ω ，初始化队列 Q=<o> Q =< o >
    while Q≠∅ Q ≠ ∅ do
     取出队列 Q Q 中首个样本 q q ;
     if |Nϵ(xj)|≥MinPts | N ϵ ( x j ) | ≥ M i n P t s then
       令 Δ=Nϵ(q)⋂Γ Δ = N ϵ ( q ) ⋂ Γ ;
       将 Δ Δ 中的样本加入队列 Q Q ;
        Γ=Γ−Δ Γ = Γ − Δ ;
     end if
    end while
   k=k+1 k = k + 1 ,生成聚类簇 Ck=Γold−Γ C k = Γ o l d − Γ
   Ω=Ω−Ck Ω = Ω − C k
   end while

输出：簇划分 C={C1,C2,..,Ck} C = { C 1 , C 2 , . . , C k }

---

python实现

#计算两个向量之间的欧式距离
def calDist(X1 , X2 ):
    sum = 0
    for x1 , x2 in zip(X1 , X2):
        sum += (x1 - x2) ** 2
    return sum ** 0.5

#获取一个点的ε-邻域（记录的是索引）
def getNeibor(data , dataSet , e):
    res = []
    for i in range(shape(dataSet)[0]):
        if calDist(data , dataSet[i])return res

#密度聚类算法
def DBSCAN(dataSet , e , minPts):
    coreObjs = {}#初始化核心对象集合
    C = {}
    n = shape(dataSet)[0]
    #找出所有核心对象，key是核心对象的index，value是ε-邻域中对象的index
    for i in range(n):
        neibor = getNeibor(dataSet[i] , dataSet , e)
        if len(neibor)>=minPts:
            coreObjs[i] = neibor
    oldCoreObjs = coreObjs.copy()
    k = 0#初始化聚类簇数
    notAccess = list(range(n))#初始化未访问样本集合（索引）
    while len(coreObjs)>0:
        OldNotAccess = []
        OldNotAccess.extend(notAccess)
        cores = coreObjs.keys()
        #随机选取一个核心对象
        randNum = random.randint(0,len(cores))
        cores=list(cores)
        core = cores[randNum]
        queue = []
        queue.append(core)
        notAccess.remove(core)
        while len(queue)>0:
            q = queue[0]
            del queue[0]
            if q in oldCoreObjs.keys() :
                delte = [val for val in oldCoreObjs[q] if val in notAccess]#Δ = N(q)∩Γ
                queue.extend(delte)#将Δ中的样本加入队列Q
                notAccess = [val for val in notAccess if val not in delte]#Γ = Γ\Δ
        k += 1
        C[k] = [val for val in OldNotAccess if val not in notAccess]
        for x in C[k]:
            if x in coreObjs.keys():
                del coreObjs[x]
    return C

使用scikit-learn实现

在scikit-learn中，DBSCAN算法类为sklearn.cluster.DBSCAN。

from sklearn.cluster import DBSCAN
#eps为距离阈值ϵ，min_samples为邻域样本数阈值MinPts,X为数据
y_pred = DBSCAN(eps = 0.1, min_samples = 10).fit_predict(X)

DBSCAN算法优缺点

• 优点：可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。可以在聚类的同时发现异常点，对数据集中的异常点不敏感。聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。
• 缺点：如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。如果大家对于最近邻的思想，距离度量，KD树和球树不熟悉，建议参考之前刘建平写的另一篇文章K近邻法(KNN)原理小结。调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值 ϵ ϵ ，邻域样本数阈值 MinPts M i n P t s 联合调参，不同的参数组合对最后的聚类效果有较大影响。

python实例（一）

完整代码请见Github

数据集

数据集是周志华《机器学习》中的西瓜数据集4.0

0.697,0.46
0.774,0.376
0.634,0.264
0.608,0.318
0.556,0.215
0.403,0.237
0.481,0.149
0.437,0.211
0.666,0.091
0.243,0.267
0.245,0.057
0.343,0.099
0.639,0.161
0.657,0.198
0.36,0.37
0.593,0.042
0.719,0.103
0.359,0.188
0.339,0.241
0.282,0.257
0.748,0.232
0.714,0.346
0.483,0.312
0.478,0.437
0.525,0.369
0.751,0.489
0.532,0.472
0.473,0.376
0.725,0.445
0.446,0.459

数据处理

预处理数据

def loadDataSet(filename):
    dataSet = []
    fr = open(filename)
    for line in fr.readlines():
        curLine = line.strip().split(',')
        fltLine = map(float, curLine)
        #python2.x map函数返回list
        #dataSet.append(fltLine)
        #python3.x map函数返回迭代器
        dataSet.append(list(fltLine))
    return dataSet

画图方法

def draw(C , dataSet):
    color = ['r', 'y', 'g', 'b', 'c', 'k', 'm']
    for i in C.keys():
        X = []
        Y = []
        datas = C[i]
        for j in range(len(datas)):
            X.append(dataSet[datas[j]][0])
            Y.append(dataSet[datas[j]][1])
        plt.scatter(X, Y, marker='o', color=color[i % len(color)], label=i)
    plt.legend(loc='upper right')
    plt.show()

主函数

def main():
    dataSet = loadDataSet("dataSet.txt")
    print(dataSet)
    C = DBSCAN(dataSet, 0.11, 5)
    draw(C, dataSet)

if __name__ == '__main__':
    main()

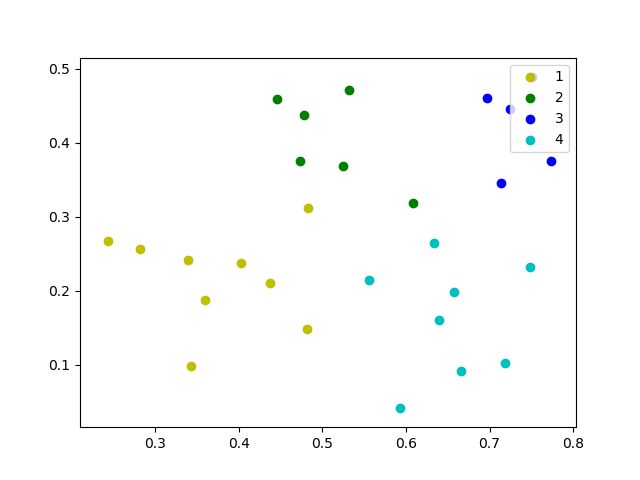
结果

python实例（二）

使用scikit-learn，代码如下

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
%matplotlib inline
X1, y1=datasets.make_circles(n_samples=5000, factor=.6,
                                      noise=.05)
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2,1.2]], cluster_std=[[.1]],
               random_state=9)

X = np.concatenate((X1, X2))
#展示样本数据分布
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
#eps和min_samples 需要进行调参
y_pred = DBSCAN(eps = 0.1, min_samples = 10).fit_predict(X)
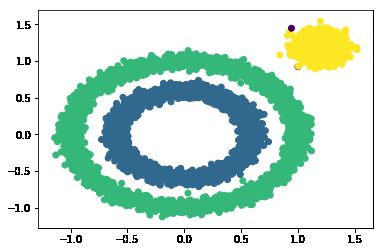
分类结果
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

结果

样本数据分布：

聚类结果：

---

更多机器学习干货、最新论文解读、AI资讯热点等欢迎关注”AI学院(FAICULTY)”
欢迎加入faiculty机器学习交流qq群：451429116 点此进群
版权声明：可以任意转载，转载时请务必标明文章原始出处和作者信息.

---

参考文献

[1]. 周志华，机器学习，清华大学出版社，2016
[2]. DBSCAN密度聚类算法- 刘建平Pinard - 博客园
[3]. 机器学习实战——python实现DBSCAN密度聚类