《算法导论》读书笔记(01)——ch02 算法基础【插入排序、归并排序】
《算法导论》第二章主要讨论了两个算法问题:插入排序和归并排序,在介绍两个算法的同时,对两个算法从运行效率上做了分析。最后对分治算法进行了做了简要介绍。下面对这两种算法从头开始分析,并用C语言和JAVA语言进行实现。
目录
1.插入排序
1.1 算法思路
1.2 算法实现
1.2.1 伪代码描述
1.2.2 C语言实现
1.3 算法分析与评价
2.归并排序
2.1 算法思路
2.2 算法实现
2.2.1 C语言实现
2.2.2 JAVA语言实现
2.3 算法评价
1.插入排序
1.1 算法思路
假设要对元素进行非递减排序。插入排序的运行方式为:对于一组待排序的数列,可认为数列的第一个元素是有序的,然后访问数列的第二个元素,将其与第一个元素比较,如果第二个元素比第一个元素大,则认为数列的前两个元素已经有序,继续访问第三个元素,如果第二个元素比第一个元素小,则交换前两个元素,使得前两个元素有序,接着访问第三个元素。访问第三个元素时,将其与它的前一个元素(第二个元素)比较,如果第三个元素大于第二个元素,则此时前三个元素便是有序的,如果第三个元素小于第二个元素,再将第三个元素与第一个元素比较,如果第三个元素大于第一个元素,则说明第三个元素的大小位于第一个元素与第三个元素之间,如果第三个元素小于第一个元素,则说明第三个元素是前三个元素中最小的,将之前第一个和第二个位置上的元素后移,将之前第三个位置上的元素放到第一个位置上即可。以此类推,向后扫描,假设数列共有n个元素,第i次循环后,前i个元素已经有序,第i+1次循环,将原数列i+1位置上的元素放到了有序的位置。
《算法导论》里面对于插入排序有一个很形象的例子:玩扑克牌
想一下我们玩扑克牌的时候,摸牌(摸到的牌都是已经打乱了的)并按照大小将牌整理好的过程,其实就是一个很形象的插入排序的例子。第一次先从桌子上摸一张牌,假设摸到了6,然后再摸一张牌,假设摸到了9,这比手中已有的牌的点数大,我们把摸到的9放到之前的6的右边。接着进行第三次摸牌,假设摸到了7,和手中已有的牌(6和9)进行比较,应该把7放到已有两张牌之间。接着第四次,假设摸到了3,和手中已有的牌比较,3应该放到6的前面。接着第五次假设又摸到了6(出现重复值),这时就把新摸到的6放到之前的6的相邻的左边或右边就好。就这样一直下去,每摸一张牌,就和手中已有的牌比较点数大小,并将新摸到的牌插入到合适的位置,直到摸完所有的牌,这时手中的牌都是已排序的。
特点:
(1)手中的所有牌都是已排序了的,桌子上还没有摸到的牌是待排序的;
(2)每次摸牌相当于一次循环,每次循环都将一个未排序的牌插入到了已排序的牌中,并且没有破坏其有序性;
(3)第一次摸牌后,手中只有一张牌,可将手中的一张牌看作是有序的;
说明:
每次摸到牌之后,需要和手中已有的牌比较,我们实际玩牌的时候就是随便瞅一眼就知道这张牌应该插入到什么地方,但是如果从计算机实现的角度看,这个过程应该是:拿着新摸到的牌,从手中最大的牌开始,一张一张地比较,如果位置不合适,将比较过的牌后移(给待插入的牌腾出一个位置),然后继续向前比较,不合适再后移腾位置,直到找到了一个合适的位置,将新摸到的牌插入即可。
再举个栗子:
下面的例子可能需要在纸上自己画一画写一写才能更清楚一些这个过程……
待排序的数列为:【 3 2 5 8 4 7 6 9 】,要求递增排列。
注:箭头所指的位置的前面的所有元素已经排序好。
【 3 2 5 8 4 7 6 9 】
↑
首先假定第一个元素为有序的,然后扫描第二个元素,第二个元素2,需要和第一个元素交换,交换后数列变成了:
【 2 3 5 8 4 7 6 9 】
↑
此时前两个元素有序了。第二个循环结束
然后扫描第三个元素5,比它的前一个元素3小,没毛病,继续下去是8,也没毛病,不需要交换,这个过程跑了两次循环,此时数列是:
【 2 3 5 8 4 7 6 9 】
↑
继续扫描,扫描到了4,小于8,需要把4和8交换,交换完成后如下:
【 2 3 5 4 8 7 6 9 】
然后比较4和5,这里还是得交换,交换后如下:
【 2 3 4 5 8 7 6 9 】
↑
最后比较4和3,4大于3,不需要交换,此次循环结束。
然后扫描到7,7大于8,需要交换,交换后7比5小,不需要交换,此次循环结束。
【 2 3 4 5 7 8 6 9 】
↑
然后扫描到6,原理同上,一直和前面相邻的元素比较并交换,直到前面相邻的元素小于6时停止。就会得到下面的序列:
【 2 3 4 5 6 7 8 9 】
↑
最后一个循环,处理9,该元素的位置没问题,不需要调整。循环结束,排序完成。
1.2 算法实现
1.2.1 伪代码描述
/*
伪代码描述插入排序算法,见《算法导论》 P10。
A :待排序数组
*/
for j = 2 to A.length
key=A[j]
i = j - 1;
while i>0 and A[i]>key
A[i+1] = A[i]
i = i-1
A[i+1] = key
end
1.2.2 C语言实现
下面用《数据结构与算法分析——C语言描述》上面的例程进行实现。
#include
#define N 8
/*
插入排序算法
data :待排序数组
length :数组元素个数
*/
void Insertion_Sort(int data[],int length)
{
int i,j;
int key;
for(i = 1 ; i < length ; i++){
key = data[i];
for(j=i;j>0 && data[j-1]>key;j--){
data[j] = data[j-1];
}
data[j] = key;
}
}
//主函数测试代码
int main(void)
{
int data[N] = {3,2,5,8,4,7,6,9};
int i;
Insertion_Sort(data,N);
for(i=0;i 1.2.3 JAVA实现
public class Sort{
/**
* 插入排序例程
* @param data 待排序数组
*/
public static void InsertionSort(int[] data) {
int j, key;
for (int i = 1; i < data.length; i++) {
key = data[i];
for (j = i; j > 0 && data[j - 1] > key; j--) {
data[j] = data[j - 1];
}
data[j] = key;
}
}
/**
* 输出一个数组中的值
* @param data
*/
public static void PrintData(int[] data) {
for (int i = 0; i < data.length; i++) {
System.out.print(data[i] + " ");
}
}
/**
* 主函数,测试函数
* @param args
*/
public static void main(String[] args) {
int[] data = { 3, 2, 5, 8, 4, 7, 6, 9 };
InsertionSort(data);
PrintData(data);
}
}
1.3 算法分析与评价
对于少量元素,插入排序是一个有效的算法。插入排序时间复杂度为O(n^2),空间复杂度为O(1),是一种稳定的排序。插入排序是原址排序输入的数的,只需要一个交换变量的临时空间。
插入排序是用来增量放大:在排序子数组data[0...i]之后,考察元素data[i+1],将其插入到data[0...i]的适当位置,构成有序数组data[0...(i+1)]。
暂时简单总结这些,后序遇到插入排序的特点了再来补充......
2.归并排序
2.1 算法思路
归并排序是基于分治法的思想,递归地对数组进行排序的。(所以要想真正理解归并排序的思路并进行实现,一定要理解递归操作)
归并排序算法的的操作可分为两个步骤,第一步是分解,第二步是合并。简单得说,分解操作是将待排序数组分解为一个个有序的数组,合并操作是将一个个有序数组合并为一个大的有序数组。我们常说的归并排序是二路归并排序,即每次分解过程是将数组分解为两个有序的数组,合并过程是将两个有序的数组合并为一个更大的有序数组。
依然可以用上面整理扑克牌的例子来说明一下归并排序的操作:
下面的描述纯手打,看起来可能比较繁琐,最好在纸上画一下这个过程,但相信认真读的话会理解归并排序的基础操作的,
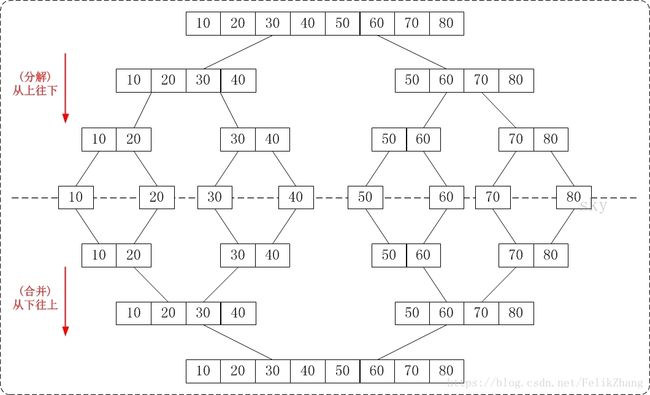
假定我们手里有8张打乱的扑克牌,我们现在要对其进行排序。首先进行分解,一直分解到每堆牌都是有序的为止,第一次,将8张牌分成两堆,每堆4张,这时发现每堆牌依然不是有序的,所以分别拿起已经分解了一次的两堆牌继续分解,4张牌分成两堆,每堆2张,一共4堆,假设这时每堆牌依然不是有序的,那就继续分,分成了每堆1张,这时候一定是有序的了,分解操作结束,此时8张牌被分成了8堆,每堆1张。下面是合并操作,首先拿起两堆(共2张)牌,按照大小进行排序,然后放下。再拿起还没排序的两堆牌,排序,放下,这样操作四次,原先的8堆牌变成了四堆牌,每堆2张,并且每堆的2张都是排序好了的。下面在这4堆中再拿起两堆,这两堆牌中各有2张,并且均已排序,现在要做的就是把这4张牌进行排序,这里实际是将两个有序序列合并为一个有序序列的基本操作。合并结束后,现在的局面是,有三堆牌,都是已排序了的,其中一堆4张,另外二堆各2张,下面拿起每堆2张的那两堆,依然是个有序序列合并的操作,完成之后,剩下两堆(各4张)有序的牌了,继续将两堆有序的牌合并成一堆有序的牌即可。这时候就只剩下一堆牌(8张)了,并且这堆牌是有序的,排序完成。
下面用一个图展示一下上面描述的过程(图片来自网络,侵删)。
2.2 算法实现
如上所述,归并排序分为两个步骤,算法的思想是基于递归的,因此实现也是通过递归的方法实现的。其中递归中调用的过程就是分解的过程,调用结束返回的过程就是合并两个有序序列的过程。下面首先实现合并两个有序序列的过程,即两个有序序列合并为一个有序序列的操作,然后利用该操作的思想,实现归并排序算法。
2.2.1 C语言实现
Part 01:两个有序序列合并为一个有序序列
不多说了,C语言的基础操作,直接上代码了。
#include
#include
int* Merge(int dataA[],int lengthA,int dataB[],int lengthB)
{
int i = 0,j = 0,k = 0;
int* temp = malloc(sizeof(int)*(lengthA+lengthB));
while(i Part 02:无序序列的分解操作
分解操作的过程上一节的例子中已经有较详细的说明,这里基于分治思想,递归的方式进行实现。不多说了。
完整的归并排序C语言实现代码如下:
说明:下面的代码参考了《算法导论》(机工)以及《数据结构与算法分析——C语言实现》(机工)这两本书上的内容。C语言实现起来还是有点小麻烦的,像数组长度之类的值,还有那个缓存数组,调用函数的时候得到处传递……可能有更好的实现吧,以后遇到了贴上来。
#include
#include
void Merge(int data[],int left,int mid,int right,int *temp);//合并两个升序列的操作
void MergeSort(int data[],int *temp,int left,int right);//归并排序
void PrintData(int data[],int length);//数据输出
int main(void)
{
int data[8] = {3,2,5,8,4,7,6,9};
int length = 8;
int i;
int *temp = NULL;
temp = malloc(sizeof(int)*(length));
MergeSort(data,temp,0,length-1);//归并排序操作
PrintData(data,length);
free(temp);
return 0;
}
//合并两个升序列的操作
void Merge(int data[],int left,int mid,int right,int *temp)
{
int i = left,j = mid+1,k = left;
while(i <= mid && j <= right){//处理公共部分
if(data[i] < data[j]){
temp[k++] = data[i++];
}
else{
temp[k++] = data[j++];
}
}
while(i <= mid){//处理数组A可能的剩余部分
temp[k++] = data[i++];
}
while(j <= right){//处理数组B可能的剩余部分
temp[k++] = data[j++];
}
//将排序完的序列写入原始数组中
for(i = left;i <= right;i++){
data[i] = temp[i];
}
}
//归并排序
void MergeSort(int data[],int *temp,int left,int right)
{
int mid;
if(left < right){
mid = (right+left)/2;
MergeSort(data,temp,left,mid);
MergeSort(data,temp,mid+1,right);
Merge(data,left,mid,right,temp);
}
}
//数据输出
void PrintData(int data[],int length)
{
int i;
for(i = 0 ; i < length ;i++){
printf("%d\t",data[i]);
}
printf("\n");
} 2.2.2 JAVA语言实现
public class Sort{
public static void main(String[] args) {
int[] data = { 3, 2, 5, 8, 4, 7, 6, 9 };
int[] temp = new int[data.length];
int length = 8;
MergeSort(data, temp, 0, length - 1);// 归并排序操作
PrintData(data, length);
}
// 合并两个升序列的操作
public static void Merge(int[] data, int left, int mid, int right, int[] temp) {
int i = left, j = mid + 1, k = left;
while (i <= mid && j <= right) {// 处理公共部分
if (data[i] < data[j]) {
temp[k++] = data[i++];
} else {
temp[k++] = data[j++];
}
}
while (i <= mid) {// 处理数组A可能的剩余部分
temp[k++] = data[i++];
}
while (j <= right) {// 处理数组B可能的剩余部分
temp[k++] = data[j++];
}
// 将排序完的序列写入原始数组中
for (i = left; i <= right; i++) {
data[i] = temp[i];
}
}
// 归并排序
public static void MergeSort(int[] data, int[] temp, int left, int right) {
int mid;
if (left < right) {
mid = (right + left) / 2;
MergeSort(data, temp, left, mid);
MergeSort(data, temp, mid + 1, right);
Merge(data, left, mid, right, temp);
}
}
// 数据输出
public static void PrintData(int[] data, int length) {
int i;
for (i = 0; i < length; i++) {
System.out.print(data[i]+" ");
}
System.out.println();
}
}
2.3 算法评价
归并排序的时间复杂度是O(NlogN),它是递归算法一个很好的实例。虽然归并排序运行时间很快,所使用的比较次数几乎也是最优的,但是它很难用于主存排序,主要问题实在合并两个顺序序列的操作中需要线性的附加内存,同时拷贝过程需要线性附加的时间。不过由于归并排序运用了分治思想,在大数据的排序中还是有很不错的应用的,