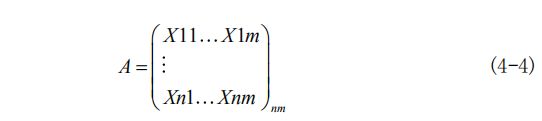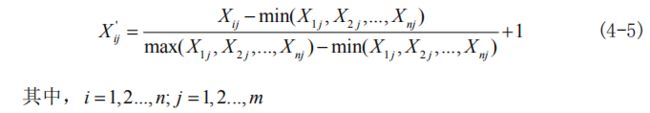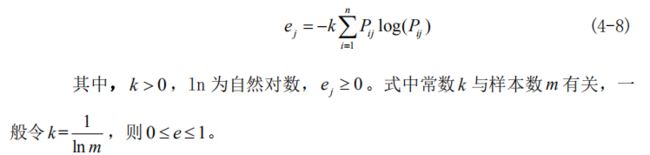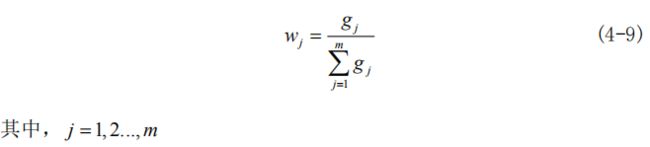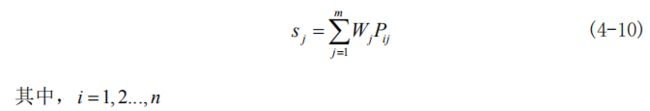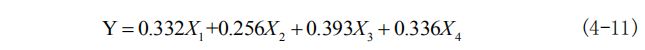数学建模历年真题分析

                              2018年C题：对恐怖袭击事件记录数据的量化分析

• 任务1：依据危害性对恐怖袭击事件分级

影响因素：人员伤亡、经济损失、事件发生的时机、地域、针对的对象

目标：

1、将附件1给出的事件按危害程度从高到低分为一至五级。

2、列出近二十年来危害程度最高的十大恐怖袭击事件。

3、给出表1中事件的分级。

解题思路：

建立基于权重分配的事件结果量化分级模型。根据数据特 征选出了 4 个指标（袭击事件死亡总数、受伤总数、财产损失价值以及人质或绑 架总数），通过中位数插值法填充变量中的缺失值，计算 4 个指标的 KMO 值为 0.714，为了获得更加精确的指标权重，分别使用主成分分析方法和熵值系数法 对模型进行求解，获得的指标权重值分别为（0.246,0.196,0.301,0.257）和 （0.108,0.137,0.429，0.326），然后利用 K-means 聚类方法对事件结果量化值 进行五项聚类，实现数据的量化分级。

模型建立（基于权重分配的量化分级模型）

1、分析出事件危害等级的四项评价指标：袭击事件死亡总数X1、受伤总数X2、财产损失价值X3、人质或绑架总数X4。

2、数据处理：将附件 1 中的数据做冗余和插值填充等处理。得到处理后的完整数据附件 A。

在死亡总数方面，将附件 1 中的死亡总数缺失的袭击事件去除，未考虑到后续分析中；

在受伤总数方面，将附件 1 中的受伤总数缺失的袭击事件去除，未考虑到后续分析中；

在人质或绑架总数方面，1、本文将人质或绑架的受害者标签为-9（不知道受害人是否被劫持或绑架）的袭击事件去除； 2、将人质或绑架的受害者标签为 0（受害者没有被劫持或绑架），且人质或绑架总数为空值的袭击事件的人质或绑架总数置为 0； 3、在上述处理的结果上，针对人质或绑架总数标签为-99（人质的数量不知道或不确定）的袭击事件，本文利用处理后数据的人质或绑架总数的中位数，来为作为此类事件的人质或绑架总数做插值填充。

在财产损失价值方面，也是中位数插值填充。

3、建立基于权重分配的事件结果量化分级模型， 量化结果 Y 如式（4-1）所示。

模型求解

为了求解上式中的权重的精确值，用基于主成分分析的权重确定和 K-means聚类算法对量化模型进行权重求解的同时（法1），还用了基于熵值的权重确定和 K-means 聚类算法对量化模型的权重进行了求解（法2）。

法1：基于主成分分析权重确定和 K-means 聚类的求解：根据主成分分析的权重确定，得到事件结果Y的量化表达式，再通过对Y值进行 K-means 聚类，聚成 5 个类别等级。通过对聚类结果的分析， 以各个类别等级的量化结果值，划定 5 个级别的危害影响值的判定范围。

主成分分析：把原本相关性较强的变量X1、X2...Xn重新组合，生成 少数几个彼此不相关的变量F1、F2...Fm。

F1 = a11*X1 + a21*X2 +...+ an1*Xn + a*e1。

F2 = a12*X1 + a22*X2 +...+ an2*Xn + a2*e。

...

Fm = a1m*X1 + a2m*X2 +...+ anm*Xn + am*e。

其中F1、F2...Fm叫做主成分，依次是第一主成分、第二主成分...第 m 主成分。

具体实现可以看这篇博客：https://blog.csdn.net/qq_20913021/article/details/59131757（突然发现学长的论文和这个一样...）

更详细的一篇：https://blog.csdn.net/qq_32925031/article/details/88540234（太累赘，上面那个链接更好，哈哈）

K-means 聚类：将数据按照内部存在的特征将数据划分为多个不同的类别， 使类别内的数据比较相似，类别之间的数据相似度比较大，其目标是最小化平方误差 。

算法流程：

(1)从数据中选择 k 个对象作为初始聚类中心;

(2)计算每个聚类对象到聚类中心的距离来划分；

(3)再次计算每个聚类中心

(4)计算标准测度函数，直到达到最大迭代次数，则停止，否则，继续操作。

法2：基于熵值权重确定和 K-means 聚类的求解

熵值法：根据各项指标观测值所提供的信息的大小来确定指标权重。熵是对不确定性的一种度量，信息量越大，不确定性就越小，熵也就越小；信息量越小， 不确定性越大，熵也越大。根据熵的特性，可以通过计算熵值来判断一个事件的 随机性及无序程度，也可以用熵值来判断某个指标的离散程度，指标的离散程度 越大，该指标对综合评价的影响（权重）越大，其熵值越小。

算法流程：

(1)数据矩阵

Xij为第i个方案第j个指标的数值。

(2)数据的非负数化处理：在熵值法的使用过程中，需要对数据进行非负化处理。此外，为了避免求熵值时对数的无意义，需要对数据进行平移。

对于越大越好的指标：

对于越小越好的指标：

(3)计算第 j 项指标下第 i 个方案占该指标的比重。

(4)计算第 j 项指标的熵值。

(5)计算第 j 项指标的差异系数。

(6)求权数。

(7)计算各方案的综合得分 。

求解结果

法1：在主成分分析权重确定和 K-means 聚类的模型求解中，针对袭 击事件死亡总数、受伤总数、财产损失价值以及人质或绑架总数四项评价指标， 使用 SPSS （一个数据分析软件）对主成分权重的求解做相应处理。

已知1、【表 4-3 KMO 检验标准】根据求得的KMO 值判断适合主成分分析的程度。

已知2、【表 4-4 解释的总方差】前 3 个主成分对应特征根分别为 2.208、1.997 和 1.537， 均大于 1，提取前 3 个主成分的累计方差贡献率达到 93.554%，超过 80%。因此， 前 3 个主成分基本可以反映全部指标的信息，可以代替原来的 4 个指标（袭击事 件死亡总数、受伤总数、财产损失价值以及人质或绑架总数）。

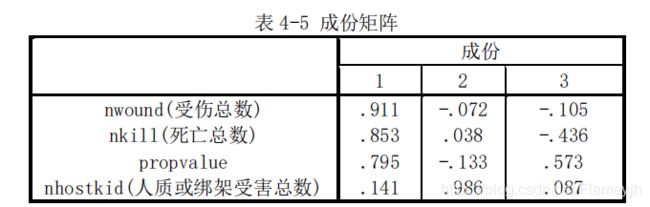
已知3、【表 4-5 成份矩阵】由表 4-5 可知第一主成分、第二主成分以及第三主成分对原来指标的载荷 数，如第一主成分对 nwound(受伤总数)的载荷数为 0.911。

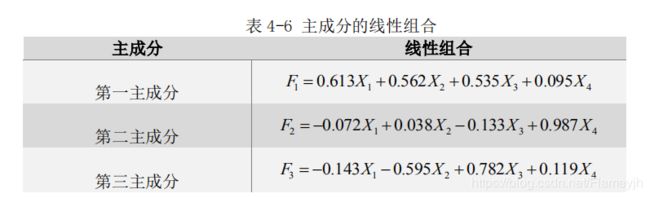
计算1、【表 4-6 主成分的线性组合】根据上面的表就可以求出指标在各主成分线性组合中的系数，使用表 4-5 的载荷数除以表 4-4 中对应的特征根的开方，（比如0.911/根号下2.208 = 0.613）。按此方法，基于表 4-4 和表 4-5 的数据， 可分别计算出各指标在三个主成分线性组合中的系数，得到的三个主成分线性组 合如表 4-6

计算2、结合表4.4的方差贡献率，对指标在这3个主成分线性组合中的系数做加权平均，得到最后的权重。

计算3、指标权重的归一化，由于所有指标的权重值之和为 1，因此指标权重 需要在综合模型中指数系数的基础上归一化，得到最终的事件结果量化值 Y 的表 达式如式（4-12）所示：

最后，计算全部量化结果Y，保存到附件B。

将处理后的所有事件量化结果Y使用 K-means 聚类到 5 个簇。

对聚类后的每个等级类别中量化值 Y 进行排序,得到每个簇的最大值和最小值。

法2：在熵值权重确定和 K-means 聚类的求解方法中，利用式（4-10）结合本任务数据，得到事件量化结果各指标权重。

后续使用 K-means 聚类到 5 个簇，与法1相同。

• 任务2：依据事件特征发现恐怖袭击事件制造者

目标：

1、针对在2015、2016年度发生的、尚未有组织或个人宣称负责的恐怖袭击事件，运用数学建模方法将可能是同一个恐怖组织或个人在不同时间、不同地点多次作案的若干案件归为一类。

2、对应的未知作案组织或个人标记不同的代号，并按该组织或个人的危害性从大到小选出其中的前5个，记为1号-5号。

3、对表2列出的恐袭事件，按嫌疑程度对5个嫌疑人排序。

解题思路：

整体：根据数据特征和数据间的关系，本文选取 22 个分类指标，利用已知发动者的事件对 SVM 分类器进行训练，获得 2015 至 2016 年恐怖组织或个人的案件归类，当置信度大于 50%的事件才归到相应的类别。其次利用所有已归类的数据训练 DBSCAN，通过 ARI 指数选取 DBSCAN 的半径大小为 8，并使用此半径利用 DBSCAN 算法对未知发动者的事件进行聚类分析，并基于准确率、召回率、 F 值说明建立的模型的有效性。

分步：

第1问、根据每次事件的不同特征对附件 1 中的相应数据建立分类、聚类模型，对同 一恐怖组织或个人的恐怖袭击事件做分类分析，可以得到某一恐怖团体的作案特征，然后将未知恐怖袭击发动者的案件映射到已知作案者的案件中，可以判定部分未知案件最可能的发动者。对于无法匹配的事件，可以使用 DBSCAN 算法进行 聚类分析，将其定义为未知的作案组织或个人。

第2问、使用任务一中的事件结果量化模 型，对本任务涉及到的事件按组织进行量化结果的求和计算，从而得到前五个组织或个人。

第3问、对于事件嫌疑度的排序，可以将事件映射到本任务涉及到的所有组织中，通过置信度的大小对 5 个嫌疑人进行排序。

模型建立（基于 SVM 和 DBSCAN 的非线性模型的建立）

数据处理：

依照任务一中对数据处理的方式，对 2015 年和 2016 年数据进行了相应的冗余数据的去除以及 缺失值的插值填充。选取国家、武器类型、地理编码特征等 22 个 指标。处理后的全部事件存为附件 H。

为了探究同一组织或个人的作案特征，建立基于 SVM 和 DBSCAN 的分类模型。

原因：

可以处理非线性多变量的关系，并不用考虑变量之间的潜在关系。它的特点是将实际问题通过非线性变换到高维特征。在高维空间中进行线性分类模型来实现空间的非线性分类。

基于 SVM 和 DBSCAN 的非线性模型：

模型求解

首先建立基于支持向量机的分类模型，将选取的实际问题的变量通过非线性变换转换成高维特征，然后在高维空间中对这些特征再进行非线性分类。以此找出同 一犯罪组织的作案特征，并将该组织所有的犯案信息归为一类。

SVM：对于SVM的训练和求解部分数学公式比较多，这里不详细介绍。

其次对剩余Unknown事件，使用DBSCAN 聚类算法。DBSCAN好处是可以在事先不知道数据有多少类特征的情况下， 对数据进行合理的类别划分。原理是由密度可达关系导出的最大密度相连的样本集合，即特征很相似的数据簇。

DBSCAN：https://blog.csdn.net/zhouxianen1987/article/details/68946169

原理：该算法利用基于密度的聚类的概念，即要求聚类空间中的一定区域内所包含对象（点或其他空间对象）的数目不小于某一给定阈值。该方法能在具有噪声的空间数据库中发现任意形状的簇，可将密度足够大的相邻区域连接，能有效处理异常数据，主要用于对空间数据的聚类。

DBSCAN聚类算法三部分：

1、        DBSCAN原理、流程、参数设置、优缺点以及算法；

http://blog.csdn.net/zhouxianen1987/article/details/68945844

2、        matlab代码实现； 

blog：http://blog.csdn.net/zhouxianen1987/article/details/68946169

code：http://download.csdn.net/detail/zhouxianen1987/9789230

3、        C++代码实现及与matlab实例结果比较。

blog：http://blog.csdn.net/zhouxianen1987/article/details/68946278

code：http://download.csdn.net/detail/zhouxianen1987/9789231
 

求解结果

SVM部分：在 2015 年至 2016 年间全球共发生 28556 起恐怖袭击事件，其中已知袭击发 动者的案件数量为 15360 起，根据恐怖组织名称或个人名称将其分组，作为 SVM 分类模型的训练数据，其中将 80%数据作为训练集，用于学习每个恐怖组织或个 人的作案特征；剩余的 20%作为测试集数据，用以检测模型的分类准确度。

DBSCAN 部分：算法在很大程度上依赖于选取的聚类半径，为尽可能得到最准确的聚类结果，本文选取 2015 年至 2016 年除了 Unknown 恐怖事件发动者的所有恐怖事件进行拟合，得到最优聚类半径为8（此时ARI 指数取得最大值）。然后把剩余的未知恐怖事件发动者的案件输入到基于密度聚类的模型中进行聚类，将具有相同作案特征的案件归为一类。

• 任务3 对未来反恐态势的分析

目标：

依据附件1并结合因特网上的有关信息，建立适当的数学模型，研究近三年来恐怖袭击事件发生的主要原因、时空特性、蔓延特性、级别分布等规律，进而分析研判下一年全球或某些重点地区的反恐态势。

思路：

第1步：对事件发生时间和事件的量化结果建立时间序列模型。采用 ARIMA 时间序列模型。原因是数据波动很大。

第2步：对事件发生时间和单位时间内事件发生的次数建立时间序列模型。采用指数平滑法。原因是数据波动不大。

数据处理：

依照任务一中对数据处理的方式，对三年数据进行了相应的冗余数据的去除以及缺失值的插值填充。将同一个月内的所有事件的量化结果求和，作为当月的袭击事件影响结果值。将事件发生次数以月为单位进行统计。处理后存为附件E。

做好以上分析工作以后可以直接使用spss软件的到结果。这里就不展示了。

用SPSS建立ARIMA预测模型：https://jingyan.baidu.com/article/48a42057e664bda9242504f8.html

如何使用SPSS做时间序列分析？（包括指数平滑法和ARIMA）https://jingyan.baidu.com/article/6b182309a977bdba58e159d4.html

• 任务4 数据的进一步利用

目标：

你们认为通过数学建模还可以发挥附件1数据的哪些作用？给出你们的模型和方法。

思路：

找到一个合适的“最恐怖”组织（比如发起恐怖事件次数最多的恐怖组织），对 “最恐怖”组织每次发起恐怖事件时间间隔的数据进行分析，并预测该组织间隔多长时间发起下次恐怖事件。

用SPSS建立ARIMA预测模型：https://jingyan.baidu.com/article/48a42057e664bda9242504f8.html

上面的链接可以实现论文中所有步骤（如下）

1、用spss建立基于事件发生时间间隔的 ARIMA 时间序列模型。

2、spss能得到相关的差分次数，用它做模型的平稳性检验。

3、得到ARIMA模型的拟合图和观测值，说明拟合情况。

4、得到基于时间间隔的真实值与预测值的残差图，说明模型误差。

5、得到具体时间预测，能明确预测出该组织的爆发恐怖事件的日期， 这个预测能有效打击恐怖活动且具有十分重要的意义。

 

完结撒花。。。。。。