Dijkstra 新手向攻略(原版及堆优化) 初学者点进来
Dijkstra(迪杰斯特拉)是一个非常基础的算法,也是最常用的,被用于求解图论的最短路问题。但看网上好多教程都写的很复杂,我争取用最易懂的对新手友好的语言来解释清楚这个算法。
使用范围
求解有向带边权图的最短路问题,给定起点,给定边权和起止点,求到达每一个点的最短距离。
算法概述
从起点(由输入给出)开始,遍历所有的和起点直接相连的点,比如现在我们假设1号是起点。
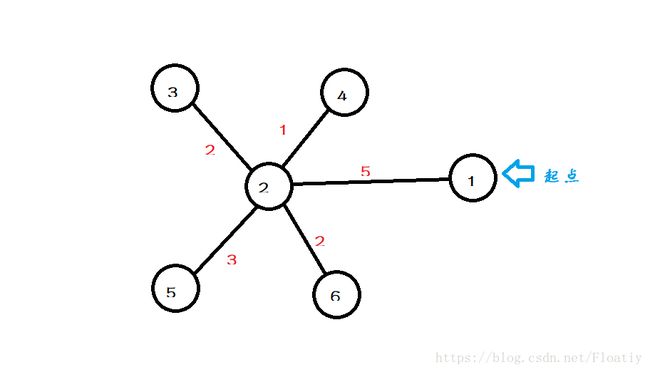
拿上面这张图举例子
首先,把除了起点以外的点的距离都初始化为无限大(INF)(i到起点距离用dist[i]表示)
dist[1] 0
dist[2] INF
dist[3] INF
dist[4] INF
dist[5] INf
dist[6] INF和1直接相连的点是2,那么我们现在把2到起点的距离处理一下,应该是5
dist[1] 0
dist[2] 5
dist[3] INF
dist[4] INF
dist[5] INf
dist[6] INF以此类推,每次把与 已确定距离的点 相连的点的dist值处理一下就好了
最后我们可以得到下面这张表:
dist[1] 0
dist[2] 5
dist[3] 5+2=7
dist[4] 5+1=6
dist[5] 5+3=8
dist[6] 5+2=7看上去你已经理解Dijkstra算法的大体思路了,看上去很简单,任何困难的事情都是一点一点做成的。
那么,如果我的图变成这样呢?
我可没有保证没有环
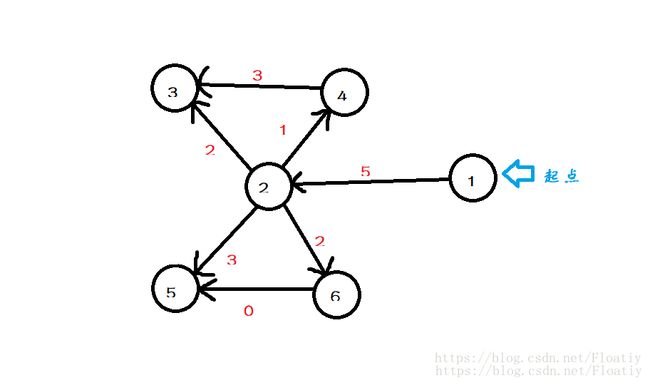
我加了几条边,产生了环,(没错那条边边权就是0)
这样带来的问题就是,每一个点将会有不止一种方法到达。
那我们到底应该怎么办?很简单啊,选到达方式中最优的方案。
我再来手动模拟一下,,,(前半部分和前一个例子相同)
[重点]每一次处理一个点(简称 这个点)时,我们需要枚举它可以到达的点(简称 那个点)的dist值,如果当前算出的距离比那个点原来记录下来的dist值小,就把那个点的dist赋值成当前算出的那个点到起点的距离。
首先,把除了起点以外的点的距离都初始化为无限大(INF)(i到起点距离用dist[i]表示)
我们再引入一个叫vis的数组来记录一个点是否被处理过
dist[1] 0
dist[2] INF
dist[3] INF
dist[4] INF
dist[5] INf
dist[6] INF和1直接相连的点是2,那么我们现在把2到起点的距离处理一下,应该是5
dist[1] 0
dist[2] 5
dist[3] INF
dist[4] INF
dist[5] INf
dist[6] INF这时候就不同了,我们可以看到,2号点连着4条边,这时
Dijkstra算法要求我们从中按到起点距离的大小 从小到大依次处理这些点。
so,我们应该处理4号点了,这样的话,可以得到下表
dist[1] 0
dist[2] 5
dist[3] dist[4]+3=9
dist[4] dist[2]+1=6
dist[5] INF
dist[6] INF按顺序,我们处理完4号点该处理3号点了,但我们发现3号点已经有dist值了(9),但我们现在计算出来3号点距离应该是dist[2]+2=7,比原来的要优,所以我们将dist[3]赋值为7。这个操作叫“更新”。
那么我们就可以依次将所有点处理完了。
最后得到:
dist[1] 0
dist[2] 5
dist[3] 7
dist[4] 6
dist[5] 7
dist[6] 7那么,现在你已经理解了基础的Dijkstra了。
code
//by floatiy
#include
}
int x,y,z;
for(int i=1;i<=m;i++)//输入边
{
scanf("%d%d%d",&x,&y,&z);//依次是 起点 终点 边权
l[i].pre=x,l[i].to=y;
l[i].w=z;
a[x].num++;//起点的出度+1
a[x].about.push_back(i);//记录这个边
}
dist[s]=0;//起点距离设成0
node=s;//从起点开始处理
while(!vis[node])
{
vis[node]=1;//已经处理过了
minn=INF;//每次记得让minn变成无限大
//这里比较难懂,因为我奇怪的双结构体存图方法,我不会前向星。。。
//总之下面这个循环就是枚举一下每一条从node节点出去的边,然后处理它们所连的点的dist
for(int i=0;i//枚举每条从这个点出去的边在这个点的所有出边中的编号i
{
if(dist[l[ a[node].about[i] ].to] > dist[node]+l[ a[node].about[i] ].w)
//如果出边连到的那个点到起点的距离
//比
//现在这个点到起点的距离+这条边的边权
//要大
//我们就更新连到的这个点的dist值
dist[l[ a[node].about[i] ].to]=dist[node]+l[ a[node].about[i] ].w;
}
node=find_new();//做完一个点,找下一个点
}
for(int i=1;i<=n;i++)
printf("%d ",dist[i]);
}
大家尽量去理解,我这个双结构体真的不好理解,建议大家换一种存图的方法。
我太弱了qwq,不会前向星。
堆优化介绍
大家想想,上面的程序有哪里可以大幅度节约时间呢?
每个点的处理是必要的
输入输出也找不到能大幅度降低时间复杂度的办法
那么?
没错,在我们查找新节点的时候,采取的是将每个点都枚举一遍的办法,显然这样会让时间复杂度变成n^2,但我们有一个叫堆的好东西,emmm如果不知道堆排序可以看一下这个,原理很简单的:堆排序
我们建一个小根堆,这样就能很方便的在nlogn的时间内找出最小值了
或者。。如果懒的话可以用一个东西,叫优先队列(STL里的priority_queue)
写一份代码:
这个是在上一份代码的基础上改的,故不加备注了,stl的友元函数重载我也不是很懂,,,大家可以baidu一下。。。
//Dijkstra 堆优化
#include q;
void add(int x,int y,int z)
{
cnt++;
l[cnt].to=y;
l[cnt].w=z;
l[cnt].next=head[x];
head[x]=cnt;
}
int main()
{
cin>>n>>m>>s;
int x,y,z;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
for(int i=1;i<=n;i++) a[i].dis=INF,a[i].no=i;
a[s].dis=0;
q.push(a[s]);//忘了扔起点 出锅*1
int cur=s;
while(!q.empty())
{
cur=q.top().no;
q.pop();
if(vis[cur]) continue;//注意是看cur是否处理过,而非看to是否处理过 出锅*2
vis[cur]=1;
for(int i=head[cur];i;i=l[i].next)
{
if(a[l[i].to].dis > a[cur].dis+l[i].w)
{
a[l[i].to].dis=a[cur].dis+l[i].w;
q.push(a[l[i].to]);
}
}
}
for(int i=1;i<=n;i++)
{
printf("%d : %d\n",i,a[i].dis);
}
return 0;
}