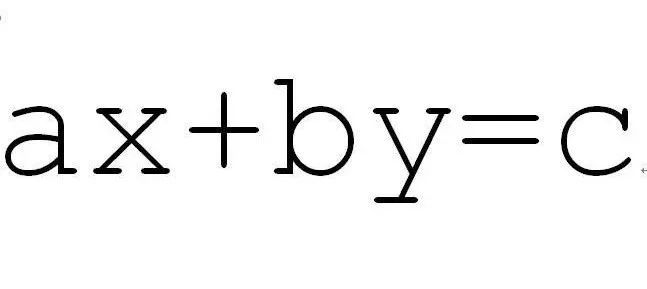数论的世界

说起数论，这是一个很神奇的学科——因为它的内涵会因不同的人而变得简单或复杂。

对于小学生而言，数论就是整数、小数、分数和加减乘除，理解起来不费吹灰之力。

对于数学大家们而言，数论却是诸如费马定理、哥德巴赫猜想、黎曼猜想等复杂而神秘的问题。一个不小心，到死也不知道答案。

那么，数论究竟是如何发展起来的呢？别着急，拿好小本本，给大家一一道来！

数论的起源，要追溯到古希腊时期。那时人们在拥有“数”的概念之后，自然而然地就会接触到一些“数”的性质。而第一个研究这些“数”的性质的学者，是古希腊一位著名的哲学家——毕达哥拉斯。

毕达哥拉斯：生得早就是好，什么事情都先讲我

毕达哥拉斯和他的学派秉承着“万物皆数”的哲学思想，为了研究眼前的世界，他们精力都放到了对正整数的研究上。（注意，毕达哥拉斯所指的“数”，只限于正整数）

他们将正整数分为奇数和偶数，研究了奇偶数之间四则运算的规律，还提出了“亲和数”、“完全数”等概念，并给出了“220”和“284”这对亲和数。

所谓的“亲和数”，是指一对正整数，它们各自的全部约数之和（本身除外）与对方相等。毕达哥拉斯曾说：“朋友是你灵魂的倩影，要像220与284一样亲密。”

至于“完全数”，则是指一个正整数，它的全部约数之和（本身除外）等于它本身。第一个完全数是6，第二个完全数是28，第三个完全数是496。

但是毕达哥拉斯对正整数的研究，还出于占卜等宗教活动的需要，因此具有较为浓厚的宗教神秘色彩，没有严格的概念定义和数学论证——不过这个缺点，在后人的著作中得到了弥补。

欧几里得是毕达哥拉斯之后，把对正整数的研究继续往前推进的古希腊学者。

欧几里得：结果烂摊子还是要我来收拾……

在自己的著作《几何原本》中，欧几里得首次给出了因数、倍数、素数、互素等基本概念的精确定义，并对所得到的结论进行了详细的证明，从而使数论的研究严密化。

《几何原本》中，欧几里得提出了一些很重要的量化定理，比如说“完全数定理”：

如果2^n-1是素数，那么2^（n-1）·（2^n-1）是完全数。

后来的数学家欧拉证明了这个定理，并且据此给出了所有的偶完全数。

当然，欧几里得对数论的贡献并不止使数论的研究严密化，还有发现素数在整数理论中的重要价值和基础地位。他不仅证明了关于自然数和素数之间的积性关系，还运用归谬法证明了素数个数的无穷性，提出了计算最大公约数的算法——辗转相除法。

辗转相除法：设两数为a、b(a≥b)，求a和b最大公约数 （a，b）的步骤如下：

(1)用a除以b(a≥b)，得 a/b=q……r1 。

(2)若 r1=0，则（a，b）=b；

(3)若 r1不等于0，则再用b除以 r1,：b/r1=q……r2。

(4)若 r2=0，则 （a，b）=r1；若 r2不等于0，则继续用 r1除以 r2，......，如此下去，直到能整除为止。其最后一个余数为0的除数即为 （a，b） 的最大公约数。

欧几里得的研究，形成了初等数论的雏形，同时也提出了一个贯穿初等数论的命题：素数的普遍公式——同时，这个命题也直接催生了解析数论。

现在，让我们的目光继续跟着时间来走吧。在欧几里得之后，另一位数学家丢番图，为初等数论开拓了一片新领域——不定方程问题。

所谓不定方程，是指未知数的个数多于方程个数，且未知数受到某些限制（如要求是有理数、整数或正整数等等）的方程或方程组。丢番图将自己的研究写成了一本书——《算术》，而这本书也开启了中世纪的初等数论研究。

值得一提的是，在丢番图提出不定方程问题的同时期，中国也挖掘了数论的另一个领域——同余理论。《孙子算经》里面记载的“物不知数”问题，就涉及到了同余理论的研究。而宋朝秦九韶所提出的“大衍求一术”，则是比后来的高斯早了几百年，提出了具体且完备的求一次同余式组的方法。

所以说，中国古代在数论的研究上，也是辉煌一时啊。

好了，让我们的视线再回到欧洲。在丢番图之后，初等数论研究的大旗，就传到了一位“业余”的数学家——费马的手上。（怎么又是您老人家……）

费马：真是不好意思，兴趣爱好广泛就是这样的

费马对于初等数论的研究兼有欧几里得和丢番图的影子。他一生提出了形形色色的定（cai）理（xiang），最著名的莫过于“费马大小定理”：

费马小定理：如果p是素数，a与p互素，那么a^p-a可以被p整除。

费马大定理：方程x^n+y^n=z^n对于任意大于2的自然数n无整数解。

这两个定理皆是在费马阅读丢番图的《算术》时所提出的，尤其是费马大定理，基本上延续了丢番图从不定方程来发展数论的思想。但是费马的其他猜想，却也有欧几里得的影子，如他给出的“费马数”（一种“素数的普遍公式”）：

与欧几里得对“完全数定理”的描述极为相似。可以说，初等数论在费马手里，隐隐表现出一种成为一个体系的趋势。

但遗憾的是，这种趋势并未成为现实。费马之后的欧拉，尽管推翻了“费马数”的结论（“费马数”即为素数的普遍公式），证明了费马小定理的正确性，并在《代数指南》中使用“无限下降法”，使之成为数论研究中很重要的方法技巧之一，却依旧未能将众多理论统一起来，使初等数论成为一个完备的理论体系。

在18世纪快要结束的时候，数学家们发现，初等数论的研究似乎已经走到了尽头：整数数域的性质已经被研究得差不多了，接下来该怎么办？

一位天才的出现，让数论的研究从死胡同中走了出来，他就是德国的数学王子——高斯。

高斯：终于轮到我出场了

而让高斯带领数论走出“死胡同”的，是他对于“二次互反律”的研究。

二次互反律，是一个用于判别二次剩余，即二次同余方程之整数解的存在性的定律。

高斯非常欣赏这个定律，他一生中至少给这个定律作了8种完全不同的证明，并且试图将它推广到三次和四次互反律。

但是经过研究后，高斯发现，如果要使三次和四次的剩余理论和二次剩余理论那样简洁优美，里面所涉及到的数就必须超出整数的范围，引进复整数（即形如a+bi，其中a、b均为整数的复数）。

经过一番思考与研究之后，高斯决定将复整数引入到数论的研究当中，并且惊奇地发现，一些初等数论里面的定理，在复整数中依旧成立。如在初等数论中，每一个整数都能够唯一地分解为素因子的乘积，这个定理依旧在复整数中成立。

如此一来，高斯打破了初等数论的困境，将数论带到了一个更广阔的天地——复整数中来。

在高斯之后，库默尔和戴德金将高斯的研究成果成功地推广为一个全新的数论——代数数论。

库默尔

戴德金

在代数数论中，研究的对象从正整数变成了代数整数。关于一个数是不是代数整数，代数数论是这样定义的：

如果α是一个有理数多项式：的根，则称α为一个代数数。若P(x)的系数都是整数，则称α为一个代数整数。

除去代数整数，代数数论的研究对象还有代数数域。

关于代数数论是如何具体研究的，超模君就不展开讲了，不过模友们需要了解的一点是：直到1898年，德国数学家希尔伯特在对各代数数域的性质加以系统总结和发展后，前后经过了百多年的时光，经典代数数论才真正定型。

相比起初等数论，代数数论无疑涵盖更广，而且系统性更强，这是代数数论工作者们最值得自豪和被称赞的地方。

如果说代数数论是数论广度的一个拓展的话，那么解析数论可以说是对于数论研究方法的一次革新了。

解析数论的源头，可以上溯到欧拉。

欧拉：终于可以露脸了

早在1737年的时候，欧拉在研究无穷级数和无穷乘积的收敛性时，发现对于大于1的实数s，有等式：

其中无穷乘积中p是所有素数，这个等式揭示了素数p和自然数n之间的积性关系，也就是欧几里得所曾经证明过的，而且如果令s=1，则可以得出素数是无限多个的结论。这是数论第一次与解析形式相关联起来的例子。

在欧拉之后，狄利克雷也做出了相类似的成果。他运用类似的方法，构建了一批新函数L，从它们的解析特性中，得到了这样的结果：若l与k为互素的正整数，则算术级数l，l+k，l+2k……中一定有无限多个素数。

在欧拉和狄利克雷为解析数论打好基础以后，1859年，有一个人发表了一篇文章，正式宣告解析数论的创立。

这个人，就是黎曼。

在这篇论文中，他把欧拉恒等式的右边记作，并将其看做复变数。他认为，素数的性质可以通过复变函数来探讨，如素数的分布研究关键是研究复变函数的零点性质。而现在依旧没有解决的“黎曼猜想”，就是对复变函数零点性质的一个猜想——所有的复零点都在直线Re s=1/2上。

黎曼的论文，让解析数论开始了迅猛的发展。1896年，阿达马和瓦莱普桑，根据黎曼的方法与结果，应用整函数理论，成功地证明了素数定理，让解析数论成为了二十世纪最活跃的数论分支之一。

整函数，即在整个复平面上处处解析的函数。

解析数论在中国的发展也是极为迅猛。从最早的杨武之先生，到后来的华罗庚先生，王元先生以及陈景润先生，都在解析数论上有非常卓越的贡献。单讲陈景润先生，他对于{1，2}的证明，就是运用解析数论的方法来完成的，是目前世界上最好的证明结果。

解析数论的创立，让很多初等数论中很难证明的定理变得简单，同时可以提出更多新的数论问题，让数论这门学科的生命力得以延续。

好了，这就是有关数论历史的大体轮廓了。不得不说，想在短短的一篇推送里塞下整个数论的历史，简直就是痴心妄想……（然而还是做到……了？）

不过数论本身还是很精彩的，套用一句高斯的话：“如果说数学是科学的女皇，那么数论就是数学中的女皇”。大家不妨花点心思，来领略一下数论女皇的绝美身姿吧！

注：

数论是纯粹数学的分支之一，主要研究整数的性质。整数可以是方程式的解（丢番图方程）。有些解析函数（像黎曼ζ函数）中包括了一些整数、质数的性质，透过这些函数也可以了解一些数论的问题。透过数论也可以建立实数和有理数之间的关系，并且用有理数来逼近实数（丢番图逼近）。

按研究方法来看，数论大致可分为初等数论和高等数论。初等数论是用初等方法研究的数论，它的研究方法本质上说，就是利用整数环的整除性质，主要包括整除理论、同余理论、连分数理论。高等数论则包括了更为深刻的数学研究工具。它大致包括代数数论、解析数论、计算数论等等。

解析数论

借助微积分及复分析（即复变函数）来研究关于整数的问题，主要又可以分为乘性数论与加性数论两类。乘性数论藉由研究积性生成函数的性质来探讨素数分布的问题，其中质数定理与狄利克雷定理为这个领域中最著名的古典成果。加性数论则是研究整数的加法分解之可能性与表示的问题，华林问题是该领域最著名的课题。

解析数论的创立当归功于黎曼。他发现了黎曼zeta函数之解析性质与数论中的素数分布问题存在深刻联系。确切的说， 黎曼ζ函数的非平凡零点的分布情况决定了素数的很多性质。黎曼猜测， 那些零点都落在复平面上实部为1/2的直线上。这就是著名的黎曼假设—千禧年大奖难题之一。值得注意的是， 欧拉实际上在处理素数无限问题时也用到了解析方法。

解析数论方法除了圆法、筛法等等之外， 也包括和椭圆曲线相关的模形式理论等等。此后又发展到自守形式理论，从而和表示论联系起来。

代数数论

代数数论，将整数环的数论性质研究扩展到了更一般的整环上，特别是代数数域。一个主要课题就是关于代数整数的研究，目标是为了更一般地解决不定方程求解的问题。其中一个主要的历史动力来自于寻找费马大定理的证明。

代数数论更倾向于从代数结构角度去研究各类整环的性质， 比如在给定整环上是否存在算术基本定理等等。

这个领域与代数几何之间的关联尤其紧密， 它实际上也构成了交换代数理论的一部分。它也包括了其他深刻内容，比如表示论、p-adic理论等等。

几何数论

主要在于通过几何观点研究整数（在此即格点， 也称整点）的分布情形。最著名的定理为Minkowski定理。这门理论也是有闵科夫斯基所创。对于研究二次型理论有着重要作用。

计算数论

借助电脑的算法帮助研究数论的问题，例如素数测试和因数分解等和密码学息息相关的课题。

超越数论

研究数的超越性，其中对于欧拉常数与特定的riemann ζ函数值之研究尤其令人感到兴趣。此外它也探讨了数的丢番图逼近理论。

组合数论

利用组合和机率的技巧，非构造性地证明某些无法用初等方式处理的复杂结论。这是由保罗·艾狄胥开创的思路。比如兰伯特猜想的简化证明。

算术代数几何

这是数论发展到目前为止最深刻最前沿的领域， 可谓集大成者。它从代数几何的观点出发，通过深刻的数学工具去研究数论的性质。比如怀尔斯证明费马猜想就是这方面的经典实例。整个证明几乎用到了当时所有最深刻的理论工具。

当代数论的一个重要的研究指导纲领，就是著名的郎兰兹纲领。

∑编辑:Gemini

来源：数学建模

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域
稿件一经采用，我们将奉上稿酬。

投稿邮箱：[email protected]