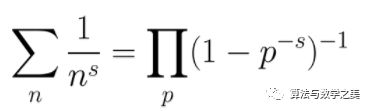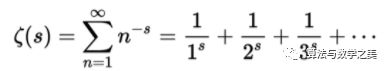被证明的黎曼猜想跟区块链加密算法有什么关系?
近日,一则发于外媒,随后被国内媒体大为传播的消息在数学界炸开了锅:黎曼猜想被证明了。而区块链届跟着躁动,加密算法要被破解了。
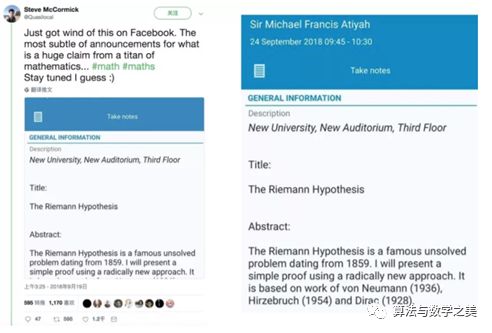
菲尔兹奖和阿贝尔奖双料得主、英国皇家学会前主席迈克尔· 阿提亚(Michael Atiyah,1929.4.22-)爵士宣称自己证明了黎曼猜想,并将在9月24日海德堡获奖者论坛上宣讲。据了解,迈克尔· 阿提亚的主要研究领域是几何,被誉为当代最伟大的数学家之一。
Michael Atiyah(1924-)
黎曼猜想在数学界的地位不容置喙。1859年,其由数学家黎曼提出,是当今数学界最重要、最期待解决的数学难题,至今已困扰人类一个半世纪。
黎曼猜想是什么?
质数是大于1的自然数中,除了1和自身之外,不能被其他自然数整除的数,例如2、3、5等。数学家早已证明质数有无穷多个,但这些质数在数轴上的分布遵循什么规律,或者是否真的存在一个精确的规律?
黎曼把欧拉提出的一个跟质数分布相关的函数zeta 函数,拓展到了适用于整个复平面。他猜测,这个拓展后的黎曼zeta函数,所有非平凡零点都位于实部等于1/2 的直线上。
大牛卢昌海这么说的(精简版本):
粗略地说, 它是针对一个被称为黎曼 zeta(ζ)函数的复变量函数 (即变量与函数值都可以在复数域中取值的函数) 的猜想。 黎曼 ζ 函数跟许多其它函数一样,在某些点上的取值为零, 那些点被称为黎曼 ζ 函数的零点。 在那些零点中, 有一部分特别重要的被称为黎曼 ζ 函数的非平凡零点。 黎曼猜想所猜测的是那些非平凡零点全都分布在一条被称为“临界线” 的特殊直线上。
详细版本:
早在1737年,大数学家欧拉就发现了质数分布问题与Zeta函数的联系,给出并证明了欧拉乘积公式,使得Zeta函数成为研究质数问题的经典方法。
欧拉乘积公式,其中p为质数,n为自然数
黎曼猜想(RiemannHypothesis)由大数学家黎曼在1859年首次提出,讨论黎曼Zeta函数的非平凡解问题。
黎曼猜想是关于黎曼Zeta函数的零点分布的猜想。黎曼Zeta函数长这个样子:
黎曼Zeta函数有两种零点,一种是位于实数轴线上的零点,被称为平凡零点,另一种是位于其他复平面区域上的零点,被称为非平凡零点,目前数学家已经证明这些非平凡零点全部位于实部区间为0到1的复平面内,而黎曼则大胆猜想,这些非平凡零点全部位于实部为1/2的一条直线上。这就是黎曼猜想!
有关黎曼猜想的更多内容,请转阅:
黎曼猜想证明新进展
素数之魂——黎曼和他的伟大猜想
黎曼猜想和哥德巴赫猜想有什么联系?
世界七大数学难题与Hilbert的23个问题
截至目前,数学论文中的研究,其中很多数学命题都是以黎曼猜想及推广形式的成立作为前提。如果黎曼猜想被证实或证明,这些数学命题将荣升为数学定理;而如果一旦被证伪,则代表将有千余个数学命题不被成立。
所以,基于这一研究意义,数学界对于迈克尔· 阿提亚9月24日的宣讲自然格外在意。而除了研究意义外,黎曼猜想因为能揭示素数分布的统计规律,跟需要用到素数的加密算法有一定联系,也触发了一些区块链自媒体和币圈人士的“G”点。
查阅资料了解到,一直以来,素数的分布很难捕捉到规律,黎曼在其论文中指出素数的分布完全蕴藏在一个特殊的函数中(黎曼函数),这也构成了黎曼猜想关于素数的分布。而目前区块链领域用到的加密算法,和素数的分布轨迹有一定联系。
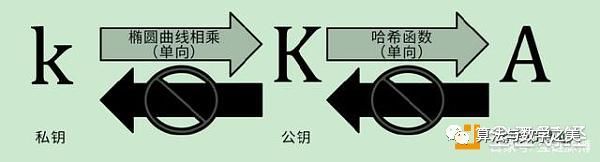
在一些人看来,如果黎曼猜想被证明,其或有可能影响加密算法的逻辑性,比如加密算法和哈希函数如何产生互动等,甚而破解加密算法,从而上升至对加密货币圈产生影响。
针对这一议题,随即采访了几位关注加密算法和密码学的专家老师。依据他们的观点,大致可总结为:就算黎曼猜想被证明,也没区块链加密算法什么事。
一位某知名科技媒体从业者告诉,从理论角度看,“需要用到素数的加密算法”基本就是RSA了。RSA虽然在普通工业加密中有一些应用,如比特币使用的是专门经过修改的椭圆曲线加密。而其他虚拟货币使用的加密算法,几乎很少会使用RSA,所以和黎曼猜想没多大关系。
而从应用角度来看,“黎曼猜想的命题是完整的,只要认为它为真就可以拿来用,而不需要一定等到‘证明了为真’才可以用。而且,从来没听说过针对任何领域的任何攻击方法里,黎曼定理起到了重要作用。”
另一位公链开发共识算法工程师则表示,对于大多数区块链技术而言,使用的哈希算法和素数没有关系,使用的非对称算法是ECC,ECC是基于椭圆曲线上的离散对数问题,和素数也没有关系。
“退一步讲,如果非要说有关系,我想可能也就一个做‘质数币’的项目。该项目的工作是把比特币的挖矿算法修改为寻找质数,没有其他的特别之处。所以也就币圈有人在炒,”该名人士向表示,“黎曼猜想可能会对质数的预测有影响,但在黎曼猜想被证明之前,大家就对这个猜想的内容是认同的,所以依然可以用它来寻找质数。”
综合来看,这两位人士所持意见一致。即黎曼猜想被证明,更多的是对数学学科的贡献。若是在工程领域,除非黎曼猜想被证伪,不然影响都不会很大!
那么,黎曼猜想的影响到底何在?
当然, 黎曼猜想确实是非常艰深的, 它自问世以来, 已经有一个半世纪以上的历史。 在这期间, 许多知名数学家付出了艰辛的努力,试图解决它, 却迄今没有人能够如愿。 但是, 如果仅仅用艰深来衡量的话, 那么其它一些著名数学猜想也并不逊色。 比如费尔玛猜想是经过三个半世纪以上的努力才被证明的;哥德巴赫猜想则比黎曼猜想早了一个多世纪就问世了, 却跟黎曼猜想一样迄今屹立不倒。 这些纪录无疑也都代表着艰深!
那么, 黎曼猜想被称为最重要的数学猜想, 究竟是什么原因呢?
首要的原因是它跟其它数学命题之间有着千丝万缕的联系。据统计, 在今天的数学文献中已经有一千条以上的数学命题是以黎曼猜想 (或其推广形式) 的成立为前提的。 这表明黎曼猜想及其推广形式一旦被证明, 对数学的影响将是十分巨大的, 所有那一千多条数学命题就全都可以荣升为定理;反之, 如果黎曼猜想被推翻, 则那一千多条数学命题中也几乎无可避免地会有一部分成为陪葬。 一个数学猜想与为数如此众多的数学命题有着密切关联, 这在数学中可以说是绝无仅有的。
其次, 黎曼猜想与数论中的素数分布问题有着密切关系。 而数论是数学中一个极重要的传统分支,被德国数学家高斯称为是 “数学的皇后”。 素数分布问题则又是数论中极重要的传统课题, 一向吸引着众多数学家的兴趣。 这种深植于传统的 “高贵血统” 也在一定程度上增加了黎曼猜想在数学家们心中的地位和重要性。
再者, 一个数学猜想的重要性还有一个衡量标准, 那就是在研究该猜想的过程中能否产生出一些对数学的其它方面有贡献的结果。用这个标准来衡量, 黎曼猜想也是极其重要的。 事实上, 数学家们在研究黎曼猜想的过程中所取得的早期成果之一,就直接导致了有关素数分布的一个重要命题——素数定理——的证明。 而素数定理在被证明之前, 本身也是一个有着一百多年历史的重要猜想。
最后, 并且最出人意料的, 是黎曼猜想的重要性甚至越出了纯数学的范围,而 “侵入” 到了物理学的领地上。 20 世纪 70 年代初, 人们发现与黎曼猜想有关的某些研究, 居然跟某些非常复杂的物理现象有着显著关联。 这种关联的原因直到今天也还是一个谜。但它的存在本身, 无疑就进一步增加了黎曼猜想的重要性。
有这许多原因, 黎曼猜想被称为最重要的数学猜想是当之无愧的。
∑编辑 | Gemini
来源 | 整理自网络
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域,经采用我们将奉上稿酬。
投稿邮箱:[email protected]