联合熵(joined entropy)、条件熵(conditional entropy)、相对熵(relative entropy)、互信息(mutual information)以及相关关系整理
这部分内容算是对前面时间序列中近似熵、样本熵、模糊熵等熵的基础部分,毕竟前面部分只是对各种熵的求法步骤做了归纳,要理解其中的意义来得从最基础的部分进行分析。
Entropy (熵)
熵是衡量随机变量不确定性的指标。根据Shannon的定义,对于一个在概率空间 Ω \Omega Ω 中,具有概率分布 p ( x ) p(x) p(x) 的随机变量 X X X,它的熵的定义为:
H ( X ) c o n t i n u o u s = − ∫ Ω p ( x ) l o g 2 ( p ( x ) ) d x H(X)continuous = -\int_{\Omega}p(x)log_{2}(p(x))dx H(X)continuous=−∫Ωp(x)log2(p(x))dx H ( X ) d i s c r e t e = − ∑ x ∈ Ω p ( x ) l o g 2 ( p ( x ) ) H(X)discrete = -\sum_{x\in\Omega}p(x)log_{2}(p(x)) H(X)discrete=−x∈Ω∑p(x)log2(p(x))其中,上面两个式子分别是当 X X X 为连续或者离散随机变量时,所以 p ( x ) p(x) p(x) 也便是对应的连续概率分布或者离散概率分布。
由于连续的情况是基于离散情况泛化出的结果,所以下面以离散随机变量的情况为例分析。
举个扔硬币的例子,一个硬币正反两面的概率都是 1 2 \frac{1}{2} 21,所以对于正负结果这个随机变量,它的熵为: H ( x ) = − 1 2 l o g 2 ( 1 2 ) − 1 2 l o g 2 ( 1 2 ) = 1 H(x)=-\frac{1}{2}log_{2}(\frac{1}{2})-\frac{1}{2}log_{2}(\frac{1}{2})=1 H(x)=−21log2(21)−21log2(21)=1再举个极端的例子,这个硬币每次扔都是正面或者背面向上,此时的熵为: H ( x ) = − 1 l o g 2 ( 1 ) = 0 H(x)=-1log_{2}(1)=0 H(x)=−1log2(1)=0对于这样具有两个状态空间的变量,当概率分布变化时,得到的熵的变化对应如下:
图中可以看出,当概率为 1 2 \frac{1}{2} 21时熵最大。对于不确定性,也可以理解对于一个问题有不同的答案,像扔硬币这个例子,问题就是结果是正面还是背面,当极端情况下只有背面或者正面的结果时,问题的答案就没有任何疑问,此时也便不具有不确定性,所以熵为0;当概率五五开时,此时问题的答案就有不确定性,并且此时的不确定性是最大的。
熵是有界的,下面的不等式适用于离散随机变量: 0 ⩽ H ( X ) ⩽ l o g 2 ( ∣ X ∣ ) 0 \leqslant H(X) \leqslant log_{2}(|X|) 0⩽H(X)⩽log2(∣X∣)其中, ∣ X ∣ |X| ∣X∣ 表示离散变量 X X X 的值的个数,其中当 X X X 服从于均匀分布 (uniform distribution) 时等号成立。
Joined Entropy (联合熵)
对于两个离散随机变量 X , Y X, Y X,Y,则它们的联合熵是: H ( X , Y ) = − ∑ x ∈ X y ∈ Y p ( x , y ) l o g 2 ( p ( x , y ) ) H(X, Y)=-\sum_{x\in X y\in Y}p(x,y)log_{2}(p(x,y)) H(X,Y)=−x∈Xy∈Y∑p(x,y)log2(p(x,y))联合熵可以归纳到多变量的情况下,对于 X 1 , . . . , X n X_{1},...,X_{n} X1,...,Xn 有 H ( X 1 , . . . , X n ) H(X_{1},...,X_{n}) H(X1,...,Xn)。
Conditional Entropy (条件熵)
条件熵的表现形式是: H ( X ∣ Y ) = − ∑ x ∈ X , y ∈ Y p ( x ∣ y ) l o g 2 ( p ( x ∣ y ) ) H(X|Y)=-\sum_{x\in X, y\in Y}p(x|y)log_{2}(p(x|y)) H(X∣Y)=−x∈X,y∈Y∑p(x∣y)log2(p(x∣y))当 X , Y X,Y X,Y 是对立的随机变量时,条件熵的表现形式是: H ( X ∣ Y ) = − ∑ x ∈ X , y ∈ Y p ( x ) l o g 2 ( p ( x ) ) = H ( X ) H(X|Y)=-\sum_{x\in X, y\in Y}p(x)log_{2}(p(x))=H(X) H(X∣Y)=−x∈X,y∈Y∑p(x)log2(p(x))=H(X)条件熵和联合熵之间的关系是: H ( X , Y ) = H ( X ) + H ( Y ∣ X ) = H ( Y ) + H ( X ∣ Y ) H(X, Y) = H(X) + H(Y|X) = H(Y) + H(X|Y) H(X,Y)=H(X)+H(Y∣X)=H(Y)+H(X∣Y)
Relative Entropy (相对熵)
相对熵也称作K-L散度 (Kullback–Leibler divergence),K-L距离 (Kullback–Leibler distance)。是用来衡量两个随机变量的概率分布之间的差异性的指标。
还是以随机变量 X , Y X,Y X,Y为例,它们对应的概率分布分别是 p ( x ) , q ( y ) p(x), q(y) p(x),q(y),当 X , Y X,Y X,Y为离散型变量时, p p p对 q q q的相对熵为: D ( p ∣ ∣ q ) = ∑ x ∈ X , y ∈ Y p ( x ) l o g 2 p ( x ) q ( x ) D(p||q) = \sum_{x\in X,y\in Y} p(x)log_{2}\frac{p(x)}{q(x)} D(p∣∣q)=x∈X,y∈Y∑p(x)log2q(x)p(x)当 X , Y X,Y X,Y为连续型变量时, p p p对 q q q的相对熵为: D ( p ∣ ∣ q ) = ∫ x ∈ X , y ∈ Y p ( x ) l o g 2 p ( x ) q ( x ) d x D(p||q) = \int_{x\in X,y\in Y} p(x)log_{2}\frac{p(x)}{q(x)}dx D(p∣∣q)=∫x∈X,y∈Yp(x)log2q(x)p(x)dx当 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)的相似度越高,相对熵越小。
KL散度主要有两个性质:
(1)、不对称性
尽管KL散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即 D ( P ∣ ∣ Q ) ! = D ( Q ∣ ∣ P ) D(P||Q)!=D(Q||P) D(P∣∣Q)!=D(Q∣∣P)。
(2)、非负性
相对熵的值是非负值,即 D ( P ∣ ∣ Q ) > 0 D(P||Q)>0 D(P∣∣Q)>0。
Mutual Information (互信息)
对于两个随机变量 X , Y X,Y X,Y,它们的互信息可以定义为 X , Y X,Y X,Y的联合分布和对立分布乘积的相对熵。 I ( X ; Y ) = D ( p ( x , y ) ∣ ∣ p ( x ) q ( y ) ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) l o g 2 p ( x , y ) p ( x ) p ( y ) I(X;Y)=D(p(x,y)||p(x)q(y))=-\sum_{x\in X,y\in Y} p(x,y)log_{2}\frac{p(x,y)}{p(x)p(y)} I(X;Y)=D(p(x,y)∣∣p(x)q(y))=−x∈X,y∈Y∑p(x,y)log2p(x)p(y)p(x,y)经过变形和计算可以得到互信息 I ( X ; Y ) = H ( X ) + H ( Y ) − H ( X , Y ) I(X;Y)=H(X)+H(Y)-H(X,Y) I(X;Y)=H(X)+H(Y)−H(X,Y)
互信息的意义是衡量 X X X到 Y Y Y的不确定性的减少程度,另外互信息是对称的(symmetric),也就是 I ( X ; Y ) = I ( Y ; X ) I(X;Y) = I(Y;X) I(X;Y)=I(Y;X),所以互信息不能用于确定信息流的方向。
总结
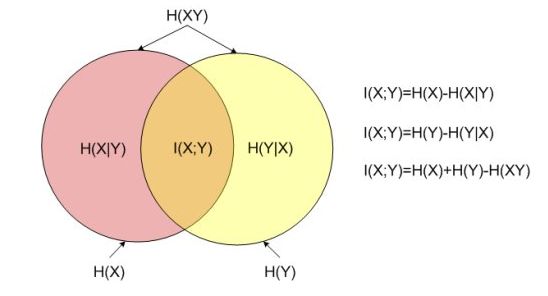
对于随机变量 X , Y X,Y X,Y,它们的熵、联合熵、条件熵以及互信息之间的关系是:
其中,左边的圆形区域表示随机变量 X X X的熵,右边的圆形区域表示随机变量 Y Y Y的熵。左边的 H ( X ∣ Y ) H(X|Y) H(X∣Y)区域表示在随机变量 Y Y Y给定的条件下随机变量 X X X的条件熵;左边的 H ( Y ∣ X ) H(Y|X) H(Y∣X)区域表示在随机变量 X X X给定的条件下随机变量 Y Y Y的条件熵。两个圆中间相交的部分表示随机变量 X , Y X,Y X,Y的互信息。两个圆构成的整体部分表示 X , Y X,Y X,Y的联合熵。
REF
《Entropy Analysis of Financial Time Series》
信息熵,条件熵,互信息的通俗理解
详解熵、最大熵、联合熵和条件熵、相对熵以及互信息之间的关系