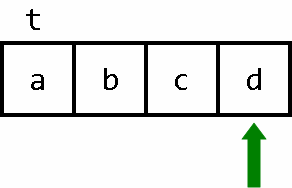Brainf**k 程序设计

前一段时间听说了一门叫做“brainfuck”的编程语言，感觉很是神奇，就打算抽时间研究一套用这门语言做程序设计的方法。虽说纯属娱乐，但是还是感觉收获颇丰。

下文内容中，所有

引用内容

都会标明出处。其余绝大多数内容均来自个人“创意（YY）”，如有雷同纯属巧合。由于笔者水平有限，内容中如有不妥，请在评论区评论，我会尽快更正。

---

What is Brainf**k ?

Brainfuck是一种极小化的计算机语言，它是由Urban Müller在1993年创建的。由于fuck在英语中是脏话，这种语言有时被称为brainf*ck或brainf**k，甚至被简称为BF。 ——百度百科

同学们可能都听说过“汇编语言”，汇编语言可谓是高级语言的鼻祖（其实应该说是先驱）。可是，就连 8086汇编语言 中的常用功能都有近百种，更何况是高级语言。但是 Brainf**k 语言却十分惊人，只有区区8种指令。在这种语言的源代码中，一个字符代表一条指令，而不是像其他语言一样用类似英文单词的助记符代表指令。

程序运行时，你会被赋予一个长度（可以认为是）无限长的一维储存空间，这个储存空间可以被视为一个字符数组。你有一个指针，最开始的时候指向数组首部。程序运行时，会根据指令调整这个指针的位置，同时也可以修改指针所指向的那个储存单元中的数值。

（图灵机？因为与下文内容关联不大，在此不与介绍。）

这八种功能（状态）如下：

字符	含义
>	指针 向右移动 一个位置
<	指针 向左移动 一个位置
+	指针指向的字节 储存的值 加一
-	指针指向的字节 储存的值 减一
.	以字符的形式 输出指针指向的字节
,	从键盘输入一个字符 并将其 储存在 指针指向的位置
[	判断指针指向的位置中 储存的信息 是否为零。如果为零，则程序跳转到与该 “[” 匹配的 “]” 的下一条指令继续执行。否则不进行跳转，直接执行下一条指令。
]	判断指针指向的位置中 储存的信息 是否非零。如果非零，则程序跳转到与该 “]” 匹配的 “[” 的下一条指令继续执行。否则不进行跳转，直接执行下一条指令。

这些描述可能不是很好理解，百度上给出了一个非常形象的解释：

Brainfuck程序可以用下面的替换方法翻译成C语言(假设ptr是char*类型):

字符	含义
>	++ptr;
<	--ptr;
+	++*ptr;
-	--*ptr;
.	putchar(*ptr);
,	*ptr =getch();
[	while (*ptr) {
]	}

不难看出左中括号和右中括号构成了一个while循环。

感兴趣的同学可以到这个网站上去运行自己写的Brainf**k程序。

http://fatiherikli.github.io/brainfuck-visualizer/

但是由于这个可视化解释器运行速度太慢（即使调到最快，我还是觉得不够快），再加上可视储存空间太少，所以我就自己写了一个相当简陋的Brainf**k解释器（懒得做可视化…），代码也很简单：

#include 
#include 
#include 

#include 
#include 
#include 
#include 
using namespace std;

#define MaxSize (10000000 + 8)
char sseg[MaxSize], cseg[MaxSize]; /// 堆栈段 代码段 
int mtch[MaxSize]; /// 记录中括号匹配位置(不必清空) 
int sptr = 0, cptr = 0; /// 伪指针 

stack<int> Lpos; /// 用栈记录左中括号的出现位置 
int run(int spos = -1, int cpos = -1) { /// 运行代码段中的程序 
    if(spos >= 0) sptr = spos;
    if(cpos >= 0) cptr = cpos; /// 指针初始位置 
    for(int i = 0; cseg[i]!=0 && cseg[i]!=EOF; i ++) { /// 中括号匹配 
        char& ope = cseg[i];
        if(ope == '[') {
            mtch[i] = -1; /// 为匹配的左中括号
            Lpos.push(i); 
        } else if(ope == ']') {
            if(Lpos.empty()) {
                printf("--- \']\' without \'[\' has been found ...\n");
                return 2;
            }
            int Lnow = Lpos.top(); Lpos.pop();
            mtch[Lnow] = i;
            mtch[i] = Lnow;
        }
    }
    if(Lpos.size() != 0) {
        while(Lpos.size()) Lpos.pop(); /// 弹空 
        printf("--- \'[\' without \']\' has been found ...\n");
        return 3; 
    }
    //printf("--- match suceeded, running ...\n");
    //for(int i = 0; i <= 50; i ++) {
    //    printf("%3d: %c %5d\n", i, cseg[i], mtch[i]);
    //}
    //system("pause");
    while(cseg[cptr]!=0 && cseg[cptr]!=EOF) {
        //system("cls"); 简陋的“可视化”...(其实我很讨厌这种做法...)
        //printf("--- cptr = %7d (%7d):\n", cptr, mtch[cptr]);
        char& ope = cseg[cptr];
        switch(ope) { /// 检测操作符 
            case '<':
                sptr --; cptr ++; break;
            case '>':
                sptr ++; cptr ++; break;
            case '+':
                if(sptr < 0) {
                    printf("--- stack error: operator on illegal pos ...\n");
                    return 1;
                }
                sseg[sptr] ++; cptr ++; break;
            case '-':
                if(sptr < 0) {
                    printf("--- stack error: operator on illegal pos ...\n");
                    return 1;
                }
                sseg[sptr] --; cptr ++; break;
            case '.':
                putchar(sseg[sptr]); cptr ++; break;
            case ',':
                sseg[sptr] = getch(); cptr ++; break;
            case '[':
                if(sptr < 0) {
                    printf("--- stack error: operator on illegal pos when at \'[\'...\n");
                    return 4;
                }
                if(sseg[sptr] == 0) {
                    cptr = mtch[cptr] + 1;
                }else {
                    cptr ++;
                }
                break;
            case ']':
                if(sptr < 0) {
                    printf("--- stack error: operator on illegal pos when at \']\'...\n");
                    return 4;
                }
                if(sseg[sptr] != 0) {
                    cptr = mtch[cptr] + 1;
                }else {
                    cptr ++;
                }
                break;
            default: cptr ++;
        }
        //for(int i = 0; i <= 18; i ++) {
        //    printf("%4d", i);
        //}
        //putchar('\n');
        //for(int i = 0; i <= 18; i ++) {
        //    printf("%4d", sseg[i]);
        //}
        //putchar('\n'); putchar('\n');
    }
}

void readfile(const char* filepath) { /// 读入文件 
    FILE* fpin = fopen(filepath, "r");
    char cn = 0; int i = 0;
    do {
        cn = fgetc(fpin);
        cseg[i ++] = cn;
    }while(cn != EOF);
    printf("--- readfile succeeded \"%s\" ...\n", filepath);
    fclose(fpin);
}

void show(int L = 0) {
    for(int i = L; i < L + 18; i ++) printf("%4d", i);
    putchar('\n');
    for(int i = L; i < L + 18; i ++) printf("%4d", (unsigned char)sseg[i]);
    putchar('\n');
    for(int i = L; i < L + 18; i ++) {
        if(i == sptr) {
            printf("  △");
        }else printf("    ");
    }
    putchar('\n');
}

int main() {
    printf("--- this is a brainf**k interpreter, Made by GGN 2019.1.18 \n");
    readfile("main.brfk");
    //sseg[0] = 1; sseg[1] = 0;
    //sptr = 1;
    show(); 
    run();
    show();
    return 0;
}

（把所有Tab换成四个空格真的好累啊，给CSDN的代码片功能差评…）

借助这个简陋解释器，我们就可以初步开始我们的程序设计尝试了。

---

笔者：关于Brainf**k程序设计的一些看法

其实大家也都明白，Brainf**k这门语言并不是很适合程序设计，但是它却十分能培养人的算法思维。在学习高级语言的过程中，你不必思考那么多成型的函数、方法在底层都是如何去实现的，但是在Brainf**k面前“樯橹灰飞烟灭”。这个时候，你必须严密的逻辑思维能力，才能完成那些在高级语言中看起来“很简单”、“很显然”的任务。

所以说我个人认为，Brainf**k程序设计时应关注以下问题：

1. 成体系的编程理念，以及详细的注释，大力提高 代码的可读性。
2. 在具有代码可读性的前提下，应尽可能追求 编写的简洁
3. 适当的时候，还应该考虑一下程序的 运行效率

这与 用高级语言 编写程序时的 编写理念 或许 存在着一定的差距。（也正是因为这一点，我不打算从“HelloWorld”开始探讨这门语言。很多人都是因为看了网上给出的“HelloWorld”程序就望而却步的。）

另外，如果时间允许的话，我打算写一个简陋的（不合规矩）的编译器，试图把一门类似高级语言的编程语言（之所以说是类似，是因为我认为这门语言可能无法实现函数的递归，或者说无法实现一个正常高级语言意义下的函数。）编译成Brainf**k。不过在这之前，我可能需要先设计一门中间语言，来降低一下工作难度（毕竟我这个人是个ZZ…）。

再说一些题外话，我个人认为我们还可以 以brainf**k这门语言为背景来 开发编程类游戏，或者举办与之相关的创意程序设计比赛…总之一句话，我觉得这门编程语言有一定的 发展前景。

---

第一章 - BYTE类型的基础运算方法

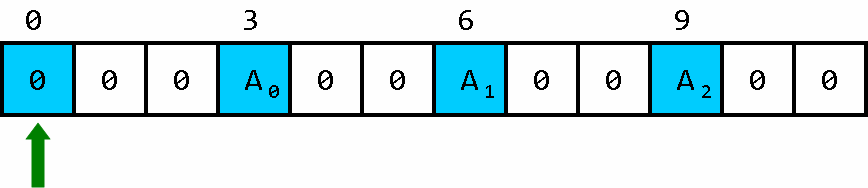
在本章中我会用如下的方式，描述当前线性空间的“状态”：

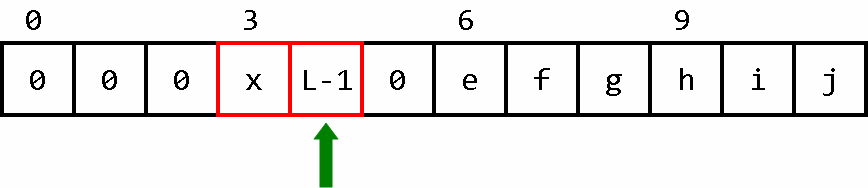
上图中：a、b、c、d表示储存单元中储存的信息（unsigned char类型，值域[0,255]）。“绿色箭头”表示 当前 指针指向的 储存单元。t 表示：信息 a 所在的储存单元标号为 t，信息 b 所在的储存单元标号为 t+1（由于储存空间是无限长的，图片只能展现整个线性空间的一部分。所以，那些在当前程序过程中没有“涉及到”的储存单元，在图片中会被省略。另外，t 从 0开始计数） …

操作(-2)：清空当前BYTE

（红色箭头左侧表示程序段进行前的状态，右侧表示程序段进行后的状态。其中a表示该储存单元中储存着一个不确定的值，0表示该储存单元中的值必须为零。）

实现原理很简单，如果当前储存单元非零，就循环减一即可。

[-] 清零

不要小瞧这个简单的程序段，它很有用的！

操作(-1)：BYTE的移动

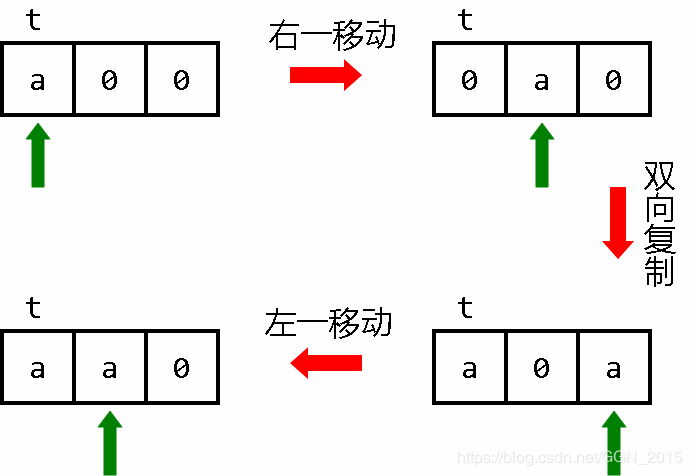
移动，就是把一个数据从一个储存单元转移到另一个储存单元。移动之后，原来的储存单元中的值会变成零。（因为与传统的数据“传送”不同，称为移动加以区分，其实名字都是我自己编的，如有不妥敬请谅解。）

原理很简单，利用循环让两个储存单元，一个连续减一，一个连续加一，即可。

图片中所展示的 这种 从做向右的转移 我们暂且称之为“右一移动”（因为它把数据向右移动到了下一个位置），同理还有“左一移动”、“右n移动”、“左n移动”（n为常数）等等。（名字是编的，主要是为了后文交流方便。）

[->+<]>        右一移动

[-<+>]<        左一移动

移动功能的主要用途是实现传送。

操作0：BYTE的传送

传送和转移方法类似，只不过是在复制数据时不销毁原有数据，传送的实现方法有很多，在此只介绍一种方法（效率并不是很高，不过还说得过去）。

“诶，博主？你的图片是不是搞错了，为什么后面多画了一个存着零的储存单元？”

并不是博主的图片错了，而是因为我们在运算过程中需要用到这个储存单元，如果这个储存单元原有的值不是零，那么我们的运算就会出错！

上图向你详细地展示了右一传送的实现过程：

右一传送:
[->+<]>      右一移动
[-<+>>+<]>   双向复制
[-<+>]<      左一移动

如果你要是不相信笔者代码的正确性，你可以把这个代码粘贴到Brainf**k在线可视化解释器上运行一下：

+++++   把零号储存单元设置成5

右一传送:
[->+<]>      右一移动
[-<+>>+<]>   双向复制
[-<+>]<      左一移动

同理还有“右n传送”，“左n传送”，必要的时候需要注意储存单元内容的清零。

上文中的储存单元 t+2 就是一个典型的辅助运算单元。它的位置不一定在 t+2，但是必须保证运算前，里面存储的值为0。这种 利用辅助运算单元进行计算的方法 在后文中 有着很多的应用。

传送的用处很多，可以说是BYTE数值运算的基础。我们经常用传送把数据转移到运算栈的栈顶。（大多数时候，整个线性储存空间，就被视为是我们的运算栈。）

操作1：BYTE的交换

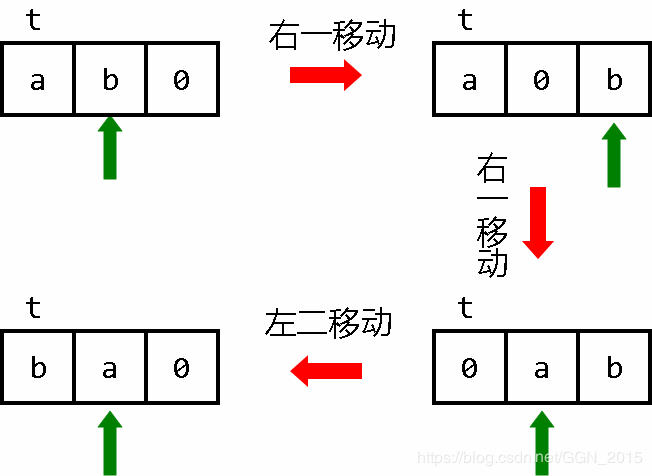
很简单，两次传送即可，需要一个辅助运算单元。在此我们只介绍“临位交换”的一种很无脑的方法。

三次数据移动，必要的时候记得修改指针的位置：

临位交换:
[->+<]>      右一移动 b
<<           指针回到 a
[->+<]>      右一移动 a
>            指针回到 b
[-<<+>>]<<   左二移动 b
>            指针回到 a

不难发现，代码中有一些可以压缩的冗余运算，不过为了思路清晰，我不建议删掉这些冗余运算（主要是因为我ZZ）。

你可以在可视化解释器上试一试这个程序：

+++++ 把零号单元的值设置成5
>
+++   把一号单元的值设置成3

临位交换:
[->+<]>      右一移动 b
<<           指针回到 a
[->+<]>      右一移动 a
>            指针回到 b
[-<<+>>]<<   左二移动 b
>            指针回到 a

操作2：BYTE相加

不难发现，数据的移动本质上就是一个累加的过程。

试试这个：

+++++ 把零号单元的值设置成5
>
+++   把一号单元的值设置成3

BYTE相加:
[-<+>]<      左一移动

再试试这个：

+++++ +++++     +++++ +++++     +++++ +++++     +++++ +++++
+++++ +++++     +++++ +++++     +++++ +++++     +++++ +++++
+++++ +++++     +++++ +++++     +++++ +++++     +++++ +++++
+++++ +++++     +++++ +++++     +++++ +++++     +++++ +++++
+++++ +++++     +++++ +++++     +++++ +++++     +++++ +++++
+++++ +++++     +++++ +++++     +++++ +++++     +++++ +++++
+++++ +++++     +++++
    把零号单元的值设置成 255
>
+   把一号单元的值设置成 1

BYTE相加:
[-<+>]<      左一移动

第二个程序运行结束后，得到了0，这说明Brainf**k遵循二进制运算的溢出原则。

操作3：BYTE相乘

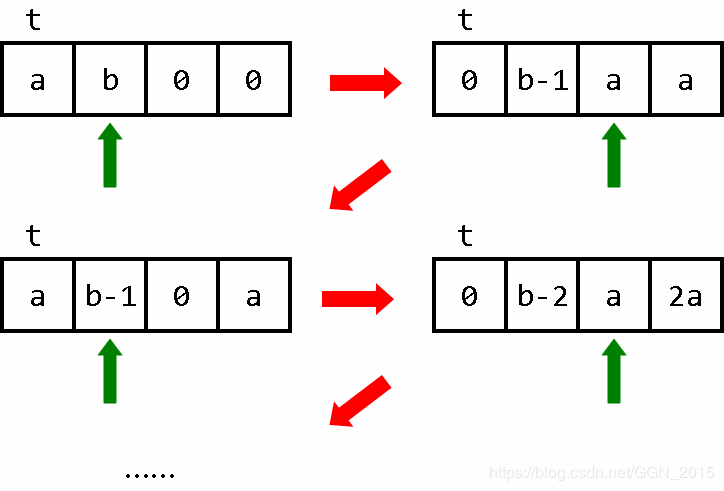
循环加即可，b 每一次减一时，都把 a 在累加器上累加一次。但要注意保护 a 的原始值不被破坏。

以b为循环变量，每次循环时b自减一，复制过去两个 a，移动回来一个即可。

+++++ 把零号单元的值设置成5
>
+++   把一号单元的值设置成3

BYTE相乘：
[    以 b 为循环变量 进行循环
  -               自减一
  <               指针指向 a
  [->>+>+<<<]>>   复制两个 a
  [-<<+>>]<<      左二移动
  >  因为 b 是循环变量 指针指回 b 
]
< [-]         a 位置清零
>>>           找到运算结果
[-<<<+>>>]<<< 左三移动

操作3.3：判断BYTE非零

BYTE非零计算结果为1，BYTE为零计算结果为0。

利用循环变量的性质即可实现——如果循环变量的值非零，那么我们就可以进入循环体。这时如果我们把循环变量的值清零，就能保证循环一定会立即退出。循环退出前，把右侧的辅助运算单元的值设置为1；循环退出后，对右侧的辅助运算单元进行左一移动即可。

+++++ 把零号单元的值设置成5

BYTE非零：
[
  [-]    循环变量清零
  >+<    右侧位置赋值为1
]
>          找到右侧位置
[-<+>]<    左一移动

这种方法可以用于判断两个数是否不相等。

操作3.6：判断BYTE为零

判断BYTE是否非零，然后取反即可。（什么？你不会取反？由于上一问的运算结果非0即1，用1减去上一问的运算结果即可。）

+++++ 把零号单元的值设置成5

BYTE为零：
[
  [-]    循环变量清零
  >+<    右侧位置赋值为1
]
+>          置一，并找到右侧位置
[-<->]<     用一减（你能看出它和 "左一移动" 的差别）

这种方法可以用来判断两个数是否相等。

操作3.9：关于 逻辑运算 与、或、非、异或

我们约定，对于一个变量，如果我们能确保，它的值要么是0，要么是1，那么我们就称这个变量为“布尔变量”。我们用1表示逻辑真值（True），用0表示逻辑假值（False）。不难得出以下结论

$$a\wedge b=a\times b$$

$$a\vee b=1-(1-a)\times (1-b)=sgn(a+b)$$

$$\neg a=1-a$$

注：

$$sgn(x)=\{\begin{array}{r}1,x>0\\ 0,x=0\\ -1,x<0\end{array}$$

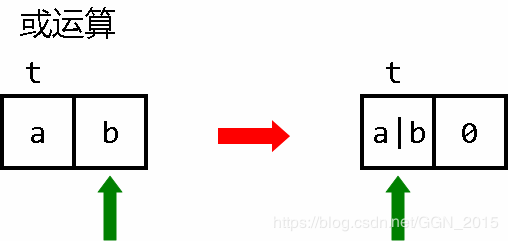
在此给出 或运算 和 非运算 的程序段。

或运算:
[-<+>]<     左一移动（求和）
[[-]>+<]>   判断非零
[-<+>]<     左一移动

非运算:
>+<      放置一
[->-<]>  右减左（其实就是在右一移动上稍加修改）
[-<+>]<  左一移动

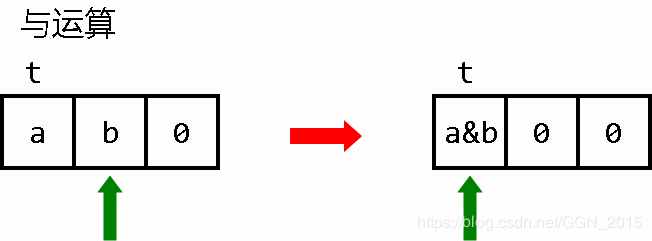
由于乘法需要两个辅助运算单元，如果单纯是做 与运算，其实只需要一个辅助运算单元就够了，这在一定程度上也可以看做是一种优化。

与运算:
<                  指针对准第一个数
[[-]>[[-]>+<]<]    如果两个数都非零，那么辅助运算单元会被赋值为1
[-]>[-]>           清空前两个位置的值
[-<<+>>]<<         左二移动

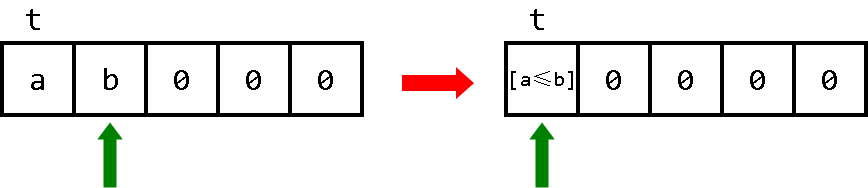
操作4：判断无符号BYTE x 小于等于 y

先“批判”一下我昨天想出来的（垃圾）判断方法：

原理很简单，两个数轮流减一，谁先减到0，谁就是较小数。

比较两个正数的大小关系
判断 x 小于等于 y

栈中内容 x 0 0 y 0 0 0
运算后   a

<<<<<< 移动到 x

右一传送
[>+<-]>    向右移动
[>+<<+>-]> 双向复制
[<+>-]<    向左移动

判等于零
[[-]>+<]  置一
+>[-<->]< 用一减

>> 移动到 y

右一传送
[>+<-]>    向右移动
[>+<<+>-]> 双向复制
[<+>-]<    向左移动

判等于零
[[-]>+<]  置一
+>[-<->]< 用一减

将两个判零运算结果求和
<<<
[->>>+<<<]
>>>

如果这个和不等于零 说明 x 和 y 已经有一个为零
判等于零

[[-]>+<]   置一
+>[-<->]<  用一减
[>+<-]>    向右移动
[>+<-]>    向右移动

上述运算结果表示 两者中是否不存在零

如果不存在零 则需要把两个数同时减一 直到出现零为止

大循环 循环减一
[[-]   记得清空上一次的循环标记
  <<<<<< - 移动到 x 并减一
  >>> -    移动到 y 并减一
  >>> 回到栈顶 并执行与前文相同的操作
  
  <<<<<< 移动到 x
  [>+<-]>    向右移动
  [>+<<+>-]> 双向复制
  [<+>-]<    向左移动
  [[-]>+<]   置一
  +>[-<->]<  用一减

  >> 移动到 y
  [>+<-]>    向右移动
  [>+<<+>-]> 双向复制
  [<+>-]<    向左移动
  [[-]>+<]   置一
  +>[-<->]<  用一减

  将两个判零运算结果求和
  <<<
  [->>>+<<<]
  >>>

  [[-]>+<]   置一
  +>[-<->]<  用一减
  [>+<-]>    向右移动
  [>+<-]>    向右移动

]

这时两个数中的较小数已经被减为零
判断 x 是否等于零 即可得出 x 是否是较小数

<<<<<< 移动到 x
[[-]>+<]   置一
+>[-<->]<  用一减

运算结果即为答案 但要记得清空 y 的值

>>>[-]<<<  清空 y

运算完成

采用这个思路，效率还比较可观（后期我们会专门做各种算法的效率分析），不过我后来对这个方法进行了小小的改良，所以在此不介绍这种方法。

由于这个程序相对复杂，我们可以先用高级语言（例如c++）编写一段伪代码，然后再用人脑编译成Brainf**k的方法实现。

给出一些基本的替换思路：

条件判断语句：

c++

if(exp) {
  operations;
}

brainf**k

push exp      （exp 进栈处理）
[[-]          （进入 if 并且将 exp 的值清零，清零是为了及时退出循环）
  operations  （要注意，所有操作结束时，指针要回到原栈顶，辅助运算单元要清零）
]

循环语句：

c++

while(exp) {
  operations;
}

brainf**k

push exp 
[[-]         （清空）
  operations （注意事项同上）
  push exp
]

仔细阅读，不难发现，前文的那个（垃圾）判断方法，就是用这种 while 循环的替换实现的。其中push exp占据了大篇幅，而operations却只有三行（就是让 x 和 y 都自减一的语句）。这种方法的“垃圾”之处，主要在于辅助运算单元太多，接下来我们可以压缩一下辅助运算单元的数量。另外，在push exp的时候也有很多可优化的细节。

c++ 伪代码

unsigned char x, y; // 比较 x 和 y 的大小（假设 x 和 y 的值会被预先放到内存中）
unsigned char a;    // 表示运算结果，若x<=y 则 a=1，否则a=0
while(x!=0 && y!=0) {
  x --;
  y --; // 两个循环变量中如果至少有一个减到0，循环退出
}
a = (x==0); // 此时如果x等于零，说明 x 一定是两者中的较小数

发现不难改造成 brainf**k 程序

(push exp)
{
  先复制一个 x 并判断 x 非零
  <
  [->>+>+<<<]>>> 复制 x
  [-<<<+>>>]<<<  左三移动 还原原始数据 x
  >>   判非零
  [
    [-]    循环变量清零
    >+<    右侧位置赋值为1
  ]
  >          找到右侧位置
  [-<+>]<    左一移动

  <
  [->>+>+<<<]>>> 复制 y
  [-<<<+>>>]<<<  左三移动 还原原始数据 y
  >>   判非零
  [
    [-]    循环变量清零
    >+<    右侧位置赋值为1
  ]
  >          找到右侧位置
  [-<+>]<    左一移动
  
  与运算:
  <                  指针对准第一个数
  [[-]>[[-]>+<]<]    如果两个数都非零，那么辅助运算单元会被赋值为1
  [-]>[-]>           清空前两个位置的值
  [-<<+>>]<<         左二移动
}

[[-]       while 循环
  <-      y 自减一
  <-      x 自减一
  >
  
  (push exp)
  {
    先复制一个 x 并判断 x 非零
    <
    [->>+>+<<<]>>> 复制 x
    [-<<<+>>>]<<<  左三移动 还原原始数据 x
    >>   判非零
    [
      [-]    循环变量清零
      >+<    右侧位置赋值为1
    ]
    >          找到右侧位置
    [-<+>]<    左一移动

    <
    [->>+>+<<<]>>> 复制 y
    [-<<<+>>>]<<<  左三移动 还原原始数据 y
    >>   判非零
    [
      [-]    循环变量清零
      >+<    右侧位置赋值为1
    ]
    >          找到右侧位置
    [-<+>]<    左一移动
    
    与运算:
    <                  指针对准第一个数
    [[-]>[[-]>+<]<]    如果两个数都非零，那么辅助运算单元会被赋值为1
    [-]>[-]>           清空前两个位置的值
    [-<<+>>]<<         左二移动
  }
]
此时两个数中已经有一个减到零

<[-]  y 清零
<

(判断 x 为零)
{
  [
    [-]    循环变量清零
    >+<    右侧位置赋值为1
  ]
  +>          置一，并找到右侧位置
  [-<->]<     用一减
}

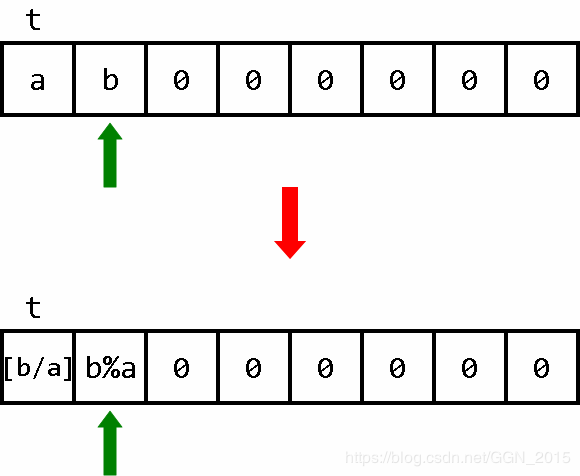
操作5：BYTE除法，求 b除以a的 商 和 余数

原理很简单，在b身上循环减a，直到把 b 减到 a>b 位置。也就是说，只要 $a\le b$，就在 b 身上减去一个 a。判断 $a\le b$ 的方法，可以直接利用操作4。

你可能会感到十分震惊，为什么需要这么多得辅助运算单元？（没错，是因为我懒。）主要是为了直接借用操作4的程序段。每次循环时，我们把 单元t 中的内容复制到 单元t+3 中，把 单元t+1中的内容复制到 单元t+4中 ，然后把指针移动到t+4，进行大小比较。每进行一次减法，就把 单元t+2中的内容自加一，用来记录商（余数会被保存在 单元t+1中）。套用操作4的代码，看似复杂的任务就显得极其简单了。

BYTE除法:
(push x and y)
{
  <                  移动到 x
  [->>>+>+<<<<]>>>>
  [-<<<<+>>>>]<<<<   右三传送
  
  >                  移动到 y
  [->>>+>+<<<<]>>>>
  [-<<<<+>>>>]<<<<   右三传送
  >>>                移动到比较位置
}


(push exp)
{
  先复制一个 x 并判断 x 非零
  <
  [->>+>+<<<]>>> 复制 x
  [-<<<+>>>]<<<  左三移动 还原原始数据 x
  >>   判非零
  [
    [-]    循环变量清零
    >+<    右侧位置赋值为1
  ]
  >          找到右侧位置
  [-<+>]<    左一移动

  <
  [->>+>+<<<]>>> 复制 y
  [-<<<+>>>]<<<  左三移动 还原原始数据 y
  >>   判非零
  [
    [-]    循环变量清零
    >+<    右侧位置赋值为1
  ]
  >          找到右侧位置
  [-<+>]<    左一移动
  
  与运算:
  <                  指针对准第一个数
  [[-]>[[-]>+<]<]    如果两个数都非零，那么辅助运算单元会被赋值为1
  [-]>[-]>           清空前两个位置的值
  [-<<+>>]<<         左二移动
}

[[-]       while 循环
  <-      y 自减一
  <-      x 自减一
  >
  
  (push exp)
  {
    先复制一个 x 并判断 x 非零
    <
    [->>+>+<<<]>>> 复制 x
    [-<<<+>>>]<<<  左三移动 还原原始数据 x
    >>   判非零
    [
      [-]    循环变量清零
      >+<    右侧位置赋值为1
    ]
    >          找到右侧位置
    [-<+>]<    左一移动

    <
    [->>+>+<<<]>>> 复制 y
    [-<<<+>>>]<<<  左三移动 还原原始数据 y
    >>   判非零
    [
      [-]    循环变量清零
      >+<    右侧位置赋值为1
    ]
    >          找到右侧位置
    [-<+>]<    左一移动
    
    与运算:
    <                  指针对准第一个数
    [[-]>[[-]>+<]<]    如果两个数都非零，那么辅助运算单元会被赋值为1
    [-]>[-]>           清空前两个位置的值
    [-<<+>>]<<         左二移动
  }
]
此时两个数中已经有一个减到零

<[-]  y 清零
<

(判断 x 为零)
{
  [
    [-]    循环变量清零
    >+<    右侧位置赋值为1
  ]
  +>          置一，并找到右侧位置
  [-<->]<     用一减
}

比较大小完成

[[-]                 主循环
  <+                 商加一
  <<                 移动到 x
  [->>>+>+<<<<]>>>>
  [-<<<<+>>>>]<<<<   右三传送

  >>>
  [-<<->>]<<         在 y 身上减去 x
  现在指针已经回到y
  
  (push x and y)
  {
    <                  移动到 x
    [->>>+>+<<<<]>>>>
    [-<<<<+>>>>]<<<<   右三传送
    
    >                  移动到 y
    [->>>+>+<<<<]>>>>
    [-<<<<+>>>>]<<<<   右三传送
    >>>                移动到比较位置
  }
  
  
  (push exp)
  {
    先复制一个 x 并判断 x 非零
    <
    [->>+>+<<<]>>> 复制 x
    [-<<<+>>>]<<<  左三移动 还原原始数据 x
    >>   判非零
    [
      [-]    循环变量清零
      >+<    右侧位置赋值为1
    ]
    >          找到右侧位置
    [-<+>]<    左一移动
  
    <
    [->>+>+<<<]>>> 复制 y
    [-<<<+>>>]<<<  左三移动 还原原始数据 y
    >>   判非零
    [
      [-]    循环变量清零
      >+<    右侧位置赋值为1
    ]
    >          找到右侧位置
    [-<+>]<    左一移动
    
    与运算:
    <                  指针对准第一个数
    [[-]>[[-]>+<]<]    如果两个数都非零，那么辅助运算单元会被赋值为1
    [-]>[-]>           清空前两个位置的值
    [-<<+>>]<<         左二移动
  }
  
  [[-]       while 循环
    <-      y 自减一
    <-      x 自减一
    >
    
    (push exp)
    {
      先复制一个 x 并判断 x 非零
      <
      [->>+>+<<<]>>> 复制 x
      [-<<<+>>>]<<<  左三移动 还原原始数据 x
      >>   判非零
      [
        [-]    循环变量清零
        >+<    右侧位置赋值为1
      ]
      >          找到右侧位置
      [-<+>]<    左一移动
  
      <
      [->>+>+<<<]>>> 复制 y
      [-<<<+>>>]<<<  左三移动 还原原始数据 y
      >>   判非零
      [
        [-]    循环变量清零
        >+<    右侧位置赋值为1
      ]
      >          找到右侧位置
      [-<+>]<    左一移动
      
      与运算:
      <                  指针对准第一个数
      [[-]>[[-]>+<]<]    如果两个数都非零，那么辅助运算单元会被赋值为1
      [-]>[-]>           清空前两个位置的值
      [-<<+>>]<<         左二移动
    }
  ]
  此时两个数中已经有一个减到零
  
  <[-]  y 清零
  <
  
  (判断 x 为零)
  {
    [
      [-]    循环变量清零
      >+<    右侧位置赋值为1
    ]
    +>          置一，并找到右侧位置
    [-<->]<     用一减
  }
  
  比较大小完成
]

<<< [-]    清除 x
>>         指针移动到商
[-<<+>>]<< 左二移动 

你别看程序写了200多行，实际上原理是很简单的，把空白和注释都删掉就没有多少了。这个程序的检验用可视化解释器就显得很慢了，不过效果相当震撼。有机会用录屏软件录一个！（一定要注意！除数为0时会死循环！）

+++ 3
>
+++++ +++++ 10

把速度调到最快，在可视化解释其上 这组数据 可以在几分钟内得到结果。用我的简易解释器可以在一秒之内得到结果，这样程序的正确性检验能更快一点，不过就欣赏不到美妙的数据跳动的过程了。

第二章 - 数组寻址操作

如果不过一下脑子，可能还觉得数组寻址操作挺简单的，其实不然，这也就是为什么我觉得应该单独提出一章来探讨数组寻址。

在第一章中，我们介绍了关于BYTE类型的各种运算操作，细心的你一定已经发现了一个惊天的秘密——任意一对匹配的中括号之间的 “左书名号” 与 “右书名号” 的数量总是相等的（什么？你竟然没发现？回去翻代码！）。这是一种非常实用的操作策略，它能保证无论是否进入分支类结构（例如 循环 和 条件判断），程序在结束时指针都会停在同一个位置。我们常利用这个性质来保证指针停留在运算栈的顶部（其实这么说并不确切）。而在第二章中，我们即将打破这个“金科玉律”…

方法1：短数组寻址的实现：“轨道矿车法”

假如你正在一条笔直的大道上行驶，但是你的司机记性很不好（我的记性也不好）。你想让他开车到达一个指定的地方，但是他却说什么也记不住，这可怎么办呢？

昨天晚上失眠的时候，我灵机一动想到了这个办法：

“司机先生，我给你加的油正好足够你从当前位置开车到目的地。一旦到达目的地你的车就是立即因为汽油耗尽而停下，你到那个地方下车去取我让你取得包裹就好了…”

我就是用这种方法来实现短数组寻址的。

我们在线性存储区中构造出一种这样的结构：

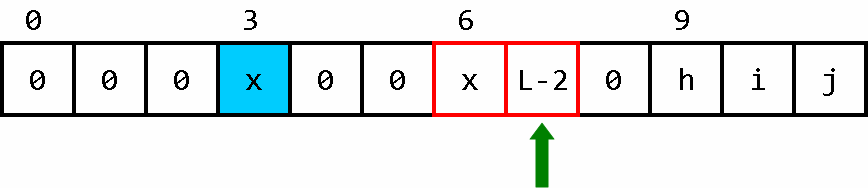
其中，$A_0,A_1,A_2...$为数组中的元素，每相邻的两个数组元素之间有两个空白储存单元（是不是看起来特别像轨道）。我们在此规定，$A_{-1}$所在的位置称为“数组头”，而且在这个数组没有被调用的时候，数组头中储存的元素必须为零。

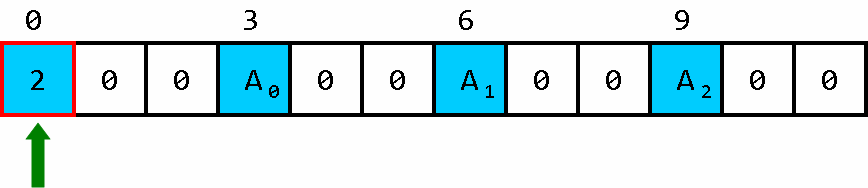
当我们需要调取数组中的某一个元素的时候，我们就把想要调取的位置的下标（例如：$A_0$的下标为0，$A_1$的下标为1…）存放到“数组头中”，然后运行一段固定的程序，就能把想要的值传送到数组头。

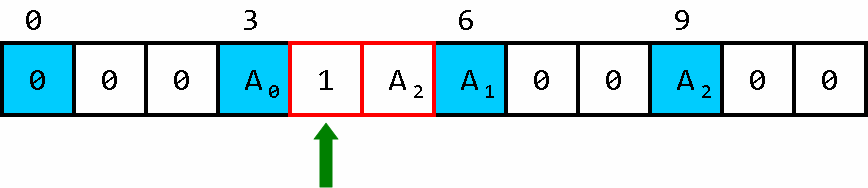
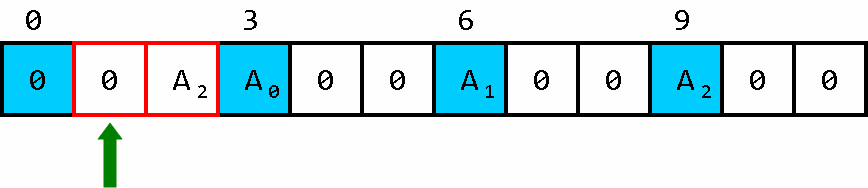
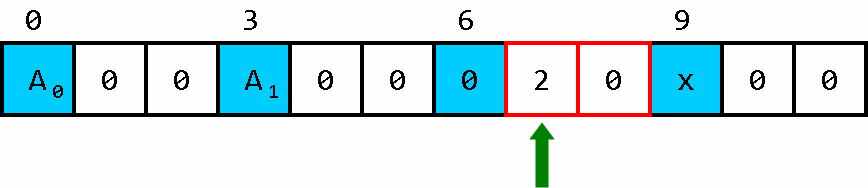
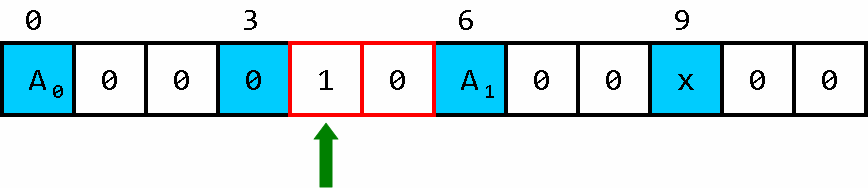
例如我们想要$A_2$中储存的值，看了这组图我猜你就会明白：

想要调用的下标被存入了数组头。

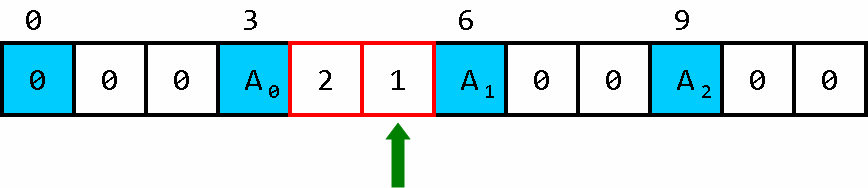
构造出了一台有两个“油箱”的小车，两个油箱分别负责 “去” 和 “回来”。

走了一步，耗了一步的油。

走到了目的地，一个油箱被耗尽，此时用于车子前进的循环体 会退出循环。

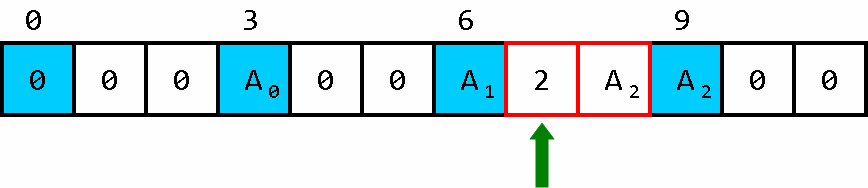
用已经被排空的油箱装载我们要的数据（废物利用，节省空间）。

带着数据前进，耗掉一点油。

返回到起点，油恰好耗尽。

把取到的答案移动到数组头即可。

我们来用 Brainf**k 实现一下这个过程：

构造数据“轨道” 
>>> +++++ >>> +++ >>> ++++
<<<       <<<     <<<       回到数组头 

++     我要下标为2的储存单元中储存的信息

取数操作
[->+>+<<]>> 构造小车 光标移到车头
[-                小车发动 耗油 
  [->>>+<<<]      右三移动 一号油箱 
  <
  [->>>+<<<]      右三移动 二号油箱 
  >>>>            光标移到新的车头 
]

到达目的地 小车开不动了 对目标数据进行左一传送 
>
[-<+>>+<]>  双向复制 （轨道上，右侧恰有空位） 
[-<+>]<     左一移动 

<<                调头 光标移到新的车头
[-                小车发动 耗油 
  [-<<<+>>>]      左三移动 二号邮箱 
  >
  [-<<<+>>>]      左三移动 目标数据
  <<<<            光标移到新的车头 
] 

托运到家
>
[-<<+>>]<<        左二移动 卸货 

（比起BYTE除法运算来说，这个程序是不是简单的多了。）

这种方法可以实现长度不超过256的数组，但是一定要注意，如果你给小车加的油太多了，它可能会开到没有轨道的区域里去横冲直撞，那样程序就会陷入一片混乱…

方法2：短数组的修改

原理很简单，就是给小车加个后备箱，然后带着一个数据跑。但是如果按照这个思路，我们的“轨道间距”就应该从 两个空位 调整成 三个空位。如果不想改变轨道的间距呢？

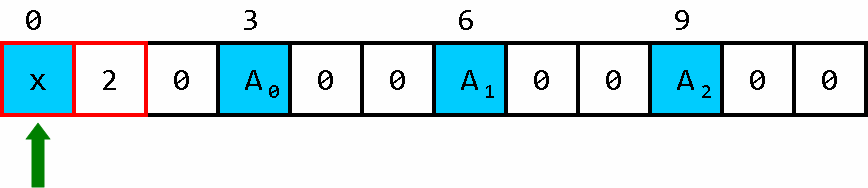
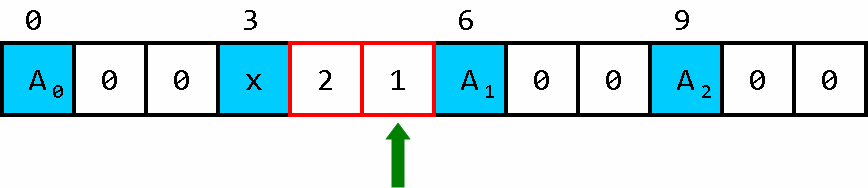
我们以 “把下标为2的位置 储存的信息修改成 x” 为例：

开始时的状态。

构造出小车。

每次小车前进之前，都进行一个操作：把车头前的数 和 车尾后的数 进行交换。然后小车再前进。

这样一来，就好像数据 x 被装进了小车的“后备箱里”。

继续前进，知道一号油箱中的燃料耗尽。

此时调转车头，并将车头前的数清零（因为这个数据应在修改时，应该被 x 覆盖）。

小车逐渐返回，返回与前往的区别在于，在每次前进之后，对车头前的数和车尾后的数进行调换（而不是在前进之前调换）。由于车尾后的数一定是零，所以直接移动即可。

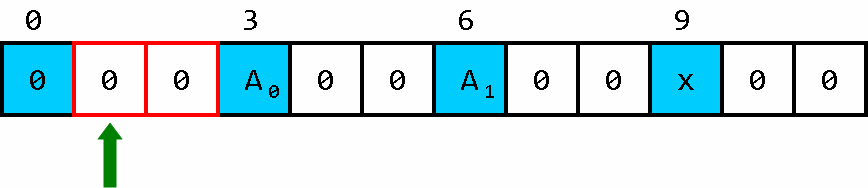
回到出发地，任务完成，调整指针到 单元0 即可。

我们来试着用 brainf**k 去实现一下：

构造数据“轨道” 
>>> +++++ >>> +++ >>> ++++
<<<       <<<     <<<       回到数组头 

+++++ ++ > ++ <        我们这次把 下标为2的位置的值 修改为7

修改操作
>
[->+>>+<<<]>>>
[-<<<+>>>]<<    右一传送 构建小车

[-                   小车前进 耗油 
   前进之前 交换前后 三次移动
   >                 指针到车前 
   [->+<]            右一移动 让位 
   <<<               指针到小车后
   [->>>+<<<]>>>     右三移动
   >
   [-<<<<+>>>>]      左四移动
   <<                指针到车头 
   
   车身前进！ 
   [->>>+<<<]        右三移动
   <
   [->>>+<<<]        右三移动
   >>>>              光标移到车头 
] 

车油耗尽 （请注意，这一段的顺序和图片稍有不符合）
> [-]              扫除前方障碍
<<<
[->>>+<<<]>>>      右三移动
<<                 指针回到新的车头 

[-   小车前进 二号油箱 耗油 
  车身前进！
  [-<<<+>>>]  左三移动 
  >
  [-<<<+>>>]  左三移动
  <<<<        指针移动到新的车头
  
  数据交换
  由于车尾后的值始终是0，直接移动车头前的数即可
  <                指针移动到车头前 
  [->>>+<<<]       右三移动
  >                指针回到车头 
]

<         操作完成 指针归位 

如果你玩过GOL（Game of Life）的话，你就会发现这种“小车”的结构很和GOL中的一些结构十分类似。

方法3：“压路机” 与 轨道构建

其实就是c++中的memset操作…

我们可以用类似于上文中的小车的方法构造一个具有“轨道”结构的数组。

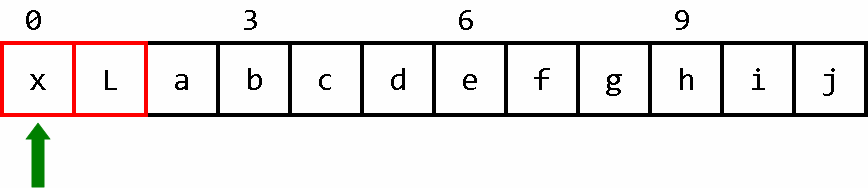
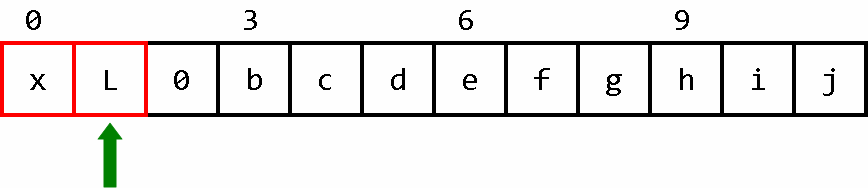
我们要建立一个下标区间为[0,L]的数组。

压路机准备启动，清空车前的“障碍”。

压路机继续前进。

从第二次前进开始，压路机会把信息 x 以传送的方式向前转移。

这种压路机有去无回，适合用来在程序柱体开始前使用，用来构建程序的 堆空间（程序的栈空间直接接在堆空间的后面即可）。

代码懒得写了…同理还有带有返回功能的压路机，在构建轨道完成后可以把指针返回到出发点。

（“还不快去写寒假作业！马上就要开学了！”，“好吧(╯▽╰)，只好先把博文写到这了…”）

第三章 - 中间语言的设计实践

第一步：对底层中间语言的设计

为了简化整个程序设计过程，我打算采用这样的方法：把前文中我们已经设计好的一些程序段用一些“助记符”表示，然后再写一个C++程序把这个写满助记符的程序翻译成brainf**k。

学着汇编语言的模样照葫芦画瓢即可，只是没有了条件跳转指令。

规定助记符（中括号内部表示操作数）：

push_imm [常数] 立即数进栈

push_var [常数] 变量进栈（常数为变量存储单元位置）

pop_out 弹出栈顶

pop_var [常数] 弹出栈顶存入变量

trans 查表转换（取堆空间中的元素）

retrans 把数值存回堆空间

ADD,SUB,MUL,DIV 栈顶处的BYTE数值运算

AND,OR,NOT 逻辑运算

EXCH 交换栈顶两个元素

equ_zero,neq_zero 判断栈顶元素等于零/不等于零

leq_signed,leq_unsigned 判断小于等于（有符号BYTE，无符号BYTE）

INP,OUTP 输入字符/输出字符

流程控制指令：

if_real ... endif_real 单支路条件判断

if ... else ... endif 双支路条件判断

do ... loop 中括号直接实现的循环

for ... endfor 循环变量每次自减一的 for 循环

为了方便起见，写了一个没有什么用的程序：

#include 
#include 
#include 
using namespace std;

void comdel(FILE* fpin, FILE* fpout) { /// 删除 brfk 程序中的注释 
    char c = fgetc(fpin);
    while(c != EOF) {
        if(c=='[' || c==']' || c=='<' || c=='>' || c==',' || c=='.' || c=='+' || c=='-')
            fputc(c, fpout);
        c = fgetc(fpin);
    }
    fclose(fpin);
    fclose(fpout);
}

int main() {
    FILE* fpin  = fopen("main.brfk", "r");
    FILE* fpout = fopen("outp.brfk", "w");
    comdel(fpin, fpout);
    system("pause");
    return 0;
}

用一个巨ZZ的替换程序进行文本替换：

#include 
#include 
using namespace std;

bool strsame(const char* s, const char* t) {
    for(int i = 0; ; i ++) {
        if(s[i] != t[i])
            return false;
        if(s[i] == 0)
            break;
    }
    return true;
}

#define r_in(A, B, C) (((A)<=(B)) && ((B)<=(C)))

bool checkint(const char* s) {
    for(int i = 0; s[i]; i ++) {
        if(!r_in('0', s[i], '9')) return false;
    }
    return true;
}

void loopOutput(const char* s, FILE* fpout, int t) {
    for(int i = 1; i <= t; i ++) {
        fprintf(fpout, "%s", s);
        if(i%5  == 0) fprintf(fpout, " ");
        if(i%10 == 0) fprintf(fpout, "    ");
    }
}

/// 这真是我本世纪以来写过的最傻的程序 

void work(FILE* fpin, FILE* fpout) {
    char tmp[260] = {};
    fscanf(fpin, "%s", tmp);
    int stack_top = 0;
    while(!strsame(tmp, "END") && !strsame(tmp, "")) { /// 我才懒得写自动机 
        if(strsame(tmp, "{")) { /// comment
            while(!strsame(tmp, "}")) {
                fscanf(fpin, "%s", tmp);
            }
        }else if(strsame(tmp, "push_imm")) {
            fscanf(fpin, "%s", tmp);
            if(!checkint(tmp)) {
                printf("error: sth after push_imm which is not integer value.\n");
                system("pause");
            }
            int imm = 0;
            sscanf(tmp, "%d", &imm);
            fprintf(fpout, "push_imm %3d > ", imm);
            loopOutput("+", fpout, imm);
            fprintf(fpout, "\n");
            stack_top ++; /// 调整栈顶指针位置 
        }else if(strsame(tmp, "push_var")) {
            fscanf(fpin, "%s", tmp);
            if(!checkint(tmp)) {
                printf("error: sth after push_var which is not integer value.\n");
                system("pause");
            }
            int var = 0;
            sscanf(tmp, "%d", &var);
            fprintf(fpout, "push_var %3d ", var);
            int cnt = stack_top-var; /// 计算路程差 
            loopOutput("<", fpout, cnt); /// 移动到变量处 
            fprintf(fpout, " [-"); /// 复制
            loopOutput(">", fpout, cnt+1); /// 移动到新栈顶 
            fprintf(fpout, "+>+<");
            loopOutput("<", fpout, cnt+1); /// 移动回变量 
            fprintf(fpout, "] ");
            loopOutput(">", fpout, cnt+2); /// 移动到新栈顶的下一个位置 
            fprintf(fpout, " [-");
            loopOutput("<", fpout, cnt+2); /// 回到变量 
            fprintf(fpout, "+");
            loopOutput(">", fpout, cnt+2); /// 回到新栈顶的下一个位置 
            fprintf(fpout, "] <"); /// 回到新栈顶 
            fprintf(fpout, "\n");
            stack_top ++; /// 调整栈顶指针位置 
        }else if(strsame(tmp, "pop_out")) {
            fprintf(fpout, "pop_out      [-] <\n");
            stack_top --;
        }else if(strsame(tmp, "pop_var")) {
            fscanf(fpin, "%s", tmp);
            if(!checkint(tmp)) {
                printf("error: sth after pop_var which is not integer value.\n");
                system("pause");
            }
            int var = 0;
            sscanf(tmp, "%d", &var);
            fprintf(fpout, "pop_var  %3d ", var);
            int cnt = stack_top-var;
            fprintf(fpout, "[-");
            loopOutput("<", fpout, cnt);
            fprintf(fpout, "+");
            loopOutput(">", fpout, cnt);
            fprintf(fpout, "]");
            fprintf(fpout, " <\n");
            stack_top --; /// must remember
        }else if(strsame(tmp, "ADD")) {
            
        }else {
            printf("error: ins {%s} no exist.\n", tmp)
            system("pause");
        }
        fscanf(fpin, "%s", tmp); /// read new ins
    }
    fclose(fpin);
    fclose(fpout);
}

int main() {
    FILE* fpin  = fopen("main.step", "r");
    FILE* fpout = fopen("main.brfk", "w");
    work(fpin, fpout);
    return 0;
}

2019.1.21 未完待续