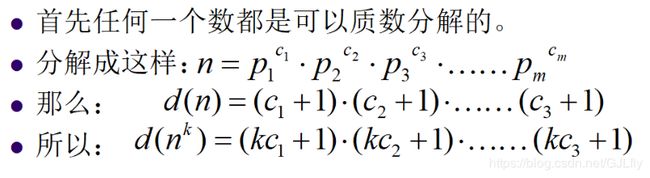Counting Divisors HDU - 6069

In mathematics, the function d(n)d(n) denotes the number of divisors of positive integer nn. 

For example, d(12)=6d(12)=6 because 1,2,3,4,6,121,2,3,4,6,12 are all 1212's divisors. 

In this problem, given l,rl,r and kk, your task is to calculate the following thing : 

(∑i=lrd(ik))mod998244353(∑i=lrd(ik))mod998244353

 

Input

The first line of the input contains an integer T(1≤T≤15)T(1≤T≤15), denoting the number of test cases.

In each test case, there are 33 integers l,r,k(1≤l≤r≤1012,r−l≤106,1≤k≤107)l,r,k(1≤l≤r≤1012,r−l≤106,1≤k≤107).

Output

For each test case, print a single line containing an integer, denoting the answer.

Sample Input

3
1 5 1
1 10 2
1 100 3

Sample Output

10
48
2302

题解：上图来自https://blog.csdn.net/protecteyesight/article/details/76685920

所以只需打表10e6内的素数，再由素数去求l~r，最后相加取余。

#include
#include