常见的五种神经网络(3)-循环神经网络(中)篇
转载请注明出处:https://thinkgamer.blog.csdn.net/article/details/100709422
博主微博:http://weibo.com/234654758
Github:https://github.com/thinkgamer
公众号:搜索与推荐Wiki
引言
常见的五种神经网络系列第三种,主要介绍循环神经网络,分为上中下三篇进行介绍,本文主为(中)篇,涉及内容如下:
- 循环神经网络中的参数学习
- RNN中的长期依赖问题
- 常见的循环神经网络结构
该系列的其他文章:
- 常见的五种神经网络(1)-前馈神经网络
- 常见的五种神经网络(2)-卷积神经网络
- 常见的五种神经网络(3)-循环神经网络(上篇)
- 常见的五种神经网络(3)-循环神经网络(中篇)
- 常见的五种神经网络(3)-循环神经网络(下篇)
- 常见的五种神经网络(4)-深度信念网络
- 常见的五种神经网络(5)-生成对抗网络
参数学习
循环神经网络的参数可以通过梯度下降方法来学习。给定一个样本(x,y),其中 x 1 : T = ( x 1 , x 2 , . . . , x T ) x_{1:T}=(x_1, x_2, ... ,x_T) x1:T=(x1,x2,...,xT)为长度是T的输入序列,其中 y 1 : T = ( y 1 , y 2 , . . . , y T ) y_{1:T}=(y_1, y_2, ... ,y_T) y1:T=(y1,y2,...,yT)是长度为T的标签序列,在每个时刻t,都有一个监督信息 y t y_t yt,定义时刻t的损失函数为(公式1-1):
L t = L ( y t , g ( h t ) ) L_t = L(y_t, g(h_t)) Lt=L(yt,g(ht))
其中 g ( h t ) g(h_t) g(ht)为第t时刻的输出,L为可微分的损失函数,比如交叉熵,整个序列上的损失函数为(公式1-2):
L = ∑ t = 1 T L t L = \sum_{t=1}^{T} L_t L=t=1∑TLt
整个序列的损失函数L关于参数U的梯度为(公式1-3):
∂ L ∂ U = ∑ t = 1 T ∂ L t ∂ U \frac{\partial L}{\partial U} = \sum _{t=1}^{T}\frac{\partial L_t}{ \partial U } ∂U∂L=t=1∑T∂U∂Lt
即每个时刻的损失函数 L t L_t Lt对参数U的偏导数之和。
在循环神经网络中主要有两种计算梯度的方式:
- 随时间反向传播算法(Backpropagation Through Time,BRTT)
- 实时循环学习(Real-Time Recurrent Learning,RTRL)
随时间反向传播算法
主要通过类似前馈神经网络的错误反向传播算法来进行计算梯度。随时间反向传播算法将循环神经网络看作是一个展开的多层前馈网络,其中“每一层”对应循环网络中的每个时刻,这样循环神经网络就可以按照前馈神经网络中的反向传播算法来计算梯度。与前馈神经网络不同的是,循环神经网络中各层的参数是共享的,因此参数的真实梯度是各个层的参数梯度之和。
先计算公式1-3中第t时刻损失对参数U的偏导数 ∂ L t ∂ U \frac {\partial L_t}{\partial U} ∂U∂Lt,参数U和每个时刻k的净输入 z k = U h k − 1 + W x k + b z_k = Uh_{k-1} + Wx_{k} + b zk=Uhk−1+Wxk+b有关,因此第t个时刻损失函数 L t L_t Lt关于参数 U i j U_ij Uij的梯度为(公式1-4):
∂ L t ∂ U i j = ∑ k = 1 t t r ( ( ∂ L t ∂ z k ) T ∂ + z k ∂ U i j ) = ∑ k = 1 t ( ∂ + z k ∂ U i j ) T ∂ L t ∂ z k \frac{\partial L_t}{ \partial U_{ij}} = \sum_{k=1}^{t} tr( ( \frac{\partial L_t}{ \partial z_k} )^T \frac{\partial^+ z_k}{ \partial U_{ij}} ) \\ = \sum_{k=1}^{t} ( \frac{\partial^+ z_k}{ \partial U_{ij}} )^T \frac{\partial L_t}{ \partial z_k} ∂Uij∂Lt=k=1∑ttr((∂zk∂Lt)T∂Uij∂+zk)=k=1∑t(∂Uij∂+zk)T∂zk∂Lt
其中 ∂ + z k ∂ U i j \frac{\partial^+ z_k}{ \partial U_{ij}} ∂Uij∂+zk 表示“直接”偏导数,即公式 z k = U h k − 1 + W x k + b z_k = Uh_{k-1} + Wx_{k} + b zk=Uhk−1+Wxk+b中保持 h k − 1 h_{k-1} hk−1不变,对 U i j U_{ij} Uij进行求偏导数,得到(公式1-5):
∂ + z k ∂ U i j = [ 0 . . . [ h k − 1 ] j . . . 0 ] ≜ I i ( [ h k − 1 ] j ) \frac{\partial^+ z_k}{ \partial U_{ij}} = \begin{bmatrix} 0\\ ... \\ [h_{k-1}]_j \\ ... \\ 0 \end{bmatrix} \triangleq I_i([h_{k-1}]_j) ∂Uij∂+zk=⎣⎢⎢⎢⎢⎡0...[hk−1]j...0⎦⎥⎥⎥⎥⎤≜Ii([hk−1]j)
其中 [ h k − 1 ] j [h_{k-1}]_j [hk−1]j为第 k − 1 k-1 k−1时刻隐状态的第j维, I i ( x ) I_i(x) Ii(x)除了第j行值为x,之外全为0的向量。
定义 δ t , k = ∂ L t ∂ z k \delta _{t,k} = \frac{\partial L_t}{ \partial z_k } δt,k=∂zk∂Lt为第t时刻损失函数对第k时刻隐藏层神经元净输入 z k z_k zk的导数,则(公式1-6):
δ t , k = ∂ L t ∂ z k = ∂ h k ∂ z k ∂ z k + 1 ∂ h k ∂ L t ∂ z k + 1 = d i a g ( f ′ ( z k ) ) U T δ t , k + 1 \delta _{t,k} = \frac{\partial L_t}{ \partial z_k } \\ = \frac{ \partial h_k }{ \partial z_k} \frac{\partial z_{k+1}}{ \partial h_k } \frac{ \partial L_t }{ \partial z_{k+1} } \\ = diag(f'(z_k))U^T \delta _{t,k+1} δt,k=∂zk∂Lt=∂zk∂hk∂hk∂zk+1∂zk+1∂Lt=diag(f′(zk))UTδt,k+1
将(公式1-6) 和 (公式 1-5) 代入(公式1-4)得到(公式1-7):
∂ L t ∂ U i j = ∑ k = 1 t [ δ t , k ] i [ h k − 1 ] j \frac{\partial L_t}{ \partial U_{ij} } = \sum_{k=1}^{ t } [\delta _{t,k}]_i [h_{k-1}]_j ∂Uij∂Lt=k=1∑t[δt,k]i[hk−1]j
将(公式1-7)写成矩阵形式为(公式1-8):
∂ L ∂ U = ∑ k = 1 t δ t , k h k − 1 T \frac{\partial L}{ \partial U } = \sum_{k=1}^{ t } \delta _{t,k} h^T_{k-1} ∂U∂L=k=1∑tδt,khk−1T
下图为随时间反向传播算法示例:
将(公式1-8)代入(公式1-3)得到整个序列的损失函数 L L L关于参数 U U U的梯度(公式1-9):
∂ L ∂ U = ∑ t = 1 T ∑ k = 1 t δ t , k h k − 1 T \frac{\partial L}{ \partial U } = \sum_{t=1}^{ T}\sum_{k=1}^{ t } \delta _{t,k} h^T_{k-1} ∂U∂L=t=1∑Tk=1∑tδt,khk−1T
同理可得到 L L L关于参数 W W W的梯度(公式1-10):
∂ L ∂ W = ∑ t = 1 T ∑ k = 1 t δ t , k x k T \frac{\partial L}{ \partial W } = \sum_{t=1}^{ T}\sum_{k=1}^{ t } \delta _{t,k} x^T_k ∂W∂L=t=1∑Tk=1∑tδt,kxkT
L L L关于参数 b b b的梯度(公式1-11):
∂ L ∂ b = ∑ t = 1 T ∑ k = 1 t δ t , k \frac{\partial L}{ \partial b } = \sum_{t=1}^{ T}\sum_{k=1}^{ t } \delta _{t,k} ∂b∂L=t=1∑Tk=1∑tδt,k
在 随时间反向传播算法中,参数的梯度需要在一个完整的“向前”计算和“向后”计算后才能得到并参数更新。
实时循环学习
与随时间反向传播算法不同的是:实时循环学习(Real-Time Recurrent Learning)是通过前向传播的方式来计算梯度。
假设RNN中第 t + 1 t+1 t+1时刻的状态 h t + 1 h_{t+1} ht+1为(公式1-12):
h t + 1 = f ( z t + 1 ) = f ( U h k + W x k + 1 + b ) h_{t+1} = f(z_{t+1}) = f(Uh_k + Wx_{k+1} + b) ht+1=f(zt+1)=f(Uhk+Wxk+1+b)
其关于参数KaTeX parse error: Expected '}', got 'EOF' at end of input: U_{ij的偏导数为(公式1-13):
h t + 1 ∂ U i j = ∂ h t + 1 ∂ z t + 1 ( ∂ + z t + 1 ∂ U i j + U ∂ h t ∂ U i j ) = d i a g ( f ′ ( z t + 1 ) ) ( I i ( [ h t ] j ) + U ∂ h t ∂ U i j ) = f ′ ( z t + 1 ) ⊙ ( I i ( [ h t ] j ) + U ∂ h t ∂ U i j ) \frac{ h_{t+1} }{ \partial U_{ij} } = \frac{ \partial h_{t+1} }{ \partial z_{t+1} } ( \frac{ \partial^+z_{t+1} }{ \partial U_{ij}} + U \frac{ \partial h_t}{ \partial U_{ij} } ) \\ = diag( f'(z_{t+1}) ) ( I_i ([h_t]_j)+ U \frac{ \partial h_t}{ \partial U_{ij} } ) \\ =f'(z_{t+1}) \odot ( I_i ([h_t]_j)+ U \frac{ \partial h_t}{ \partial U_{ij} } ) ∂Uijht+1=∂zt+1∂ht+1(∂Uij∂+zt+1+U∂Uij∂ht)=diag(f′(zt+1))(Ii([ht]j)+U∂Uij∂ht)=f′(zt+1)⊙(Ii([ht]j)+U∂Uij∂ht)
其中 I i ( x ) I_i(x) Ii(x)为除了第i行之外元素全为0的向量。
RTRL自从第一个时刻开始,除了计算RNN的隐状态之外,还利用(公式1-13)依次前向计算偏导数 ∂ h 1 ∂ U i j , ∂ h 2 ∂ U i j , ∂ h 3 ∂ U i j . . . \frac{\partial h_1}{ \partial U_{ij}},\frac{\partial h_2}{ \partial U_{ij}},\frac{\partial h_3}{ \partial U_{ij}}... ∂Uij∂h1,∂Uij∂h2,∂Uij∂h3...
这样假设第t个时刻存在一个监督信息,其损失函数为 L t L_t Lt,就可以同时计算损失函数对 U i j U_{ij} Uij的偏导数(公式1-14):
∂ L t ∂ U i j = ( ∂ h t ∂ U i j ) T ∂ L t ∂ h t \frac{\partial L_t}{ \partial U_{ij}} =( \frac{\partial h_t}{ \partial U_{ij} } )^T \frac{\partial L_t}{ \partial h_t} ∂Uij∂Lt=(∂Uij∂ht)T∂ht∂Lt
这样在第t个时刻就可以实时计算 L t L_t Lt关于参数U的梯度,并更新参数。参数W和b的梯度也可以按照上述方法进行计算。
两种算法比较:RTRL算法和BPTT算法都是基于梯度求解参数,分别通过前向模式和反向模式应用链式法则来计算梯度。在RNN中一般输出维度要比输入维度少,因此BPTT算法的计算量会很小,但要保存计算过程中的梯度值,空间复杂度较高。RTRL算法不需要进行空间回传,比较适合用在在线学习或无限序列的任务中。
长期依赖
在BRTT算法中,将(公式1-6)展开得到(公式1-15):
δ t , k = ∏ i = k t − 1 ( d i a g ( ′ f ( z i ) ) U T ) δ t , t \delta _{t,k}=\prod_{i=k}^{t-1} ( diag('f(z_i ))U^T )\delta _{t,t} δt,k=i=k∏t−1(diag(′f(zi))UT)δt,t
如果定义 γ ≈ ∣ ∣ d i a g ( ′ f ( z i ) ) U T ∣ ∣ \gamma \approx || diag('f(z_i ))U^T || γ≈∣∣diag(′f(zi))UT∣∣,则(公式1-16):
δ t , k = γ t − k δ t , t \delta _{t,k}=\gamma ^{t-k} \delta _{t,t} δt,k=γt−kδt,t
若 γ > 1 \gamma >1 γ>1,当 t − k → + ∞ t-k \rightarrow +\infty t−k→+∞, γ t − k → + ∞ \gamma ^{t-k} \rightarrow +\infty γt−k→+∞,会造成系统不稳定,称之为梯度爆炸(Gradient Exploding Problem),反之,若 γ < 1 \gamma < 1 γ<1,当 t − k → + ∞ t-k \rightarrow +\infty t−k→+∞, γ t − k → 0 \gamma ^{t-k} \rightarrow 0 γt−k→0,会出现和前馈神经网络类似的梯度消失问题(Gradient Vanishing Problem)。
注意:在循环神经网络中,梯度消失指的是并不是说 ∂ L t ∂ U \frac{ \partial L_t}{ \partial U} ∂U∂Lt的梯度消失了,而是 ∂ L t ∂ h k \frac{ \partial L_t}{ \partial h_k} ∂hk∂Lt的梯度消失,当 t − k t-k t−k很大时,即参数U的更新主要靠最近的几个状态来更新,长距离的状态对参数U没有影响。
当循环神经网络中使用的激活函数是Logistic或者tanh的时候,由于其导数小于1,并且权重矩阵 ∣ ∣ U ∣ ∣ ||U|| ∣∣U∣∣也不会太大,因此,如果时间间隔t-k过大的话,也会出现梯度消失问题。所以一般采用 ReLU激活函数(关于激活函数的介绍可参考:神经网络中的激活函数介绍)。
虽然简单循环网络理论上可以建立长时间间隔的状态之间的依赖关系,但是由于梯度爆炸和梯度消失问题,实际上只能学习到短期的依赖关系,这样如果t时刻的输出 y t y_t yt依赖于 t − k t-k t−k时刻的输入 x t − k x_{t-k} xt−k,当间隔k比较大时,简单神经网络很难建模这种长距离的依赖关系,称之为长期依赖问题(Long-Term Dependences Problem)。
改进措施:
- 选取合适的参数
- 使用非饱和的激活函数
循环网络的梯度爆炸问题比较容易解决,一般通过梯度截断和权重衰减来避免。而梯度消失很难解决,通常是对模型进行调优来解决。
常见的循环神经网络结构
主要包含四种:
- N:N
- 1:N
- N:1
- N:M
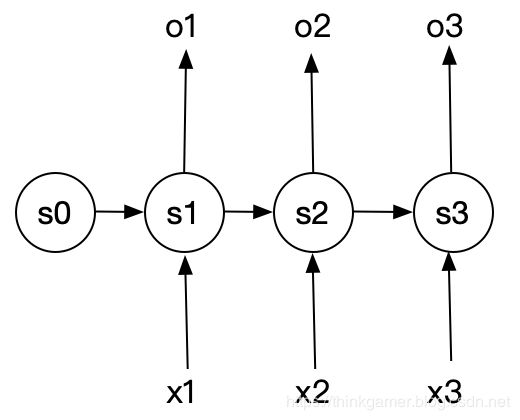
N比N结构
N维输入对应N维输出,大致结构如下所示:
其常常用于处理以下问题:
- 视频理解中获取视频每一帧标签,输入为视频解码后的图像,通过此结构,获取每一 帧的标签信息。这种场景一般用作视频理解的初期,对视频做初步的处理后, 后续可以基于这些标签信息进行语义分析,构建更为复杂的需求场景。
- 股票价格预测。基于历史的股票信息输入,预测下一时刻或者未来的股票走势信息。
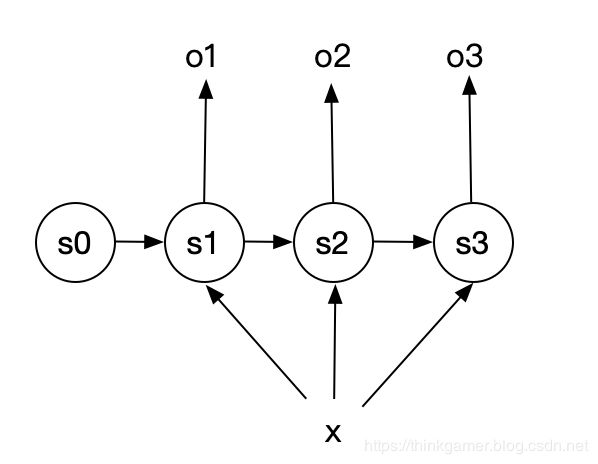
1比N结构
其常常用于处理以下问题:
- 看图写描述 : 根据输入的 一张图 片,生成对这张图片的描述信息
- 自动作曲 : 按照类别生成音乐
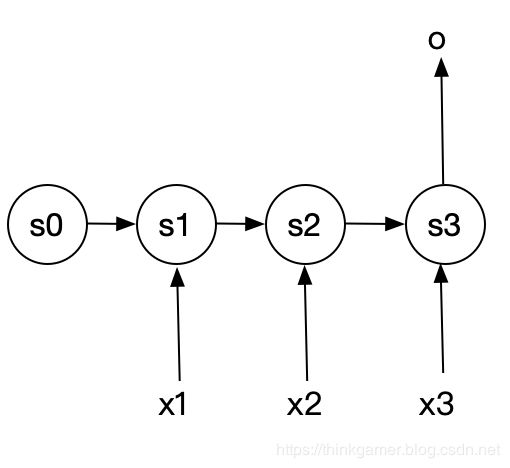
N比1结构
其常常用于处理以下问题:
- 视频理解中的获取视频每个场景的描述信息,或者获取整个影片的摘要信息。
- 获取用户评价的情感信息,即根据用户的一句话的评论,来判断用户的喜好等情感信息 。
N比M结构
N维输入,M维输出,这种结构又被称为Encoder-Decoder模型,也可以称为Seq2Seq模型,这种模型的输入和输出可以不相等,该模型由两部分组成:编码部分和解码部分,大致结构如下图所示:
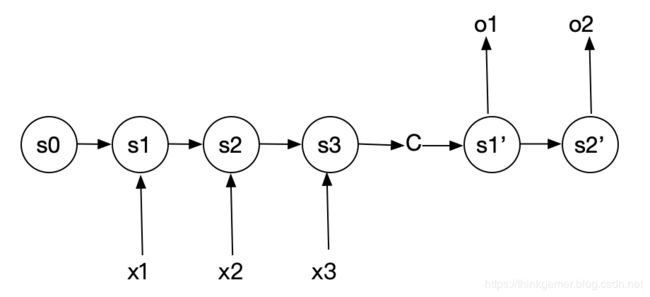
c的前半部分循环神经网络为编码部分,称之为Endcoder, c可以是s3的直接输出,或者 是对s3输出做一定的变换,也可以对编码部分所有的s1、s2、s3进行变换得到,这样c中就包 含了对X1、 Xz、码的编码信息 。c的后半部分循环神经网络为解码部分,称之为Decoder。c作为之前的状态编码,作为初始值,输入到Decoder当中。 Decoder经过循环处理,最终将信息解码输出。
N比M的循环神经网络结构更具有普遍性,现实环境中有很多基于该结构落地的场景,他可以解决如下问题:
- 机器翻译:将不同语言作为输入,输出为非输入语言的类型,这也是Encoder-Decoder的经典用法
- 文本摘要:输入一篇文章,输出这篇文章的摘要信息
- 语音识别:输入一段语音,输出这段语音信息的文字
至此,循环神经网络(中)篇已经介绍完了,在下篇中会展开介绍更多的内容,欢迎关注。

【搜索与推荐Wiki】专注于搜索和推荐系统,尝试使用算法去更好的服务于用户,包括但不局限于机器学习,深度学习,强化学习,自然语言理解,知识图谱,还不定时分享技术,资料,思考等文章!