LBP特征提取的实现以及思考
LBP特征提取的实现以及思考
LBP(local binary pattern),局部二值模式,主要应用与图像的特征提取,比如人脸识别,车牌识别等领域。之所以广泛的使用原因就在于LBP算子,可以有效地应对光照的影响,最原始的LBP称为灰度不变模式(gray_scale invariant pattern)意思也就是其对光照的很强的鲁棒性。那为什么灰度光照有如此好的鲁棒性呢?
灰度不变模式
原始的LBP算子,原理是构造一个3*3的模板,在这样的一个模板中以中心像素的灰度值为阈值,进行二值化。当模板内的邻域像素大于中心像素,则将邻域处记为1,否则记为0,然后按照顺时针或者逆时针的顺序对所得到0,1序列进行编码。由于我们这里使用的是3*3的邻域模板,因此会得到8位二进制码,将此8位二进制码展开为十进制数,就是所得到的LBP值,遍历原图的每一个像素,得到的新的图像,就是原始图像的LBP图像。之所以我们称这样的一种方式为灰度不变模式,原因在于在这样的模板里,我们关注的是中心像素与邻域像素的相对关系,而不再是全局的灰度值与某一点像素的关系,这样进行局部的二值化时只会在明暗变化明显的(交界处)才会出现明显的边缘。即使在全图上存在多个光照不均匀的地方,但是局部二值化时,这些不均匀的地方就变成了均匀的。因此LBP对光照具有很强的鲁棒性。
实现方法:
在这里我们需要注意几点:
1, 输出的LBP图像的大小。Dst.create(src.rows – 2,src.cols -2 ,CV_8UC1).原因就在于要保证邻域范围的安全计算。由于原始的LBP是3*3的邻域,所以是“-2”。
2, 在整个的LBP算法实现过程中,最主要的是对于C++中位运算的掌握。按位与,按位或(主要),以及左移,右移的计算。
实现代码:
void getorigianlLBP(const Mat &src, Mat &dst) //8邻域
{
if(src.empty())
{
cout << “The image is empty! please check your data!” << endl;
exit(0);
}
Mat gray_image;
if(src.channels() == 3)
{
cvtColor(src,gray_image,CV_BGR2GRAY);
}
else
{
gray_image = src;
}
int rows_num = src.rows;
int cols_num = src.cols;
dst = Mat::zeros(rows_num - 2,cols_num - 2,CV_8UC1);
for (int i = 1; i < rows_num - 1;i++)
{
for(int j = 1; j < cols_num - 1; j++)
{
uchar center_pix = gray_image.at(i,j); //gray_image 不是 src
unsigned char lbpcode = 0;
lbpcode |= ( gray_image.at(i-1,j-1) > center_pix) << 7;
lbpcode |= ( gray_image.at(i-1,j) > center_pix) << 6;
lbpcode |= ( gray_image.at(i-1,j+1) > center_pix) << 5;
lbpcode |= ( gray_image.at(i,j+1) > center_pix) << 4;
lbpcode |= ( gray_image.at(i+1,j+1) > center_pix) << 3;
lbpcode |= ( gray_image.at(i+1,j) > center_pix) << 2;
lbpcode |= ( gray_image.at(i+1,j-1) > center_pix) << 1;
lbpcode |= ( gray_image.at(i,j-1) > center_pix) << 0;
/*
lbpcode |= ( center_pix > gray_image.at(i-1,j-1)) << 7;
lbpcode |= ( center_pix > gray_image.at(i-1,j)) << 6;
lbpcode |= ( center_pix > gray_image.at(i-1,j+1)) << 5;
lbpcode |= ( center_pix > gray_image.at(i,j+1)) << 4;
lbpcode |= ( center_pix > gray_image.at(i+1,j+1)) << 3;
lbpcode |= ( center_pix > gray_image.at(i+1,j)) << 2;
lbpcode |= ( center_pix > gray_image.at(i+1,j-1)) << 1;
lbpcode |= ( center_pix > gray_image.at(i,j-1)) << 0;
*/
dst.at(i-1,j-1) = lbpcode;
}
}
if(1)
{
static int cnt = 0;
char file_name[128];
snprintf(file_name,sizeof(file_name),"/tmp/res/lbp/original_%d.bmp",++cnt);
easypr::utils::imwrite(file_name,src);
}
if(1)
{
static int cnt = 0;
char file_name[128];
snprintf(file_name,sizeof(file_name),"/tmp/res/lbp/gray_image_%d.bmp",++cnt);
easypr::utils::imwrite(file_name,gray_image);
}
if(1)
{
static int cnt = 0;
char file_name[128];
snprintf(file_name,sizeof(file_name),"/tmp/res/lbp/originallbp_%d.bmp",++cnt);
easypr::utils::imwrite(file_name,dst);
}
}
圆形邻域模式
由于原始的LBP使用的是3*3的邻域,这样对于图像中的每一个像素点采样点的围相对较小。为了可以关于中心像素点的更多的纹理信息。因此我们定义了LBP(P,R)模式,这里的P 表示的是采样点的个数,这里的R表示的是采样得半径。也就是我们将原始的方形邻域改为了圆形邻域。这个圆形邻域的大小通过半径R来控制。同时为了在新的圆形邻域上得到图像的详细的纹理信息。我们用P来规定圆形邻域的采样点。由于圆形邻域上进行采样,相邻两个采样点之间的角度为2*pi / P;这样可能对于某一些采样点会不在某一个完整的像素点上。为了得到这个点的灰度值以便进行二值化编码。我们需要对这些新的采样点进行插值计算,目前使用最广泛的就是双线性插值计算。下面我们分别说明新的采样点的位置,以及双线性差值的计算方法。
注意我们这里从图像坐标系来说明计算方法:
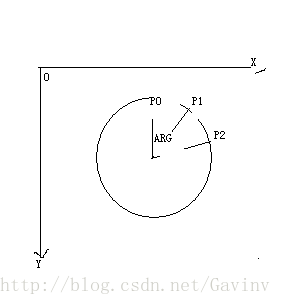
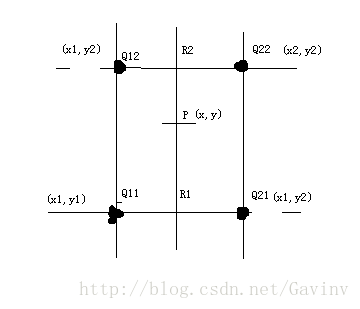
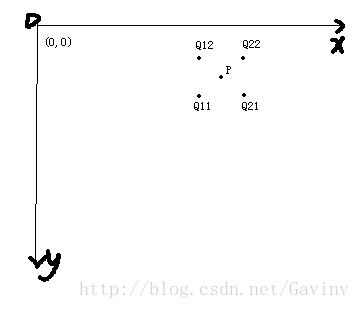
上面的三张图分别是采样点分布图,双线性插值示意图,在图像中的的双线性插值示意图。
从图1中我们可以看出,相邻的采样点之间的夹角ARG = 2*PI / P;(P为采样点),由此可知Pi处的位置坐标是XI = x + r*cos(ARG); YI = y – r*sin(ARG); 以上的公式是在平面坐标系下的位置计算公式。当映射到实际的图像坐标中时需要考虑实际图像坐标的坐标系特点。也就是说,在实际的图像坐标系中 XI = x + cos(ARG); YI = y – sin(ARG);从公式上来看是一致的。通过这样的计算之后,我们可以获得采样点的位置,但是这个计算结果未必是整数。所以我们需要对计算出来的位置进行双线性插值。在代码里我们使用floor向上取整,ceil向下取整来分别获得XI,YI对应的四个X,Y的值。对于floor和ceil的运算,floor(0.56) = 0; ceil(0.56) = 1; floor(-1.23) = -2; ceil(-1.23) = -1;切记向上取整,和向下取整的不同,记忆的时候只要记住floor取值更小,ceil取值更大。
双线性插值:所谓的双线性插值,实际上就是对X,Y方向的线性插值。线性差值的公式是如下图所示实际上就是保持插值点处的斜率与原来的斜线的斜率是一致的。
那么当我们对P0点进行插值的时候,我们所需要找到的对应关系为arg1 = arg2;由这样的关系我们可以得到,(y0 – y1) / (x0 –x1) = (y2 – y1) / (x2 – x1) ;实际上就是斜率不变,我们通常写成林外一种形式。(y0 – y1) / (y2 – y1) = (x0 –x1) / (x2 –x1);
这就是线性差值的原理。同样的,当我们进行双线性插值的时候实际上就是在X,Y两个方向上进行的线性插值。如上图的图2可知,当我们对图中的P点进行插值时,我们已知Q11,Q12,Q21,Q22这四个点的值。以及这四个点的位置坐标。
1, 先在X方向进行线性插值
为了更加明确一下线性插值与双线性插值的关系,我们假设(Y0 – Y1)/ (y2 – y1) =
(x0 –x1) /(x2 –x1) = a;
则:令 (x0 –x1) / (x2 –x1) = a;
计算可得:x0 = a*x2 + (1-a)*x1;
将a带入得到 x0 = [(x0 – x1) / (x2 –x1)]*x2 + [(x2-x0) / (x2 –x1)]*x1;
同理可以得到:y0 = [(y0 – y1) / (y2 – y1)]*y2 + [(y2 – y0) / (y2 – y1)]*y1;
下面我们开始进行双线性插值,如上图2所示,我们需要的想法是先求出R1,R2处的值,再由R1,R2处的值求出P处的值。
对于求解R1,R2处的值,我们可以先进行X方向的插值,在进行Y方向的插值,或者先进行Y方向的线性插值,再进行X方向的线性插值。我采用的是先进行X方向的插值再进行Y方向的插值。具体操作如下:
F(R1) = F(Q11)(x2 - x)/(x2 –x1) + F(Q21)(x – x1)/(x2 –x1);
F(R2) = F(Q12)(x2 - x)/(x2 –x1) + F(Q22)(x –x1)/(x2 –x1);
接着进行Y方向的线性插值:
F(P) = F(R1)(y2 - y)/(y2 – y1) + F(R2)(y –y1)/(y2 – y1);
将F(R1),F(R2)的值带入到上式中可以求得P点处的值。(此处自己演算一下就知道了)
得到了F(P)的表达式,还没完,因为F(P)的实际表达式太复杂,因此我们想到的解决办法是将图二中的4个点Q11,Q12,Q21,Q22映射到(0,0),(0,1),(1,0),(1,1)这四个点处。实际上也就是将此四点的坐标换成(0,0),(0,1),(1,0),(1,1)带入F(P)的表达式中进行计算,之所以可以这样处理的原因在于,我们对某一点的插值实际上关注的是这4点处的函数值。理想中我们认为插值的4点分布在未知点的周围。所以我们构造这样的范围在(0,1)的区域中的四点,对原来的Q11,Q12,Q21,Q22进行映射。不影响对插值点灰度值的计算。带入到表达式之后,我们可以将公式化简为
F(P) = (1-U)(1-V)*F(Q11) + (1-U)*V*F(Q12) + V(1-U)*F(Q21) + U*V*F(Q22);
其中U = X – X1;
V = Y – Y1;
在程序中X1 = floor(X); X2 =ceil(X); Y1 = floor(Y); Y2 = ceil(Y);
第一种插值计算方案求解圆形LBP的代码如下:
void getcicleLbp(const Mat &src, Mat &dst , int neighboors, int radius)
{
if (src.empty())
{
cout << “The image is empty! please check your data!” << endl;
exit(0);
}
Mat gray_image;
if(src.channels() == 3)
{
cvtColor(src,gray_image,CV_BGR2GRAY);
}
else
{
gray_image = src;
}
int rows_num = src.rows;
int cols_num = src.cols;
dst = Mat::zeros(rows_num - radius*2,cols_num - radius*2,CV_8UC1); //这里体现了类型定义的重要性,要是不定义为CV_8UC1,则输出的lbp值会超过255
for(int i = radius; i < rows_num - radius; i++)
{
for(int j = radius; j < cols_num - radius; j++)
{
uchar lbpCode = 0;
uchar center_pix = gray_image.at(i,j);
//注意这里是对gray_image不是src
//求出抽样点的位置
for(int k = 0; k < neighboors; k++)
{
float x =0, y = 0;
x = i + radius*cos(CV_PI*2*k / neighboors);
y = j - radius*sin(CV_PI*2*k / neighboors);
//对坐标点进行双线性插值
int x1 = floor(x); // 向上取整例如x = 0.53 x1 = 0;
int x2 = ceil(x); // 向下取整例如x = 0.53 x2 = 1;
int y1 = floor(y);
int y2 = ceil(y);
/*
利用公式计算双线性插值 f(i+u,j+v) = (1-u)*(1-v)*f(i,j) + (1-u)*v*f(i,j+v) + (1-v)*u*f(i+u,j) + u*v*f(i+u,j+v);
我们以(x,y)为中心,以其他四个点为线性插值的参考点这里的(x,y)就是公式里的
f(i+u,j+v),(x1,y1)就是f(i,j)下面计算u,v实际上我们可以理解为这是将这四点进行了坐标的映射,将四点坐标映射到了[0,1]的矩形空间
*/
float u = x - x1;
float v = y - y1;
//计算相应的权值
float w1 = (1-u)*(1-v);
float w2 = (1-u)*v;
float w3 = (1-v)*u;
float w4 = u*v;
//插值
float nei_value = gray_image.at(x1,y1)*w1 + gray_image.at(x1,y2)*w2
+ gray_image.at(x2,y1)*w3 + gray_image.at(x2,y2)*w4;
// lbpCode |= (center_pix > nei_value) << (neighboors - k - 1);
//得到的是一个数,注意比较关系领域点与中心像素点比较。不要颠倒
lbpCode |= (nei_value > center_pix ) << (neighboors - k - 1);
//得到的是一个数,注意比较关系领域点与中心像素点比较。不要颠倒
}
dst.at(i-radius,j-radius) = lbpCode;
}
}
cv::FileStorage fs(“/tmp/res/lbp/data.xml”,cv::FileStorage::WRITE);
fs <<”circlelbp” << dst ;
fs.release();
if(1)
{
static int cnt = 0;
char file_name[128];
snprintf(file_name,sizeof(file_name),"/tmp/res/lbp/ciclelbp_%d.bmp",++cnt);
easypr::utils::imwrite(file_name,dst);
}
}
为了改进双线性插值计算的速度,我们可以来观察一下公式:
U = X – X1; V = Y – Y1;
其中X = I + R*cos(2*PI*k/P_num);
Y =J – R*sin(2*PI*k/P);
X1 = floor(X) = I + floor(R*cos(2*PI*k/P_num)); Y1 =floor(Y) = J + floor(– R*sin(2*PI*k/P));
所以:U = R*cos(2*PI*k/P) –floor(R*cos(2*PI*k/P_num));
V = – R*sin(2*PI*k/P) - floor(– R*sin(2*PI*k/P));
为了减少双线性插值时计算权值是的计算量,我们分析知道,对于每一个不同的采样点,对其坐标位置产生影响的实际上是由采样半径R与采样间隔引起的,像素的原始坐标对权值没有影响。所以由此分析之后直接计算变化的这一部分,使得权值的计算量相对的减少。
以下是基于此思想的改进代码:值得注意的是,此时我们所定义的ry = -R*sin(2*PI*k / P);因为ry为负数(角度是由0逐渐增加的,由正弦曲线的特性可知道ry为负数),而floor(-1.23) = -2; ceil(-1.23) = -1;所以对于X1,Y1,X2,Y2的定义有所改变,由于图像坐标系的特殊关系,且我们默认Y1 > Y2; 也就是 J + Y1 > J + Y2;而Y1,Y2 为负数。所以需要Y1 > Y2;所以规定Y1 = ceil(ry); Y2 = floor(ry);
以下是改进之后的代码:
void getcircleLbp_anvanced(const Mat &src, Mat &dst,int neighboors, int radius)
{
//cout <<”floor(-1.23)” << “=” << floor(-1.23)<< “\n” << endl; // -2
//cout <<”ceil(-1.23)” << “=” << ceil(-1.23)<< “\n” << endl; // -1
if(src.empty())
{
cout<< "The image is empty! please check your data!" << endl;
exit(0);
}
Mat gray_image;
if(src.channels() == 3)
{
cvtColor(src,gray_image,CV_BGR2GRAY);
}
else
{
gray_image = src;
}
float w1 = 0,w2 = 0,w3 = 0,w4 = 0;
int rx1 = 0,rx2 = 0,ry1 = 0,ry2 = 0;
//先计算进行双线性差值的权值,分析之后可以发现u,v的实际来源在于旋转角度所带来的偏移量
int rows_num = gray_image.rows;
int cols_num = gray_image.cols;
dst = Mat::zeros(rows_num - 2*radius, cols_num - 2*radius, CV_8UC1);
for(auto k = 0; k != neighboors; ++k)
{
float rx = radius*cos(CV_PI*2*k / neighboors);
float ry = -radius*sin(CV_PI*2*k / neighboors); //之所以为负,原因在于图像坐标的情况
rx1 = floor(rx);
rx2 = ceil(rx);
ry1 = ceil(ry); // ry是一个负数,则取得是负数的最小值,ry1在上
ry2 = floor(ry); //
float u = rx - rx1;
float v = ry - ry1;
//计算权值
w1 = (1-u)*(1-v);
w2 = (1-u)*v;
w3 = u*(1-v);
w4 = u*v;
for (int i = radius; i != rows_num - radius; i++)
{
for(int j = radius; j != cols_num - radius; j++)
{
uchar center_pix =gray_image.at(i,j);
//cout <<"center_pix" << "=" << center_pix << endl;
float neighboor = 0;
//进行双线性插值,计算采样点处的灰度值(插值得到)
neighboor = gray_image.at(i+rx1,j+ry1)*w1 + gray_image.at(i+rx1,j+ry2)*w2
+ gray_image.at(i+rx2,j+ry1)*w3 + gray_image.at(i+rx2,j+ry2)*w4;
dst.at(i-radius,j-radius) |= (neighboor > center_pix) << (neighboors - k - 1);
}
}
}
cv::FileStorage fs("/tmp/res/lbp/data_adv.xml",cv::FileStorage::WRITE);
fs <<"circlelbp" << dst ;
fs.release();
if(1)
{
static int cnt = 0;
char file_name[128];
snprintf(file_name,sizeof(file_name),"/tmp/res/lbp/ciclelbp_advance_%d.bmp",++cnt);
easypr::utils::imwrite(file_name,dst);
}
}
(a)原图 (b) 第一种插值 (c)改进插值
(a)原图 (b) 第一种插值 (c)改进插值
3旋转不变模式
所谓的旋转不变模式,实际上是在圆形邻域的基础上产生的。由于圆形邻域中我们又增加了两个变量,那就是半径R和采样点P。将圆形邻域模式的LBP算子记为LBP(P,R)。而对于这种模式的LBP算子,之所以说是圆形邻域,而不是常规的3*3的邻域算子的原因在于,对于一个圆形来讲当图像进行旋转的时候,圆形上的熟知的变化只是0,1序列位置的循环移位,而对于3*3的方形邻域来讲,图像的旋转,带来的不仅是0,1序列位置的变化,还是整体数值的变化,也就是说我们所提出的旋转不变模式是针对多尺度LBP(圆形邻域LBP)来讲的。由于图像的旋转会导致采样点处的编码的变化,导致图片无法识别。因为采样点处的特征点变化了。我们理想中的效果是无论图片是否旋转,图像的特征点不变。为了实现这一目标,我们的想法是对每一个采样点的LBP编码进行循环编码,循环P次,然后对循环后的编码取最小值。将这个最小值对应的模式记为旋转不变模式。之所以取最小值,原因在于减少后续的计算量,实际上取最大或者最小都一样的。只是为了计算的方便。而且若是8个采样点取最小值图像的整体亮度偏低,取最大值图像的整体亮度偏高一点而已。实际上我们希望所得到的数值小一点更好。从代码的实现层面来讲,主要还是要用到C++中的左移和右移操作,将左移和右移操作相结合构成循环左移和循环右移的操作。在我的代码里使用的是循环左移运算;
旋转不变模式的代码实现:在代码实现上特别要注意的一点是,最后的输出图上的值为|=运算一定要注意和一般运算的区别。不要只是=
void GetRotationLbp(const Mat& src, Mat &dst, int neighboors,int radius)
{
if(src.empty())
{
cout<< “The image is empty! please check your data!” << endl;
exit(0);
}
Mat gray_image;
if(src.channels() == 3)
{
cvtColor(src,gray_image,CV_BGR2GRAY);
}
else
{
gray_image = src;
}
int rows_num = gray_image.rows;
int cols_num = gray_image.cols;
dst = Mat::zeros(rows_num - 2*radius,cols_num - 2*radius,CV_8UC1);
for(auto k = 0; k != neighboors; ++k)
{
float rx = radius*cos(CV_PI*2*k / neighboors);
float ry = -radius*sin(CV_PI*2*k / neighboors);
int x1 = floor(rx); //向上取整,就是小于当前值的数,大小比较策略仍然是正常的正负数的比较floor(0.45) = 0;floor(-1.2) = -2;
int x2 = ceil(rx);
int y1 = ceil(ry); //这里之所以写成ceil是由于图像坐标特点,以及双线性差值的顺序,再加上floor()对于负数的作用
int y2 = floor(ry);
//计算双线性插值的权值
//先进行坐标的映射
float u = rx - x1;
float v = ry - y1;
//计算权值
float w1 = (1-u)*(1-v);
float w2 = (1-u)*v;
float w3 = u*(1-v);
float w4 = u*v;
//遍历像素,进行双线性插值和lbp编码
for(auto i = radius; i != rows_num - radius; ++i)
{
for(auto j = radius; j!= cols_num - radius; ++j)
{
uchar center_pix = gray_image.at(i,j);
float nei_value = gray_image.at(i+x1,j+y1)*w1 + gray_image.at(i+x1,j+y2)*w2
+ gray_image.at(i+x2,j+y1)*w3 + gray_image.at(i+x2,j+y2)*w4;
//切记是或等于 |=
dst.at(i-radius, j-radius) |= (nei_value > center_pix) << (neighboors -k -1);
}
}
}
//旋转
for(auto i = 0; i != dst.rows; ++i)
{
for(auto j = 0; j != dst.cols; ++j)
{
uchar current_value = dst.at(i,j);
uchar minValue = current_value;
for(auto k = 1; k != neighboors; ++k) //p种模式中的最小值 k从1开始
{
//循环左移
uchar temp_value = (current_value >> (neighboors - k))|(current_value << k);
if(temp_value < minValue)
{
minValue = temp_value;
}
}
dst.at(i,j) = minValue;
}
}
static int cout = 0;
char file_name[128];
snprintf(file_name,sizeof(file_name),"/tmp/res/lbp/data_rota_%d.xml",cout++);
cv::FileStorage file(file_name,cv::FileStorage::WRITE);
file <<"rotationlbp" << dst ;
file.release();
if(1)
{
static int cnt = 0;
char file_name[128];
snprintf(file_name,sizeof(file_name),"/tmp/res/lbp/ratation_%d.bmp",cnt++);
easypr::utils::imwrite(file_name,dst);
}
}
等价模式
对于等价模式我们最直观的理解那就是使用某些模式来代替2^P的模式。这些模式需要具备一些特点,这些特点由研究人员已经给出了,我们把所有的编码模式中跳变点数(0-1,1-0)小于等于2的这样的一些模式作为一大类,这一类中的每一个模式我们成为等价模式,而将其余的模式归为另一类。这样就将原来的2^P的模式,降维成了P*(P-1) + 2 + 1种模式。以8个采样点为例,就将原来的256种模式降维成了58+1种模式,这58种模式是跳变点个数下雨等于2的那些模式的总数。同时我们将除了这58种模式之外的其他的所有模式归为另一类。记做0模式。这样也就是说我们用59种模式代替了原来的2^P种模式。那为什么我们需要这样做呢?原因在于,对于原始的LBP算子,当我们得到了LBP图像,(对于8位的显示器只能显示8采样点的图像)无论采样点的个数是多少,我们需要对图像进行分块来取每一块的直方图(真实理解直方图的含义,直方图实际上就是一个统计工具,对于常规的图像直方图统计来讲,我们常用的含义统计每一个灰度值上的像素点的个数,直观理解为横坐标是灰度值,纵坐标是像素点的个数,而实际上我们在使用直方图的时候更多的是将它作为一个统计工具,在HOG中,我们以角度为横坐标,像素点个数为纵坐标,在这里的LBP算子中我们以LBP的值(不一定是小于255),为横坐标,以像素点的个数为纵坐标)统计,这样的话,要是每一个块中数据级都是2^P个,那么当采样点个数比较大的时候,我们的数据量会变得很大。这样会消耗掉计算机太多的性能。得不偿失,所以我们需要对数据进行降维。这样就将成级数增加的数据,降维到了相对很少的几种模式了。便于后续的计算。
在这里我最开始一直不明白,为什么总是在强调共有2^P的模式,我在想每一个采样点即使是旋转不变模式,也最多只有P中模式,而总是在讲有2^P的模式,是为什么?后来理解了,我们在这里所说的2^P的模式,是针对整体图像的所有像素点来讲的,每一张图片都有W*H个像素点,这些像素点的LBP值是0–(1111….P)之间的某一个值。也就是说每一点像素的编码值是0到P点全码中的一个,这么多的像素点,2^P个的模式都有可能出现。所以说有2^P的模式是没有问题的。
在旋转不变等价模式的编码过程中,我们需要注意的是,这里涉及到一个对应编码的问题,首先将等价模式的问题进行分解,要实现这样的一个等价模式,我们需要做三件事。1,统计编码的跳变点数。2,进行相应的编码。3,整个等价模式的实现。
首先来看看,编码跳变点数的统计,我们这里采用的输入数据源是旋转不变模式对应的LBP图像。这里我们遇到了一个问题那就是,我们得到的旋转不变模式的图像是一副十进制表示的图像,在统计跳变点的时候,我们需要将这样的值转换为二进制数字来统计,这里二进制的个数是由采样点P的个数控制的。使用到了C++中的类(P).然后遍历转换后的数字,temp[i] ?= temp[(i+1)%P]
接着再来看,相应的编码。我们的编码判定条件是跳变点数最大值为2,而我们编码模式共有2^P个。也就是说我们需要对[0,( (1111…)p -1)]这样范围内的值进行编码,之前有一个顾虑,在实现中我们使用了有个计数标志来进行编码,一直没想明白(以P=8为例),256个值怎么会编码之后就只剩下0—58这59个值呢?而且我们是使用的累加的标志来进行编码的啊。再怎么说255这个数也是等价模式,那他对应的新的编码表不也应该变成了255(因为一直觉得计数标志会一直累加,和循环一样。但是忽略了实际上计数标志的累加是有条件的。而不是每次都随之循环一直加的,在等价模式的条件下,实际上计数标志只加到了58,同时要注意,我们的等价模式是从1开始计数的,也就是说计数标志初始化为1,因为我们将其他的模式归为0,也就是值对应为0),
再来理解一个问题,我们的编码表是对[0,( (1111…)p -1)]这样的每一个值进行了编码。以P = 8为例来讲,我们对0-255编码之后,得到的编码表中的数值实际上只有0-58这59个数。原因是因为这是客观的统计规律。所以后续得出了P*(P-1) + 2个模式的结论。还有一个问题就是,对于我们得到的旋转不变的LBP图像中的每一点的像素值,我们使用等价编码之后的编码值来代替。而不是胡乱的修改。本质上只是使用另外一组编码值来替代当前的像素值。目的是在不影响效果的条件下减少数据量。
代码实现的时候还有一点需要注意一下,那就是如果我们在一份代码里实现等价模式的话,那么我们需要定义一个控制等价模式是否开启的flag.这个flag的控制标志是采样点是否编码完成。因为我们的旋转不变模式,需要找到循环左移或者右移之后的最小值。
代码实现:
void GetRotation_uniform(const Mat& src, Mat &dst, int neighboors, int radius)
{
if(src.empty())
{
cout<< “The image is empty! please check your data!” << endl;
exit(0);
}
Mat gray_image;
if(src.channels() == 3)
{
cvtColor(src,gray_image,CV_BGR2GRAY);
}
else
{
gray_image = src;
}
int rows_num = gray_image.rows;
int cols_num = gray_image.cols;
dst = Mat::zeros(rows_num - 2*radius,cols_num - 2*radius,CV_8UC1);
bool code_flag = false;
for(auto k = 0; k != neighboors; ++k)
{
//对最后一个采样点编码完成之后得到的LBP图像进行等价模式编码
if(k == neighboors - 1)
{
code_flag = true;
}
//首先计算邻域采样点的位置
float rx = radius*cos(CV_PI*2*k / neighboors);
float ry = -radius*sin(CV_PI*2*k / neighboors);
int rx1 = floor(rx);
int rx2 = ceil(rx);
int ry1 = ceil(ry);
int ry2 = floor(ry);
float u = rx - rx1;
float v = ry - ry1;
float w1 = (1-u)*(1-v);
float w2 = (1-u)*v;
float w3 = u*(1-v);
float w4 = u*v;
//圆形邻域
for(auto i = radius; i != rows_num - radius; ++i)
{
for(auto j = radius; j != cols_num -radius; ++j)
{
uchar center_pix = gray_image.at(i,j);
uchar nei_value = 0;
nei_value = gray_image.at(i+rx1,j+ry1)*w1 + gray_image.at(i+rx1,j+ry2)*w2
+ gray_image.at(i+rx2,j+ry1)*w3 + gray_image.at(i+rx2,j+ry2)*w4;
dst.at(i-radius,j-radius) |= (nei_value > center_pix) << (neighboors - k -1);
}
}
}
//旋转不变
for(auto i = 0; i != dst.rows; ++i)
{
for(auto j = 0; j != dst.cols; ++j)
{
uchar cur_value = dst.at(i,j);
uchar minValue = cur_value;
for(auto k = 1; k != neighboors; ++k)
{
uchar temp_value = (cur_value >> (neighboors -k))|(cur_value << k);
if(temp_value < minValue)
{
minValue = temp_value;
}
}
dst.at(i,j) = minValue;
}
}
//等价模式编码
uchar pattorn = 1;
uchar code_table[256] = {0};
for(int i = 0; i < 256; i++)
{
//统计跳变点数
int count = 0;
bitset<8> binaryCode = i;
for(int m = 0; m < 8; m++)
{
if(binaryCode[m] != binaryCode[(m+1)%8])
{
count++;
}
}
if(count < 3)
{
code_table[i] = pattorn;
pattorn++;
}
else
{
code_table[i] = 0;
}
}
//等价模式编码
if(code_flag == true)
{
for(auto i = 0; i != dst.rows; ++i)
{
for(auto j = 0; j != dst.cols; ++j)
{
dst.at(i,j) = code_table[dst.at(i,j)];
}
}
}
if(1)
{
static int cnt = 0;
char file_name[128];
snprintf(file_name,sizeof(file_name),"/tmp/res/lbp/uniform_%d.bmp",cnt++);
easypr::utils::imwrite(file_name,dst);
}



