CS231n笔记(1)线性分类器
主要关于lecture 2,只记录贫僧觉得有用的东西,所以课程里一些介绍性的内容会被忽略掉。
图片分类
图片分类就是输入一张图片,然后将这张图片归为确定的类别中的一类。大部分看起来不像是图片分类的机器视觉任务其实可以通过图片分类来完成。
图片分类的例子:
对上面这张 248×400×3 248 × 400 × 3 的矩阵进行分类,将这张图片归类为{猫, 狗, 帽子, 杯子}中的某个类别。
图像识别的难题:
- 视角变化(Viewpoint variation)
- 大小变化(Scale variation)
- 变形(Deformation)
- 对象只有一小部分出现在图片中(Occlusion)
- 光照问题(Illumination conditions)
- 环境背景干扰(Background clutter)
- 同类别的不同形态(Intra-class variation)
因为直接通过编程方式来识别图像太麻烦了,所以要通过数据驱动的方式来让程序自己学会怎么识别。
数据驱动方式:
- 收集一大堆带有标签的图片(标签是人工标注的,所以给这种方法带来了一定的局限性)(就像下图那样的图片集)
- 用机器学习算法训练分类器
- 在新图片上评估分类器的性能
NN(最近邻)分类器
最简单的:NN(Nearest Neighbor),训练出来的分类器会直接记忆每张图片,然后在预测时挑最相似的图片(但是性能不怎么样,分类结果也不是很准确)。
图像分类用到的数据集例子:CIFAR-10。这个数据集含有60000张图片,每张图片是 32×32 32 × 32 像素的。并且每张图片属于10个类别中的一种(已经被附上标签了),其中50000张用来训练,10000张用来测试。
CIFAR-10中的样图,左边是训练集图片,右边是测试集图片:
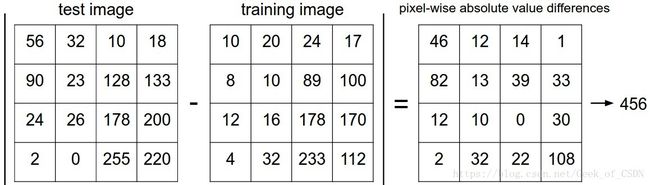
L1距离: d1(I1,I2)=∑P∣∣IP1−IP2∣∣ d 1 ( I 1 , I 2 ) = ∑ P | I 1 P − I 2 P |
NN里面就是用了L1距离来计算两张图片之间的差异,下图是个计算的例子:
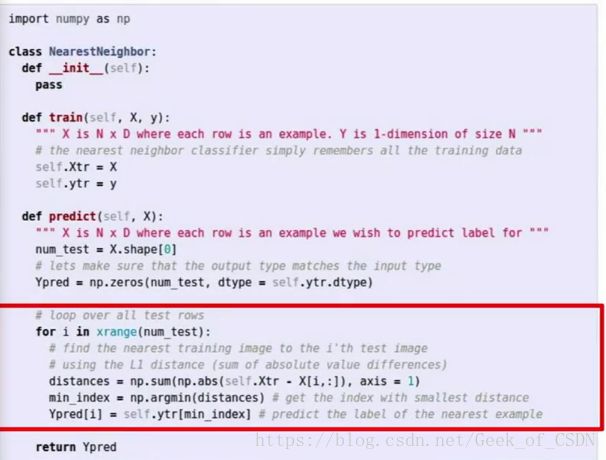
ppt上面的程序例子:
上面红框圈出来的部分就是L1距离。上面的程序片段主要有两个部分,训练(train)和预测(predict),之后写的大部分程序也都会是分成这两个部分。
ppt上程序文字版:
import numpy as np
class NearestNeighbor(object):
def __init__(self):
pass
def train(self, X, y):
""" X是N x D大小,每行是张图片。Y是1 x N,象征输出的类别 """
# NN分类器直接记住了所有的训练数据
self.Xtr = X
self.ytr = y
def predict(self, X):
""" X是N x D大小,其中的每行是我们希望预测的标签的示例 """
num_test = X.shape[0]
# 确保输出类型与输入类型一样
Ypred = np.zeros(num_test, dtype = self.ytr.dtype)
# 在所有测试行上面循环
for i in xrange(num_test):
# 找到所有与训练图片具有最短L1距离的测试图片
distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
min_index = np.argmin(distances) # get the index with smallest distance
Ypred[i] = self.ytr[min_index] # predict the label of the nearest example
return Ypred但是在直接使用上面的代码之前先要将图片转化成一行的矩阵:
Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magic function we provide
# flatten out all images to be one-dimensional
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072下面是训练和predict的代码:
nn = NearestNeighbor() # 创建NN分类器类
nn.train(Xtr_rows, Ytr) # 在训练图像和标签上训练分类器
Yte_predict = nn.predict(Xte_rows) # 在测试图像上predict对应的标签
# 打印出分类的精度(平均数)(用predict出的标签和实际标签比较来得出精度)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )NN不是一个好算法,因为虽然它的train复杂度很低(只需要直接记住每一张训练用的图片),但是它的predict复杂度很高(因为要拿要预测类别的图片和所有训练用的图片进行比较),所以在predict的时候运行速度会很慢(我们通常希望的是predict过程很快,而且对predict进行的平台的性能要求不高,训练速度通常没有太大的要求,当然也不能太慢。这是因为通常训练是在大型的数据中心里面训练的,而predict的时候可能会在用户的手机上跑predict)。
最后的精度大概在38.6%左右,比随机地猜类别效果好一点,而人类的精度在94%左右,最新的CNN已经到了95%左右。
在分类中的效果示意图:
除了上面的L1距离之外还可以选择L2距离:
选择了L2距离的话就要把上面代码里面的distances改成:
distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))L2距离的NN分类器在CIFAR-10上的精度大概在35.4%上。
L1和L2距离是最常用的p-norm距离。
KNN
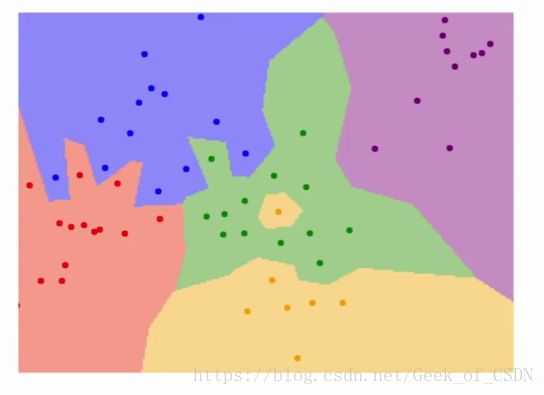
为了改进提出了KNN算法,算法会根据根据某个区域附近的k个点来确定这个区域应该分成哪个类别:
上面的白色区域代表这些区域附近没有足够的点来确定属于哪个区域,其实可以强行归类,但是通常只是留着。注意上面的图里面在K是1的时候中间的那一片黄色区域,这片黄色区域可能是错误分类的区域,而在K等于3、5的时候这篇区域消失了,模型表现出了更加好的泛化能力(generalization)。
KNN算法是最基础的算法,相关的知识将会在神经网络里面用到(了解基本思路就可以了,不用深究程序实现方式,程序要慢慢来)。
检验集
除了L1、L2之外还有很多种的距离函数可以选择,这些选择就叫做超参数(hyperparameters)。不能够直接在测试集上面调模型的超参数(不然可能会出现过拟合现象。测试集不论在什么时候都应该是当作未知的新数据使用,即只能够在模型训练好之后才使用),所以只能够另外分出个检验集,然后让模型在这上面调整超参数。最后才使用测试集来测试模型的泛化能力。
在CIFAR-10里可以这么做:49000张图片作为训练集,1000张图片作为验证集:
# 假设我们像以前一样有Xtr_rows,Ytr,Xte_rows,Yte
# Xtr_rows是50,000 x 3072矩阵
Xval_rows = Xtr_rows[:1000, :] # take first 1000 for validation
Yval = Ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :] # keep last 49,000 for train
Ytr = Ytr[1000:]
# 找到在验证集上最有效的超参数
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:
# 设定k并在验证数据上进行评估
nn = NearestNeighbor()
nn.train(Xtr_rows, Ytr)
# 下面是一个更改了的NearestNeighbor类,能够接受k作为输入
Yval_predict = nn.predict(Xval_rows, k = k)
acc = np.mean(Yval_predict == Yval)
print 'accuracy: %f' % (acc,)
# 追踪在验证集上运行的效果
validation_accuracies.append((k, acc))最后的训练过程可以总结成:
将训练集分成训练和验证集合。用验证集来调超参数。在最后的时候在测试集上跑来看模型性能。
交叉验证:当你的数据比较小的时候可以用交叉验证来确定最终的超参数。方法是将数据集随机地分成几个部分,然后在训练集上训练模型,在验证集上验证(训练一次验证一次,最后再算出一个平均的),最后在测试集上测试模型性能。
实际应用中因为交叉验证计算量比较大,所以通常人们更加喜欢单独设定某部分数据专门用来做验证而不是对整个数据集进行拆分。通常会将原本的训练集中的50%~90%分作训练,剩下的用来验证。如果数据集小的话采用交叉验证,通常是3、5、10等份来分。
下图是将原训练集进行了5等份分割,一部分作为交叉验证用的验证集:
线性分类器
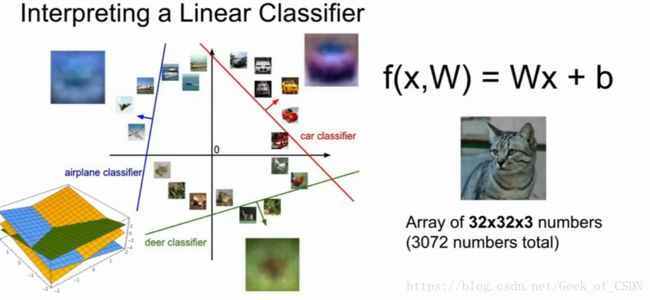
可以设计一种和下图一样的简单线性分类器,输入 x x 是图片(其实可以不只是图片,用文字之类的也行,但是这里举图片的例子更加方便理解),分类器就是那个映射 f f 。权重 W W (注意是矩阵)将会与输入的像素的值(总共3072个值,是矩阵)进行运算(这里是矩阵乘,由映射 f f 决定),最终输出10个数字来决定这张图片对应的类别是什么。
有时会加上偏置值,这个值不会与训练数据有直接相关的运算(如矩阵乘),而是在权重与训练数据运算后加上去的。这个值用来进行对某一类别的偏好进行调整。
例子:当你的训练数据里面猫的类别比狗的类别数量多的时候那么可能偏置值里面的猫对应的类别的偏置会比狗的偏置要高。
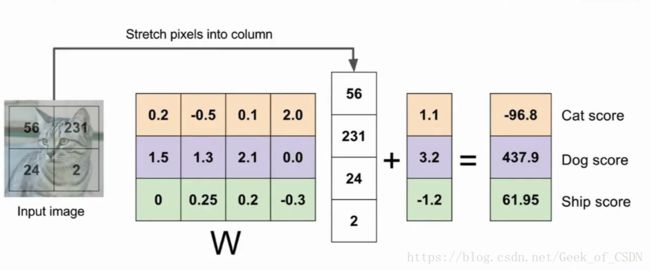
一个更加具体的例子:
线性分类器就像是在一个高维平面上画直线(其实可以这样想,最终公式可以化简成线性的 kx+b k x + b ),然后根据输出来决定输入图片的类别。
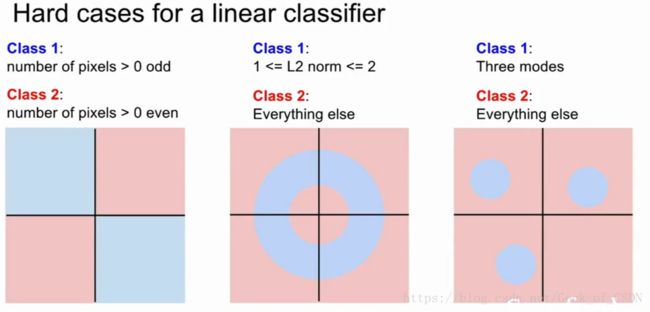
这就会出现一个问题,如果要分类的对象无法用一条直线来划分开的话线性分类器就没有用了。
另一种情况就是多分类的情况,线性分类器也没办法在这种情况下好好工作。
参考
CS231n官网,万恶之源
斯坦福深度学习课程CS231N 2017中文字幕版+全部作业参考