KMP算法笔记(C++)
要搞懂KMP算法首先要明白这个算法是用来做什么的。
需求
无耻的熟人xx:“欸~小上官,原来你(也)是个程序员,那帮我想想看……”
你:S.x.x.T,我连自己的内心活动都自带哔哔声和谐了,你还要我搞什么!
伟大的朋友xx:“……怎么从一串字符串里面搜索出想要的子串。搞得好的话……”,说着就掏出了手机打开了苇名城的信,“把她/他介绍给你。”
你:“我不是那种人。”
高尚的好友xx:“加上这个。”
你:“这不太好。”
高尚无私且伟大的同志xx:“再加上这个。”
你:
“私聊。”
果然无人能抵抗苇名城的魅力。
回到正题,KMP算法可以用在查找字符串中的子串,即匹配字符串。什么是字串?例如“believe”中就有“lie”、“bitch”里面有“bit”,“lie”、“bit”就是子串,“believe”、“bitch”就是主串。我们定义子串在主串中的位置就是子串的第一个字符在主串中的序号。不过老婆/公饼里面真的没老婆/公。
在真的开始讲KMP之前我们先看下暴力解法。
暴力解法
class Solution {
public:
int strStr(string haystack, string needle) {
if(needle.empty())
return 0;
int i=0,j=0;
while(haystack[i]!='\0'&&needle[j]!='\0')
{
if(haystack[i]==needle[j])
{
i++;
j++;
}
else
{
i=i-j+1;
j=0;
}
}
if(needle[j]=='\0')
return i-j;
return -1;
}
};
上面这部分代码的作者是2227。haystack是主串,needle是子串,
其实这个算法叫BF算法(Brute Force)。原理很简单,就是每次子串和主串发现不匹配,那么将子串往前移一格,直到匹配或者移出边界为止。
这种算法的弊端在于,有些时候没有必要只移动一格,例如,当子串为aaab,主串为abcdefgaaab的时候,如果每次都只移动一格,那么就需要移动7格才可以找到匹配的字符串(从abcd。。。一直移动到aaab的a处)。
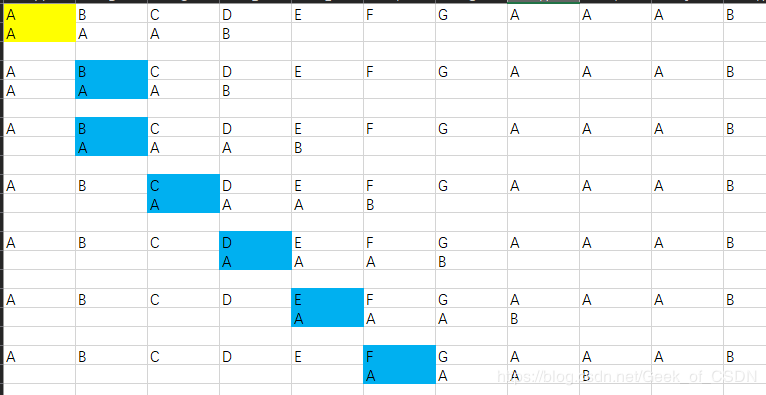
画图太麻烦,所以我用了excel来代替,只做出了前面几个步骤,后面太麻烦就当不存在好了。
那么如果每次直接移动4格呢(aaab总共有四个,即每次移动子串的长度)?这样虽然可能会快一点到达匹配的字符串附近,但是大部分时候会直接越过要匹配的目标。
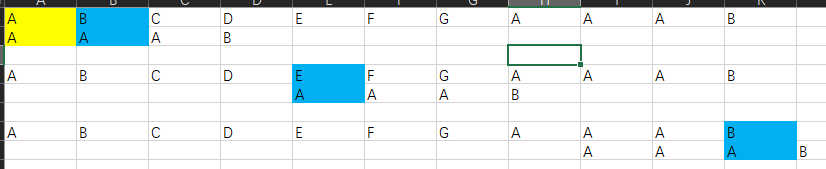
所以,我们就需要找到一个折中而且更灵活的方案(别和我说每次跳1/2子串长度,这样一样会出问题)。
某小布尔乔亚:“更加灵活的方案?那么如果每次跳转随机个长度呢?”
上面这个人 已经凉了,尚存的体温潺潺地从他破碎的躯体中流出,飘散在茫茫雪原上。雪原,在短暂的喧嚣后又恢复了以往的寂静。过不了多久,这里便要恢复纯净,仿佛自太初以来便保持着一贯的清纯。徒留下皑皑白骨,无声地细语着曾经的暴行。果然,世上没有救世主,将生命交给命运的人,得到的只有残羹与绝望。
不过这给了我们一个思路,那就是,每次推进的格数不一定要一样。
那么,我们假设有这么个数组next,用来记录每次不匹配时应当返回的下标,怎么确定这个数组里面的数值(相当于每次不匹配时应推进多少格)?这里补充几点说明:我们假设有两个指针,指针i指向主串的元素,指针j指向子串的元素,我们就是通过控制指针i和j的指向来实现“子串推进”的。
首先我们看到,我们之前的策略,无论是只前进一格还是每次前进子串长度个格,依据的都是子串本身。这是因为,首先,在实际应用中我们不可能预先知道主串的分布是怎么样的,只能够知道子串是怎么样的(例如用户输入了一段字符串,搜索引擎要根据这段字符串去找匹配的搜索结果,因为可能有些页面内容会发生改变,有些网站可能突然宕机了无法访问或者干脆就是被“因为众所周知的原因”了,所以主串具体是怎么样的我们没办法知道);其次,其实该移动多少位是由子串决定的,下面我们分析下为什么这样。
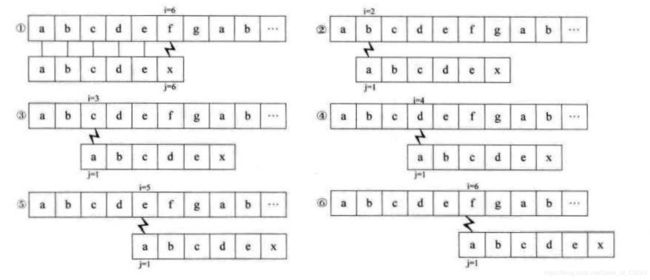
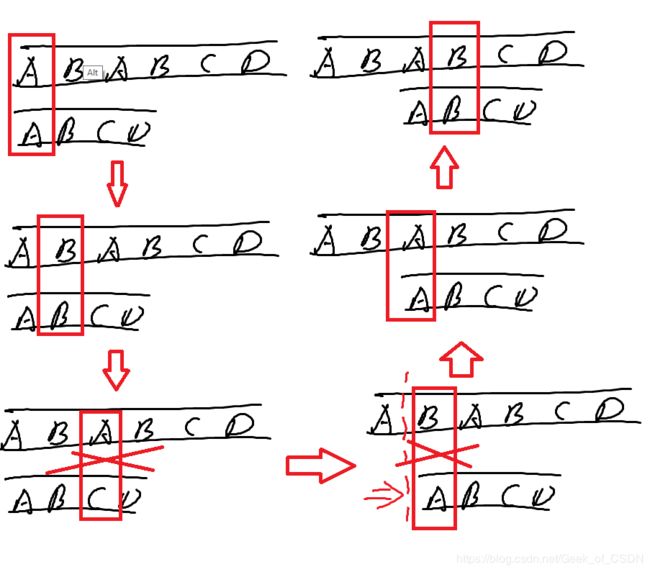
先放上一张来自《大话数据结构》的图。上图中是使用最开始的BF算法的步骤。
我们可以发现,其实步骤2~5是多余的,因为子串中第0个字母a和后面的bcdex都不相同,那么当第5位的x发生不匹配的时候,可以确定主串中的第1位到第4位都不可能和子串的a相对应。因此我们得出这么个结论,我们可以通过观察子串本身来确定每次不匹配发生的时候该移动子串多少格。
在确定之前我们先介绍一个概念,前缀和后缀。例如上图中的子串abcdex,前后缀为:
| 模式串的各个子串 |
前缀 | 后缀 | 最大公共元素长度 |
|---|---|---|---|
| A | 空 | 空 | 0 |
| AB | A | B | 0 |
| ABC | A, AB | C, BC |
0 |
| ABCD | A, AB, ABC | D, CD, BCD | 0 |
| ABCDE | A, AB, ABC, ABCD | E, DE, CDE, BCDE | 0 |
| ABCDEX | A, AB, ABC, ABCD, ABCDE | X, EX, DEX, CDEX, BCDEX | 0 |
最大公共元素就是例如,字串为aaab,那么最后一个a的前缀有:a, aa,后缀有a, aa,所以最大公共元素为2(aa有两个元素,a和a)。
通过上面的表格我们可以得到abcdex的next数组是-1, 0, 0, 0, 0, 0。即,每次不匹配发生的时候都要返回到下标0,a的位置(next的内容是每次不匹配发生的时候返回的下标,这里我们的假设有两个指针分别指向主串和子串)。最开始的元素对应的next下标定为-1,因为我们默认当j为-1时i和j都往后移动一格(即将子串整体往右移动一格,移动后j为0,指向第0位元素,i指向下一个元素)。
所以我们可以知道next数组的生成方式就是:
- 选定某个元素
- 对比这个元素的前缀和后缀,最大公共元素数就是这个元素对应的发生不匹配时要跳转的下标
- 将这个要跳转的下标填入next数组中,并如此循环,直到确定所有元素对应的跳转下标
至于为什么这么做呢?这里引用下KMP ~~从入门到理解到彻底理解里面的内容。重点是失配后能够确定前面多少个字符是有用的。
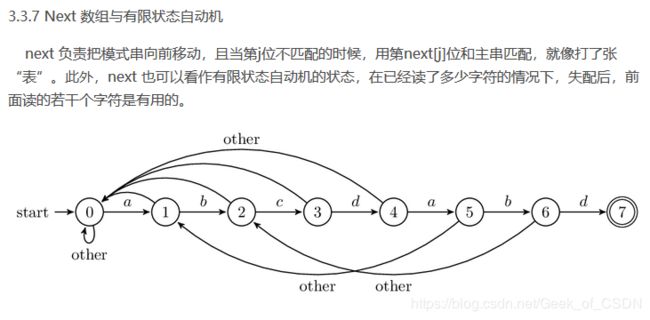
那为什么next数组能确定之前有多少个字符是有用的?因为通过比对前缀和后缀我们可以确定哪个前缀会对后面的判断有影响,这是因为后缀中已经出现了与前缀一样的组合,所以没有必要重复尝试匹配前缀,所以当不匹配发生的时候只需要重新跳转回对应的前缀即可(即跳转回前缀对应的下标)。
next数组的生成
那么具体怎么生成next数组呢?
vector getNext(string pattern){
vector next;
int j = -1;
int i = 0;
int len = pattern.size();
next.push_back(-1);
while(i 解释下上面的程序,其实原理很简单,首先我们默认第一个元素对应的next为-1。其他的就是尽量寻找最长的匹配的前缀,具体操作就是如果当前元素和前一个前缀的最后一个元素(j对应的部分)相同,那么可以确定下一个元素对应的最长匹配的前缀为之前的前缀和它后面一个元素的组合。例如aaab,最后一个a(第2位元素)的处理过程是,i=1,j=0,因为第1位和第2位(0开始的下标)元素相同,所以对应的最长前缀是1位(0~1的组合,即aa为对应的前缀,跳转的时候只需要跳转到前缀最后一个元素对应的位置即可避免重复匹配)。如此类推。
这是还没经过优化的KMP算法,如果优化过的话那么:
vector getNext(string pattern){
vector next;
int j = -1;
int i = 0;
int len = pattern.size();
next.push_back(-1);
while(i 多了一个判断,因为如果当前元素和前一个元素一样,那么当前元素不匹配的时候前一个元素肯定也不匹配,所以应当返回到前一个元素对应的前缀。
组合起来
那么具体怎么实现字符串的匹配呢?这里以LeetCode的28号题目为例子:
class Solution {
public:
int strStr(string haystack, string needle) {
if(needle.empty()){
return 0;
}
vector next;
int i = 0;
int j = 0;
int sLen = haystack.size();
int tLen = needle.size();
next = getNext(needle);
while((i getNext(string pattern){
vector next;
int j = -1;
int i = 0;
int len = pattern.size();
next.push_back(-1);
while(i 简单说就是主串和子串比对(这里和BF是一样的),当发生不匹配的时候才访问next数组然后获取子串要定位的下标。
参考
《大话数据结构》
KMP ~~从入门到理解到彻底理解