机器学习之统计和概率论

一、基本数学概念

其中四分位数通常用以判断数据集中的异常值。

偏态和峰态可用于判断该分布是不是正态分布。

二、概率分布

概率分布分为离散概率分布和连续概率分布，在python中通过scipy.stats库实现。

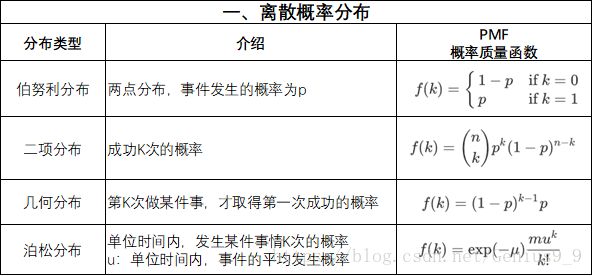
  离散概率分布：PMF概率质量函数

  连续概率分布：PDF概率密度函数

详情参阅官方文档：https://docs.scipy.org/doc/scipy/reference/stats.html

1. 离散概率分布

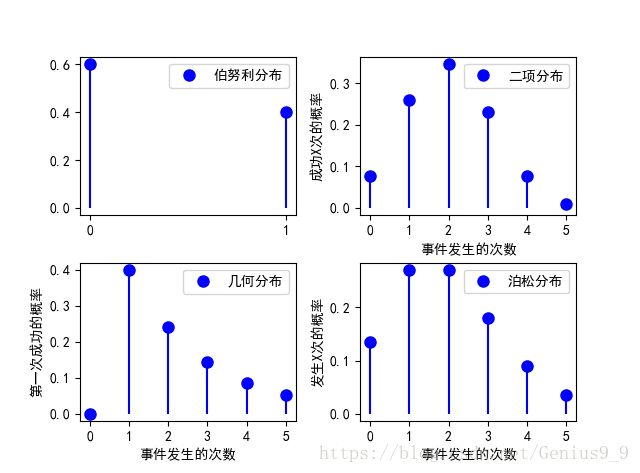
通过python实现各分布的绘制：

实现代码如下：

import scipy.stats as ss
import numpy as np
import matplotlib.pyplot as plt
from pylab import *


if __name__ == '__main__':
    mpl.rcParams['font.sans-serif'] = ['SimHei']
    #p表示事件发生的概率
    #n表示做某件事情的次数
    n=5
    p = 0.4
    X = np.arange(0, n + 1, 1)
    fig,axes = plt.subplots(2, 2)

    #1.绘制伯努利分布
    #k=1，事件发生；k=0，事件不发生；
    k=np.arange(0,2,1)
    ber=ss.bernoulli.pmf(k,p)
    axes[0,0].plot(k,ber,'bo',ms=8,label='伯努利分布')
    #绘制直线
    axes[0,0].vlines(x=    k, ymin = 0, ymax = ber, colors = 'b')
    axes[0, 0].legend(loc='upper right')
    axes[0, 0].set_xticks(k)

    #2.绘制二项分布
    binom=ss.binom.pmf(X,n,p)
    axes[0,1].plot(X,binom,'bo',ms=8,label='二项分布')
    axes[0,1].vlines(x=X,ymin=0,ymax=binom,colors='b')
    axes[0,1].legend(loc='upper right')
    axes[0,1].set_xticks(X)
    axes[0,1].set_xlabel('事件发生的次数')
    axes[0,1].set_ylabel('成功X次的概率')

    #3.绘制几何分布
    geom=ss.geom.pmf(X,p)
    axes[1,0].plot(X, geom, 'bo', ms=8, label='几何分布')
    axes[1,0].vlines(x=X, ymin=0, ymax=geom, colors='b')
    axes[1,0].legend(loc='upper right')
    axes[1,0].set_xticks(X)
    axes[1,0].set_xlabel('事件发生的次数')
    axes[1,0].set_ylabel('第一次成功的概率')

    #4绘制泊松分布
    mu=2
    pois=ss.poisson.pmf(X,mu)
    axes[1, 1].plot(X, pois, 'bo', ms=8, label='泊松分布')
    axes[1, 1].vlines(x=X, ymin=0, ymax=pois, colors='b')
    axes[1, 1].legend(loc='upper right')
    axes[1, 1].set_xticks(X)
    axes[1, 1].set_xlabel('事件发生的次数')
    axes[1, 1].set_ylabel('发生X次的概率')

    plt.subplots_adjust(left=None, bottom=None, right=None, top=None,
                    wspace=0.3, hspace=0.3)
    plt.show()

二、连续概率分布

下一篇文档更新。