案例解释图像傅里叶变换的幅度谱和相位谱的以及反变换
目的:读取图像 A(lena.tiff)和B(rice.tif),显示这两幅图像,对图像作傅立叶变换,显示图像的傅里叶幅度谱和相位谱。做傅立叶逆变换,显示重建图像。
图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度
对图像而言,图像的边缘部分是突变部分,变化较快,因此反应在频域上是高频分量(能量低,在变换后的图中,呈现黑灰色,内容见我的上一篇博客http://blog.csdn.net/goodshot/article/details/78488459);图像的噪声大部分情况下是高频部分;图像平缓变化部分则为低频分量(能量高,在变换后的图中,呈现黑灰色)。也就是说,傅立叶变换提供另外一个角度来观察图像,可以将图像从灰度分布转化到频率分布上来观察图像的特征。
imshow()函数:
imshwo()函数用于接收一个像素矩阵,显示该图像,其显示的参数有两种类型
unit8;像素在矩阵处理范围为0-255
double:若值大于1,转化为1,若小于1,转化为0
图像进行二维傅立叶变换得到频谱图,就是图像梯度的分布图,当然频谱图上的各点与图像上各点并不存在一一对应的关系,即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点,实际是图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点的频率(关于频率,参考后面的附文)的大小(可以这么理解,图像中的低频部分(能量大,呈现白色)指低梯度的点,高频部分相反(能量小,呈现黑灰色))。
代码如下:
%%图像的傅里叶变换%%
imA=imread('rice.tif','tif'); %读取图像
imB=imread('lena.tiff','tif');
subplot(2,3,1);
imshow(imA);
title('原图像A');
subplot(2,3,2);
imshow(imB);
title('原图像B');
FA=fft2(imA);%对图像进行傅里叶变换
FB=fft2(imB);
fA=fftshift(FA); %对图像频谱进行移动,是0频率点在中心
fB=fftshift(FB);
sA=log(abs(fA));%获得傅里叶变换的幅度谱
sB=log(abs(fB));
phA=log(angle(fA)*180/pi);%获得傅里叶变换的相位谱
phB=log(angle(fB)*180/pi);
subplot(2,3,3);
imshow(sA,[]); %显示图像的度谱,参数与[]是为了将sA的值线形拉伸
title('图像A的傅里叶变换幅度谱');
subplot(2,3,4);
imshow(phA,[]); %显示图像傅里叶变换的相位谱
title('图像A傅里叶变换的相位谱');
subplot(2,3,5);
imshow(sB,[])
title('图像B的傅里叶变换幅度谱');
subplot(2,3,6);
imshow(phB,[]);
title('图像B傅里叶变换的相位谱');
A=ifft2(FA);%傅里叶反变换
B=ifft2(FB);
figure
subplot(1,2,1);
imshow(A,[]);
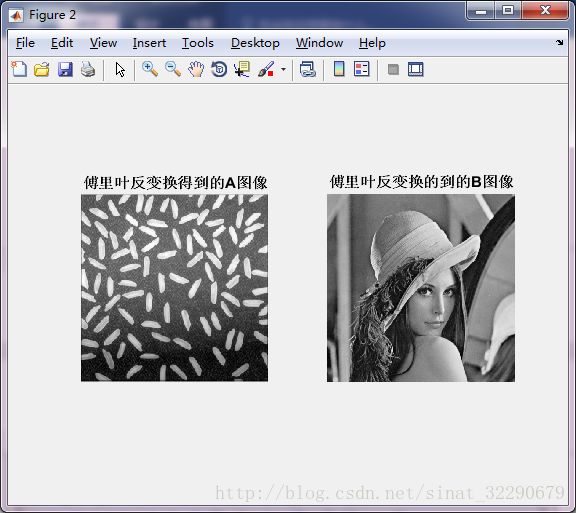
title('傅里叶反变换得到的A图像');
subplot(1,2,2);
imshow(B,[]);
title('傅里叶反变换的到的B图像');
附:
角速度和角频率是同一个物理量吗?
2012-02-03 09:37阅读:4,830
与哪些因素有关 与物体所受向心力有关 只由振动系统本身性质决定与速度的关系 ω = v/r ( v为线速度) v = ωasin(ω t + φ ) (a为振幅) 我们往往在分析简谐振动时,采用参考圆法,那么参考点以角速度ω旋转时,它的投影就代表了给定的简谐振动的位移规律.这时参考点的角速度跟振动的角频率相对应.应该指出,用参考圆研究简谐振动仅仅只是一种方法,两种运动是不同性质的机械运动,它们之间没有什么必然的联系.