GAN的基本原理

---

GAN 简介

GAN的工作原理

generator 和 discriminator相互博弈：

• discrimiator最大化真实样例与generator样例之间的差异
• generator根据discriminator“反馈的指导信息”，更新参数，生成“更靠谱”的样例，减小与真实样例的差异。

Minimax Game:

minGmaxDV(G,D) m i n G m a x D V ( G , D )

在origin GAN中：

V=Ex∼Pdata[logD(x)]+Ex∼PG[log(1−D(x))] V = E x ∼ P d a t a [ l o g D ( x ) ] + E x ∼ P G [ l o g ( 1 − D ( x ) ) ]

一般而言，G是neural network, 它从一个先验分布 Pz P z ,生成x,上式写成：

V=Ex∼Pdata[logD(x)]+Ez∼Pz[log(1−D(G(z)))] V = E x ∼ P d a t a [ l o g D ( x ) ] + E z ∼ P z [ l o g ( 1 − D ( G ( z ) ) ) ]

GAN的应用示例

目前，Tensorflow 1.4已经提供了一些gan的实现，在tf.contrib.gan中；另外，有很多开源的GAN的实现。（示例略，可以参加mnist上的各种实验和DCGAN、WGAN等生成的图片）

GAN与ML

LR判别模型

样本实例集合： D={(xi,yi)}ni=1 D = { ( x i , y i ) } i = 1 n
利用最大似然(ML), 求解判别模型： hθ(x)=11+e−θTx h θ ( x ) = 1 1 + e − θ T x

θ∗=arg max 1n∑i=1nyilog hθ(xi)+(1−yi)log(1−hθ(xi))=arg max 1n∑yi=1log hθ(xi)+∑yj=0log(1−hθ(xj))=arg max |D1|n1|D1|∑D1log hθ(xi)+|D0|n1|D0|∑D0log hθ(xj)=arg max P(y=1)Ex∼P(x|y=1)[loghθ(x)]+P(y=0)Ex∼P(x|y=0)[log(1−hθ(x))] θ ∗ = a r g   m a x   1 n ∑ i = 1 n y i l o g   h θ ( x i ) + ( 1 − y i ) l o g ( 1 − h θ ( x i ) ) = a r g   m a x   1 n ∑ y i = 1 l o g   h θ ( x i ) + ∑ y j = 0 l o g ( 1 − h θ ( x j ) ) = a r g   m a x   | D 1 | n 1 | D 1 | ∑ D 1 l o g   h θ ( x i ) + | D 0 | n 1 | D 0 | ∑ D 0 l o g   h θ ( x j ) = a r g   m a x   P ( y = 1 ) E x ∼ P ( x | y = 1 ) [ l o g h θ ( x ) ] + P ( y = 0 ) E x ∼ P ( x | y = 0 ) [ l o g ( 1 − h θ ( x ) ) ]

事实上，当假设空间 hθ(x) h θ ( x ) 有足够强的表征能力，（比如真实分布确实由LR模型生成，或者 hθ h θ 是深层神经网络，可以表征任意函数）；通过求导，可以得到最优解为：

h∗θ(x)=P(y=1)P(x|y=1)P(y=1)P(x|y=1)+P(y=0)P(x|y=0)=P(x,y=1)P(x)=P(y=1|x) h θ ∗ ( x ) = P ( y = 1 ) P ( x | y = 1 ) P ( y = 1 ) P ( x | y = 1 ) + P ( y = 0 ) P ( x | y = 0 ) = P ( x , y = 1 ) P ( x ) = P ( y = 1 | x )

(额，貌似推理了一句废话，不过这个公式正说明，当我们采用ML或者cross entropy的时候，最优解正是后验概率（条件概率），前提是 hθ(x) h θ ( x ) 有足够强的表征能力。推导这个式子，也可以和后面推导 D∗ D ∗ 相互验证)
观察式子：

• xi x i 是正例， hθ(xi) h θ ( x i ) 尽可能大，接近1
• xj x j 是负例， hθ(xj) h θ ( x j ) 尽可能小，接近0
• 或者添加负号，可以从极小化negative log loss的角度考虑。

对于GAN而言，某种程度上，D是h:

• xi∼Pdata x i ∼ P d a t a , 是“正例”，判别器D应使得 D(xi) D ( x i ) 尽可能大，接近1，即极大化 log(D(xi)) l o g ( D ( x i ) )
• xj∼PG x j ∼ P G , 是“负例”，判别器D应使得 D(xj) D ( x j ) 尽可能小，接近0, 即极大化 log(1−D(xj)) l o g ( 1 − D ( x j ) )
• 类似地，忽略先验概率，V函数定义为
  V=Ex∼Pdata[logD(x)]+Ex∼PG[log(1−D(x))]=Ex∼Pdata[logD(x)]+Ez∼Pz[log(1−D(G(z)))] V = E x ∼ P d a t a [ l o g D ( x ) ] + E x ∼ P G [ l o g ( 1 − D ( x ) ) ] = E x ∼ P d a t a [ l o g D ( x ) ] + E z ∼ P z [ l o g ( 1 − D ( G ( z ) ) ) ]
  , 而 D∗=maxDV(G,D) D ∗ = m a x D V ( G , D ) ; （这里忽略 P(y) P ( y ) ,两类先验概率相等，正对应后面训练D时，进行相等数量的sample）

事实上，训练判别器D的过程，正是使用ML求解二分类问题：

• sample x1,x2⋯xn x 1 , x 2 ⋯ x n from Pdata(x) P d a t a ( x ) , 作为正例
• sample x1~,x2~⋯xn~ x 1 ~ , x 2 ~ ⋯ x n ~ from PG(x) P G ( x ) （实际是sample z）， 作为负例
• 利用最大似然求解 V=1n∑ni=1log D(xi)+1n∑ni=1log(1−D(x̃ i)) V = 1 n ∑ i = 1 n l o g   D ( x i ) + 1 n ∑ i = 1 n l o g ( 1 − D ( x ~ i ) )

(同样的思想，有“NCE”， “negative sampling”)

ori-GAN和ML分别衡量不同的divergency

• ML 衡量生成模型与真实概率分布的KL距离
• ori-GAN衡量JS距离

ML and KL divergency

未知的真实分布： Pdata(x) P d a t a ( x )
样本实例集： D={xi}ni=1 D = { x i } i = 1 n ， 采样自 Pdata(x) P d a t a ( x )
假设空间中的生成模型： PG(x;θ) P G ( x ; θ ) 来模拟 Pdata(x) P d a t a ( x )
根据ML原则：

θ∗=argmaxθ∏i=1nPG(xi;θ)=argmaxθ1n∑i=1nlog PG(xi;θ)≈argmaxθEx∼Pdata[logPG(x;θ)]=argmaxθ∫xPdata(x)logPG(x;θ)dx−∫xPdata(x)logPdata(x)dx=argminθKL(Pdata(x) || PG(x;θ)) θ ∗ = a r g m a x θ ∏ i = 1 n P G ( x i ; θ ) = a r g m a x θ 1 n ∑ i = 1 n l o g   P G ( x i ; θ ) ≈ a r g m a x θ E x ∼ P d a t a [ l o g P G ( x ; θ ) ] = a r g m a x θ ∫ x P d a t a ( x ) l o g P G ( x ; θ ) d x − ∫ x P d a t a ( x ) l o g P d a t a ( x ) d x = a r g m i n θ K L ( P d a t a ( x )   | |   P G ( x ; θ ) )

所以，对生成模型采用ML原则，实际最小化KL距离。

origin-GAN and JS Divergency

1. 给定G, 求解 D∗=maxDV(G,D) D ∗ = m a x D V ( G , D ) ；此时 V(G,D∗) V ( G , D ∗ ) 衡量 Pdata,PG P d a t a , P G 之间JS divergency

maxD V(G,D)=maxD ∫x[Pdata(x)logD(x)+PG(x)log(1−D(x))]dx⇒D∗(x)=Pdata(x)Pdata(x)+PG(x) m a x D   V ( G , D ) = m a x D   ∫ x [ P d a t a ( x ) l o g D ( x ) + P G ( x ) l o g ( 1 − D ( x ) ) ] d x ⇒ D ∗ ( x ) = P d a t a ( x ) P d a t a ( x ) + P G ( x )

类比前面的LR的最优解 h∗θ(x) h θ ∗ ( x ) ， D∗ D ∗ 表示在先验概率相等的前提下，后验概率 P(x来自于真实data|x) P ( x 来 自 于 真 实 d a t a | x )

此时，

V(G,D∗)=∫x[Pdata(x)logPdata(x)Pdata(x)+PG(x)+PG(x)log(1−Pdata(x)Pdata(x)+PG(x))]dx=∫x[Pdata(x)logPdata(x)(Pdata(x)+PG(x))/2+PG(x)logPG(x)(Pdata(x)+PG(x))/2]dx−2log2=KL(Pdata(x)||Pdata(x)+PG(x)2)+KL(PG(x)||Pdata(x)+PG(x)2)−2log2=2JSD(Pdata,PG)−2log2 V ( G , D ∗ ) = ∫ x [ P d a t a ( x ) l o g P d a t a ( x ) P d a t a ( x ) + P G ( x ) + P G ( x ) l o g ( 1 − P d a t a ( x ) P d a t a ( x ) + P G ( x ) ) ] d x = ∫ x [ P d a t a ( x ) l o g P d a t a ( x ) ( P d a t a ( x ) + P G ( x ) ) / 2 + P G ( x ) l o g P G ( x ) ( P d a t a ( x ) + P G ( x ) ) / 2 ] d x − 2 l o g 2 = K L ( P d a t a ( x ) | | P d a t a ( x ) + P G ( x ) 2 ) + K L ( P G ( x ) | | P d a t a ( x ) + P G ( x ) 2 ) − 2 l o g 2 = 2 J S D ( P d a t a , P G ) − 2 l o g 2

1. 求解G使得 G∗=minGV(G,D∗) G ∗ = m i n G V ( G , D ∗ )

GAN的训练过程

（GAN的完整训练过程。图片来自于“李宏毅 深度学习”课程）
(Ian Goodfellow, 在原始论文中改训练G为 −log(D(G(z))) − l o g ( D ( G ( z ) ) ) , 这个训练目标是从收敛的角度来考虑的)

GAN的特别之处在哪里？

• ML的训练会可能很麻烦：采用显式的概率分布（模型空间可能不够准确）；采用隐式的概率推断会涉及比较复杂的方法
• GAN提供了另外一种方案，它直接利用BP来优化概率分布距离的方法：求解generator和discriminator的minimax博弈。generator和discriminator都采用neural network，有足够强大的表征能力（给一个表征能力的实验）。
• GAN提供了一个框架，可以将ML纳入进来，甚至可以按需设计其它的函数V（参见fGAN）

那么能否在GAN的框架下，将ML与原始GAN统一起来？能否使用其它的概率距离度量？

fGAN: GAN的统一框架

f-divergency

定义：

Df(P||Q)=∫xq(x)f(p(x)q(x))dx,且f是convex,f(1)=0 D f ( P | | Q ) = ∫ x q ( x ) f ( p ( x ) q ( x ) ) d x , 且 f 是 c o n v e x , f ( 1 ) = 0

例子：

• f=xlogx,Df(P||Q)=KL(P||Q) f = x l o g x , D f ( P | | Q ) = K L ( P | | Q )
• f=−logx,Df(P||Q)=revserse KL(P||Q) f = − l o g x , D f ( P | | Q ) = r e v s e r s e   K L ( P | | Q )

• f=ulogu−(u+1)log(u+1),Df(P||Q)=2JS(P||Q)−2log2 f = u l o g u − ( u + 1 ) l o g ( u + 1 ) , D f ( P | | Q ) = 2 J S ( P | | Q ) − 2 l o g 2

• f=ulogu-(u+1)log(u+1), D_f(P||Q) =2JS(P||Q) - 2log2$

Fenchel Conjugate:

f∗(t)=maxx∈Dom(f){xt−f(x)} f ∗ ( t ) = max x ∈ D o m ( f ) { x t − f ( x ) }

f(x)=maxt∈Dom(f∗){xt−f∗(t)} f ( x ) = max t ∈ D o m ( f ∗ ) { x t − f ∗ ( t ) }

（注： f∗(t) f ∗ ( t ) 也是convex, 它是一系列仿射函数的max）

事实上，Fenchel Conjugate定义了“斜率（梯度）到截距”的一种映射
当固定 t t , f∗(t)=maxx∈Dom(f){xt−f(x)} f ∗ ( t ) = max x ∈ D o m ( f ) { x t − f ( x ) } , 通过对x求导得到：

t=f′(x),f∗(t)=xf′(x)−f(x) t = f ′ ( x ) , f ∗ ( t ) = x f ′ ( x ) − f ( x )

上式可以看做参数方程的形式定义了 f∗ f ∗ ，它的几何意义：对任意的x，作f(x)的切线，斜率为t, 与y的截距的负数为 f∗(t) f ∗ ( t ) ; 它定义了斜率和负截距的映射关系。

重要的是，上述映射关系的对偶性质！

与GAN的联系

Df(P||Q)=∫xq(x)f(p(x)q(x))dx=∫xq(x)maxt∈dom(f∗){tp(x)q(x)−f∗(t)}dx≥maxt∈dom(f∗)∫xp(x)tdx−∫xq(x)f∗(t)dx D f ( P | | Q ) = ∫ x q ( x ) f ( p ( x ) q ( x ) ) d x = ∫ x q ( x ) max t ∈ d o m ( f ∗ ) { t p ( x ) q ( x ) − f ∗ ( t ) } d x ≥ max t ∈ d o m ( f ∗ ) ∫ x p ( x ) t d x − ∫ x q ( x ) f ∗ ( t ) d x

这里，令D(x) = t, 上式的下界可以写作：

maxD∫xp(x)D(x)dx−∫xq(x)f∗(D(x))dx=maxD{Ex∼p[D(x)]−Ex∼q[f∗(D(x))]} max D ∫ x p ( x ) D ( x ) d x − ∫ x q ( x ) f ∗ ( D ( x ) ) d x = max D { E x ∼ p [ D ( x ) ] − E x ∼ q [ f ∗ ( D ( x ) ) ] }

(事实上，如果D(x)表征能力足够强，最优解为 D∗(x)=f′(p(x)q(x)) D ∗ ( x ) = f ′ ( p ( x ) q ( x ) ) ,但是这个无法直接求解 )
对于GAN而言：

Df(Pdata||PG)≈maxD{Ex∼Pdata[D(x)]−Ex∼PG[f∗(D(x))]} D f ( P d a t a | | P G ) ≈ max D { E x ∼ P d a t a [ D ( x ) ] − E x ∼ P G [ f ∗ ( D ( x ) ) ] }

写成minimax形式：

G∗=argminGmaxDV(G,D) G ∗ = arg ⁡ min G max D V ( G , D )

按需挑选不同的f-divergency:

(不同的f-divergency对应的GAN, 图片来自于论文 f-GAN)

WGAN：解决收敛性问题

origin-GAN面临的收敛问题

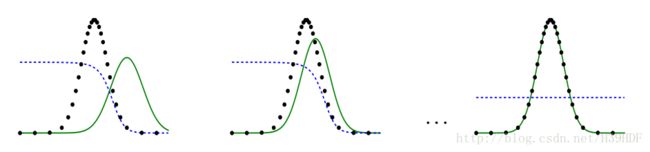
理想情况：D 指导 PG P G 往真实分布 Pdata P d a t a (dashed)运动

实际情况：D训练越好，完美区分，梯度消失，无指导能力

考虑”parallel lines distribution”, 二维分布 Pdata:(0,Z),其中Z∼U[0,1] P d a t a : ( 0 , Z ) , 其 中 Z ∼ U [ 0 , 1 ] , PG:(θ,Z) P G : ( θ , Z ) :

• JS(Pdata,PG)=|θ| J S ( P d a t a , P G ) = | θ |
• KL(Pdata||PG)=KL(PG||Pdata)=+∞(θ≠0),0(θ=0) K L ( P d a t a | | P G ) = K L ( P G | | P d a t a ) = + ∞ ( θ ≠ 0 ) , 0 ( θ = 0 )
• Discriminator D往往能将 Pdata,PG P d a t a , P G 完美分开
• 如上图所示，在D看来， d0,d50 d 0 , d 50 的JSD都是log2; D没有动力，让 PG P G 往“期望的方向”移动，会导致收敛问题
• 事实上，像生物进化一样，进化（比如眼睛）往往不是一蹴而就的；应该有更合适的度量方式，使得 PG P G 向 Pdata P d a t a “靠拢”（虽然此时JSD看来，generator并没有改善）

Earth Mover’s Distance

定义：对于概率分布P,Q，average distance of a plan γ γ :

B(γ)=∑xp,xqγ(xp,xq)||xp,xq|| B ( γ ) = ∑ x p , x q γ ( x p , x q ) | | x p , x q | |

Earth Mover’s Distance:

W(P,Q)=minγ∈ΠB(γ) W ( P , Q ) = min γ ∈ Π B ( γ )

示意图如下：
本质上， γ γ 就是一个联合概率，它的边缘分布分别为 P,Q P , Q

（ Moving Plan, 图片来自于“李宏毅 深度学习”）
在上面的 parallel line distribution例子里,

• W(Pdata,PG)=|θ| W ( P d a t a , P G ) = | θ |

WGAN

论文中证明，当我们采用Earth Mover’s Distance来度量 Pdata,PG P d a t a , P G 距离，相应的GAN形式如下(Kantorovich-Rubinstein duality, 来自论文“Optimal Transport: Old and New”)：

W(Pdata,PG)=maxD∈1−lipschitz{Ex∼Pdata[D(x)]−Ex∼PG[D(x)]} W ( P d a t a , P G ) = max D ∈ 1 − l i p s c h i t z { E x ∼ P d a t a [ D ( x ) ] − E x ∼ P G [ D ( x ) ] }

其中， 1-lipschitz 是指：

||D(x1)−D(x2)||≤||x1−x2|| | | D ( x 1 ) − D ( x 2 ) | | ≤ | | x 1 − x 2 | |

该条件的限制，防止了D(x)的变化过于剧烈。这里，整个优化目标有点“返璞归真”的意思了。
WGAN的论文中，使用weight-clipping近似1-lipschitz 条件：

• 权重 |w|>c⇒|w|=c | w | > c ⇒ | w | = c
• 实际使用的是k-lipschitz
  
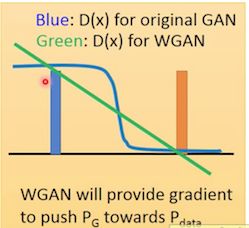
• 可以看到origin GAN 会存在梯度消失，无法有效指导 PG P G 的方向
• WGAN可以提供有效信息。
• W(Pdata,PG) W ( P d a t a , P G ) 的值可以作为训练好坏的参考

improved WGAN

将WGAN的1-lipschitz条件以惩罚项的形式引入：

​

W(Pdata,PG)=maxD{Ex∼Pdata[D(x)]−Ex∼PG[D(x)]}−λEx∼Ppenalty[(||∇xD(x)||−1)2] W ( P d a t a , P G ) = max D { E x ∼ P d a t a [ D ( x ) ] − E x ∼ P G [ D ( x ) ] } − λ E x ∼ P p e n a l t y [ ( | | ∇ x D ( x ) | | − 1 ) 2 ]

Ppenalty P p e n a l t y 的生成：对于 x∼Pdata,x̃ ∼PG x ∼ P d a t a , x ~ ∼ P G , 计算 x，x̃  x ， x ~ 之间的随机点，作为 x′∼Ppenalty x ′ ∼ P p e n a l t y

GAN的家族

Modify the optimization of GAN	Different structure from the original GAN
fGAN	Conditional GAN
WGAN	Semi-GAN
Least-square GAN	InfoGAN
Loss Sensitive GAN	BiGAN
Energy-based GAN	Cycle GAN
Boundary-Seeking GAN	IRGAN
Unroll GAN	VAE GAN
…	…