简单了解一下 Segment Tree 和 Fenwick Tree（Binary Indexed Tree）

转载请注明出处：http://blog.csdn.net/hjf_huangjinfu/article/details/77834729

先解决一个简单的问题

        考虑一下我们有一个简单问题，有一个数组 data [0 ~ n-1]，长度为n，给定后数组长度不会变化，现在有三个需求：

        1：我们需要查询该数组某一个范围内所有元素的和，比如 sum(i, j)，{0 <= i <= j <= n-1}。

        2：我们可以对数组任意位置的数据进行修改，修改后，任然需要继续满足需求1，也就是范围内的和。

        3：需求1和需求2的操作次数平均起来是相等的，比如100次操作中，有51次操作1，有49次操作2。

        问题链接：https://leetcode.com/problems/range-sum-query-mutable/description/

        方法1，一个常规方法：

        需求1：每次计算范围和，从i到j，对数组做遍历，然后累加，最后返回结果。

        需求2：直接对数组进行按索引修改。

        性能分析：

       时间复杂度：需求1，每次计算都要做一次遍历，那么平均复杂度为 O(n)。需求2，每次按索引对数组进行修改，平均时间复杂度为O(1)。需求3：由于需求1和需求2操作频率相当，所以需求3的平均时间复杂度为O(n)。

        空间复杂度：只需要一个存储sum的变量，平均空间复杂度为O(1)。

        咋一看这个方法还不错，O(n)的复杂度，也是实践可行的，但是会不会有可能有更好的方法呢？

        方法2，另外一个方法：

        计算机世界中，为了平衡性，运算时间和存储空间之间进行转换是常有的事情。对于上面这个问题，假如我们预先存储一些计算结果，会不会让计算的时间更快一点。

        需求1：使用一个新的数组，定义为 int[] s = new int[n];，该数组中每一个元素，存储的是原始数组中，从第0个元素到该元素的累加和，比如 s[i] = data[0] + .... + data[i]。这样的话，计算 sum(i, j)，只要做一次计算就可以，sum(i, j) = s[j] - s[i - 1];。

        需求2：修改元素data[i] 的话，需要对 s 数组的 [0 ~ i] 进行更新。

        示例图：

        性能分析：

       时间复杂度：需求1，构建数组s需要O(n)的时间，但是只需要构建一次，整体操作次数越多，影响越小，这里先忽略不计，   求和的时候，只需要做一次减法，所以平均复杂度为 O(1)。需求2，每次按索引对数组进行修改，都要修改数组s，所以平均时间复杂度为O(n)。需求3：由于需求1和需求2操作频率相当，所以需求3的平均时间复杂度为O(n)。

        空间复杂度：需要存储一个额外的数组s，所以平均空间复杂度为O(n)。

        咋一看这个方法还不如让方法1，让人很不开心。但是方法2却是让我们在前进的道路上迈出了跨越性的一步，就是 空间换时间。

        好吧，空间换时间是吧，方法2也是啊，怎么就不好用呢，仔细思考方法2，会发现方法2的一个特性，就是子问题是重叠的，也就是说 s[j] 内部是隐含包括 s[i] 的（i <= j）。在某种程度上，这是一个动态规划的思想。为什么子问题重叠不行呢，假如有索引（i <= j <= k）,如果我需要计算 sum(j, k) = s[k] - s[j - 1]; ,如果现在修改了data[i] ,对 sum(j, k) 的结果是毫无影响的，但是修改了data[i]后，需要对 s[k] 和 s[j] 的公共子问题 s[i] 进行修改，而这种修改是不必要的。

        既然问题分解成更小规模后，有重叠子问题这种情况，不适用于这个问题，那么考虑一下子问题不重叠的情况呢？这也就是分治思想。

        方法3，换个方法分解问题：

        把原始数组data，连续两个元素进行合并，合并的节点为这两个数据的父节点，父节点的数据为两个子节点的和，然后一直这样重复，直到最后合并为只有一个节点。

        示例图：

        需求1：如果需要计算 sum(i, j)，从整个树的根节点开始查找，根据查询边界（也就是i和j）和节点表示的范围进行比较，然后一直查询到树的叶子节点。比如我们要查询 sum(2， 6),如图所示，只需要计算这几个绿色节点的和就可以了。

        需求2：修改元素data[i] 的话，需要对该节点网上的所有父节点进行更新，比如更新data[5]，如下图所示，也就是红色节点。

        性能分析：

       时间复杂度：需求1，构建树需要O(log2n)的时间，但是只需要构建一次，整体操作次数越多，影响越小，这里先忽略不计，   求和的时候，从根节点一直搜索到叶子节点，所以平均复杂度为 O(log2n)。需求2，每次按索引对数组进行修改，都要修改整个树，但是只需要修改被修改节点的父节点，所以平均时间复杂度为O(log2n)。需求3：由于需求1和需求2操作频率相当，所以需求3的平均时间复杂度为O(log2n)。

        空间复杂度：需要存储一个额外的树，所以平均空间复杂度为O(n)。

        这下看起来有点效果了，花费了n的空间，换来了O(logn)的时间复杂度。

Segment Tree

        简介：Segment Tree，也叫区间树，是一种按区间来存储一个序列的某些信息的数据结构。很适合来解决上面提到的问题。详细信息参考连接：https://en.wikipedia.org/wiki/Segment_tree

        上面的方法3的思想，和区间树的思想是差不多的，都是构建成一颗完全二叉树。

        区间树可以存储任何区间信息，比如某个区间的最小值，或者某个区间的最大值，或者某个区间的和（上面提到的问题），等等。。

        构建一颗区间树：

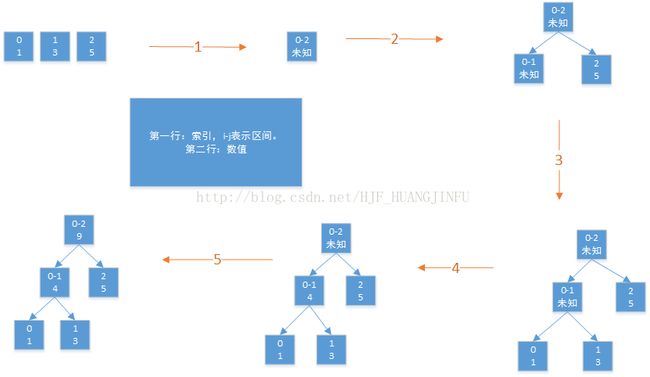
        自顶向下的递归法：

        1、把数组一分为二，生成一个节点，节点的信息为左半边数组和右半边数组信息的聚集。

        2、重复步骤1，直到所有叶子节点都是原始数组节点。

        示例图：

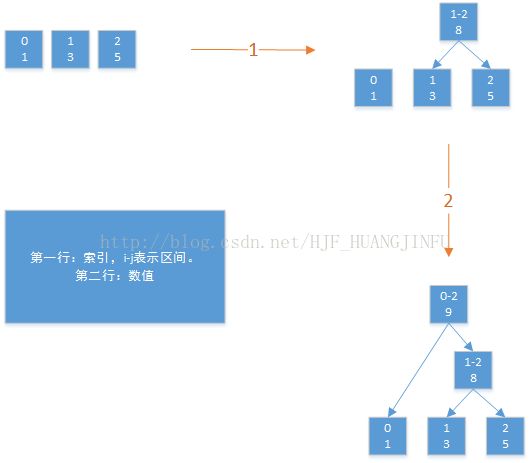
        自底向上的递推法：

        1、从后往前遍历数组，把节点两两聚合，生成父节点，碰到最后还有单个节点，就和上一层最右侧节点聚合，往更高一层聚合。

        2、重复步骤1，直到最后只有一个节点。

        示例图：

        由于递归法能直接反应该问题的性质，所以递归法比较容易理解问题。但是递归在实际使用中，性能堪忧，很容易造成方法栈溢出，所以在实际编码的时候，基本都使用自底向上的递推法。

使用 Segment Tree 解决上述问题的代码

        1、由于最后构造的树是一颗完全二叉树，所以整棵树节点数量是 2*n - 1。

        2、完全二叉树可以使用一个数组存储，因为如果一个节点位于索引i处，那么父节点为 i/2，左右子节点为 2*i，2*i + 1。

        3、注意，0索引位置不使用，因为有乘除法，所以如果索引为0的话，不能正确找到父子节点。

class NumArray {

    int[] st;
    int[] nums;

    public NumArray(int[] nums) {
        this.nums = nums;

        st = new int[nums.length * 2];
        construct(st, 1, nums, 0, nums.length - 1);
    }

    private void construct(int[] st, int stIndex, int[] data, int dataStartIndex, int dataEndIndex) {
        System.arraycopy(data, 0, st, st.length - data.length, data.length);
        for (int i = st.length - data.length - 1; i > 0; i--) {
            st[i] = st[i << 1] + st[(i << 1) + 1];
        }
    }

    public void update(int i, int val) {
        int index = st.length - nums.length + i;
        st[index] = val;

        index = index / 2;
        while (index >= 1) {
            st[index]  = st[index << 1] + st[(index << 1) + 1];
            index = index / 2;
        }
    }

    public int sumRange(int i, int j) {

        int sum = 0;

        i = i + nums.length;
        j = j + nums.length;

        //if i == j, loop finish, sum = st[i]
        while (i <= j) {

            //parent intersectcover
            if (i % 2 == 1) {
                sum += st[i];
                i++;
                continue;
            }
            if (j % 2 == 0) {
                sum += st[j];
                j--;
                continue;
            }

            //parent contain, up to parent
            i  = i >> 1;
            j  = j >> 1;

        }

        return sum;
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * obj.update(i,val);
 * int param_2 = obj.sumRange(i,j);
 */

使用 Segment Tree 存储隐藏信息

1、http://www.spoj.com/problems/BRCKTS/

        使用Segment Tree来存储什么信息？当一个区间中，'('  的数量和  ')' 的数量一样，并且成功匹配的数量也和他们相等时，就是正确的，每一次聚合，我们可以根据左右节点的左右括号数量和已匹配数量，来计算父节点的信息。使用区间树来存储左右括号数量和匹配数量。

2、https://leetcode.com/problems/count-of-smaller-numbers-after-self/description/

        使用Segment Tree来存储什么信息？先拷贝一份原始数组，然后对拷贝数组进行排序，然后从后往前遍历原始数组，每遍历一个值，找出它在排序后的索引，然后计算从0到当前索引的数据个数，然后把该索引数据个数加1。使用区间树来存储数据出现的次数。

Fenwick Tree（Binary Indexed Tree / BIT）

        BIT在功能上可以看成是一个特殊的区间树。也是存储某个区间的信息。

        参考链接：https://en.wikipedia.org/wiki/Fenwick_tree

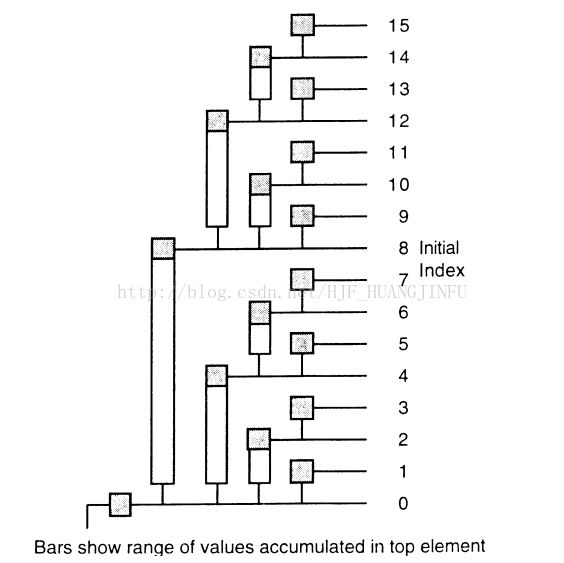
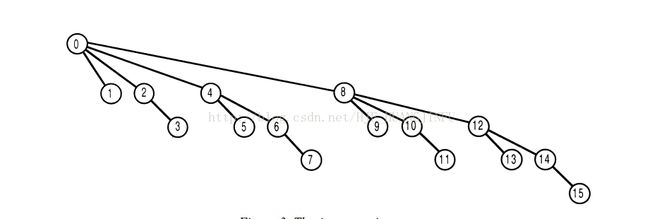
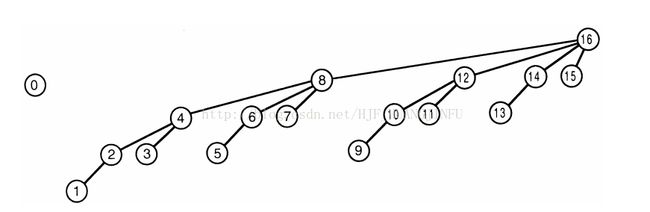
        示例图：

       

        区间树的区间是二分形成，而BIT的区间划分规则是这样的：

        假如索引为index = 10；又因为10的二进制表示为1010，只保留最右边的1，去掉左边其他所有的1后，变为0010，也就是2，所以，index的区间为[index - 2 + 1, index]。

        BIT的读取和写入操作都是自底向上的

        读操作，父节点索引为 index - index & (-index)。

        示例图：

      

        写操作，父节点索引为 index + index & (-index)。

        示例图：

         他与区间树的区别在于，BIT的代码更简洁，也更省空间。因为BIT不需要额外的存储原始数据信息。因为区间树的叶子节点是原始数据，所以需要的存储空间比BIT多。

        使用BIT解决上面的问题：

class NumArray1 {
    int bit[];
    int[] data;

    public NumArray1(int[] nums) {
        buildBIT(nums);
    }

    private void buildBIT(int[] nums) {
        this.data = new int[nums.length];

        bit = new int[nums.length + 1];
        for (int i = 0; i < nums.length; i++) {
            update(i, nums[i]);
            this.data[i] = nums[i];
        }
    }

    public int sumRange(int i, int j) {
        return sum(j) - sum(i - 1);
    }

    public void update(int i, int val) {

        int delta = val - data[i];
        i++;
        while (i <= data.length) {
            bit[i] += delta;
            i += i & (-i);
        }
    }

    private int sum(int endIndex) {
        endIndex++;
        int sum = 0;
        while (endIndex > 0) {
            sum += bit[endIndex];
            endIndex -= endIndex & (-endIndex);
        }
        return sum;
    }

}