排列的生成(三) —— 邻位互换法
1. 定义
是由Johnson-Trotter首先提出。如果已知n-1个元素的排列,将n插入到排列的不同位置,就得到了n个元素的排列。也可以直觉地认为,只要把排列中任意相邻的两个元素交换位置,就可以得到一个新的排列。
2. 算法
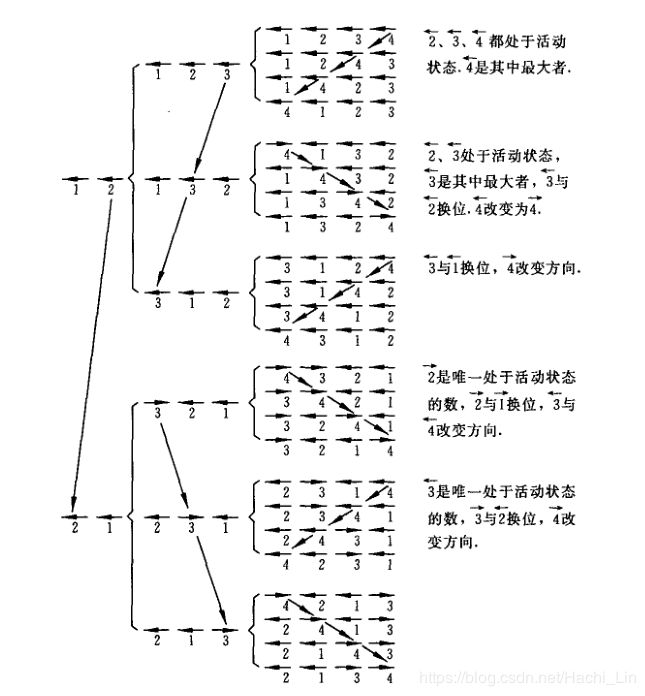
以 1 ← 2 ← 3 ← 4 ← 1^\gets2^\gets3^\gets 4^\gets 1←2←3←4←为初始排列,剪头所指一侧,相邻的数若比它小时,则称该数处在活动状态, 1 ← 2 ← 3 ← 4 ← 1^\gets2^\gets3^\gets 4^\gets 1←2←3←4←的2,3,4都处于活动状态。
p 1 p 2 … p n p_1p_2\dots p_n p1p2…pn生成下一个排列的步骤:
- S1: 若 p 1 p 2 … p n p_1p_2\dots p_n p1p2…pn没有数处于活动状态则结束。
- S2: 将处于活动状态的各数中值最大者设为 m m m,则 m m m和它的剪头所指一侧相邻的数互换位置,而且比 m m m大的所有数的剪头改变方向,即 → \to →改为 ← \gets ←, ← \gets ←改为 → \to →,转S1。
2.1 求排列1234的下一个排列
2.2 求排列12345生成的第100个排列数是多少
通过2.1可以看出每个数字经过多少次排列向左或向右(初始移动是向左)移动一位,如下表
| 数字 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 次数 | 60(3 ×4×5) | 20(4×5) | 5(1×5) | 1 |
所以这100次排列当中,
- 5排列了100次
- 4排列了20次
- 3排列了5次
- 2排列了2次。
因为总共有5位数,所以5每经过10次排列后会回到起点,4每经过8次排列后会回到起点,3经过6次排列后会回到起点,2不会回到起点,2最多只能排列2次。因此
(1)100/10=10,余数为0,说明此时5在第5位。(考虑全部数字)—— _ _ _ _ 5
(2)20/8=2,余数为4,说明此时4在第1位。(不考虑数字5)—— 4 _ _ _ 5
(3)5/6=0,余数为5,说明此时3在第2位。(不考虑数字4,5)—— 4 _ 3 _ 5
(4)2排列了2次,此时的对应的两位数是21。(不考虑数字3,4,5)—— 4 2 3 1 5
因此排列12345生成的第100个排列数是42315。
2.3 求 23541是排列12345生成的第几个排列
12345生成的排列总共有 5 ! = 120 5!=120 5!=120个。
通过2.2分析知道
(1)不考虑345,序列21表明了2排列了2次(移动了1次)
(2)不考虑45,序列231表明3排列了5次(移动了4次)
(3)不考虑5,序列2341表明4排列了18次(移动了17次)
此时,根据2.2的表就可以猜了,5排列了至少 max { 1 × 60 + 1 , 4 × 20 + 1 , 17 × 5 + 1 } = max { 61 , 81 , 86 } = 86 \max \{1\times 60+1,4\times20+1,17\times 5+1\}=\max\{61,81,86\}=86 max{1×60+1,4×20+1,17×5+1}=max{61,81,86}=86次刚好满足上述要求,最后一个要求是要满足5的位置,5处于第3位,86/10=6余数是1,说明这是5还在第1位,增加1次排列即可让5在第3位而又可以满足(1)(2)(3)条件,此时可知88即为最终所求。