程序员的数学---数学思维的锻炼

第三章： 余数–周期性和分组

星期问题

来看一道简单的题目：今天星期日，那么 100 天以后星期几？
这个问题最笨的方法就是数数了。不过那样也是颇为费事，从余数方向考虑：一个礼拜 7 天，100 天等于 14 个礼拜周期还剩两天（100 = 14*7 + 2）。于是答案就是星期 2 了。

假设现在题目变成了 1 亿天之后是星期几，我们还是可以用取余的思想：100000000 = 14285714*7 + 2 。同样的， 答案也是星期 2 。

如果数字再大一点，10^210 天之后是星期几呢？这么大的数字，如果用计算器直接计算肯定是不行的，一般的编程语言也没有存这么大数据的整形数据类型。我们这一次还是利用余数的思想：

10^0 = 1 除以 7 结果为 0 余 1
10^1 = 10 除以 7 结果为 1 余 3
10^2 = 100 除以 7 结果为 14 余 2
10^3 = 1000 除以 7 结果为 142 余 6
10^4 = 10000 除以 7 结果为 1428 余 4
10^5 = 100000 除以 7 结果为 14285 余 5 

10^6 = 1 除以 7 结果为 142857 余 1
10^7 = 10 除以 7 结果为 1428571 余 3
10^8 = 100 除以 7 结果为 14285714 余 2
10^9 = 1000 除以 7 结果为 142857142 余 6
10^10 = 10000 除以 7 结果为 1428571428 余 4
10^11 = 100000 除以 7 结果为 14285714285 余 5 

10^12 = 1 除以 7 结果为 142857142857 余 1

我们已经可以看出规律了，余数以 1、3、2、6、4、5 的顺序循环，也就是说，1 后面每增加 6 个 0，余数也即星期数和增加前相同。那么 10^210 天后的星期数为 210（1 后面一共 210 个 0） % 6 的值对应上述循环的结果（1（下标为 0）、3（下标为 1）、2（下标为 2）、6（下标为 3）、5（下标为 4）、4（下标为 5）），即为星期 1。

乘方的思考题

1234567^(987654321) 的个位数是什么？ 手算？计算器？事实上这两种方法都行不通，原因就是因为数字太大了。**事实上，一个数的 n 次方的末位数只和这个数本身的末位数和 n 有关。** 我们来看一下：

1234567^0 的个位数 = 1
1234567^1 的个位数 = 7
1234567^2 的个位数 = 9
1234567^3 的个位数 = 3

1234567^4 的个位数 = 1
1234567^5 的个位数 = 7
1234567^6 的个位数 = 9
1234567^7 的个位数 = 3

1234567^8 的个位数 = 1
1234567^9 的个位数 = 7

我们发现规律了：个位数是1、7、9、3 这四个数的循环。所以 1234567^(987654321) 的个位数其实就等于 987654321 % 4 的结果对应1、7、9、3 这四个数就可以了：因为 987654321 % 4 = 1，所以答案是 7。
即 1234567^(987654321) 的个位数为 7 。

哥德堡的七桥问题

这个问题源于一个故事：很久以前，一个叫哥尼斯堡的小城，小城被河流分成了 4 块陆地（图中编号为 A、B、C、D）。人们为了连接这些陆地，建立了 7 座桥：

现在问题是需要寻找出走遍 7 座桥的方法，但是需要遵守以下条件：

1、走过的桥不能再走
2、可以多次经过同一块陆地
3、可以以任意陆地为起点和终点

其实这个就是 “一笔画” 的问题，如果每一种情况都去试一下的话，是相当复杂和有难度的。我们来考虑简化一下问题模型：将陆地简化成图的顶点，把桥简化成图的边，那么这个问题就可以创建出以下的模型：

我们仔细思考一下，假设对于这个图我们可以找出符合规则的走法，那么每当经过一块陆地时（一个图顶点），如果这个顶点不是起点或者终点，该顶点的度（边）应该减 2 （走到这块陆地需要消耗一座桥，走出这块陆地需要消耗一座桥）。那么扩展到全图的顶点来说，除了起点和终点，其他所有顶点的度应该是 2 的倍数（即为偶数），因为每经过一个块陆地都需要消耗和这块陆地相连的 2 座桥。
而对于起点和终点来说呢？因为没有限制起点和终点是否可以相同，那么需要分两种情况：

1、起点和终点为同一个点：这种情况下，我们从一个点开始最后还要回到这个点，
	所以这个起点的度也需要是 2 的倍数（偶数），此时图中所有的顶底的度应该为偶数；

2、起点和终点不是同一个点：这种情况和上面情况相反，需要满足起点和终点的度为奇数，
	所以此时图中应该有两个顶点的度为奇数，其他顶点的度为偶数。

好了，我们已经知道了规律了，如果一个图可以按照上述定义的条件走完，那么其中顶点应该满足以下两个条件之一：

1、图中所有的顶点的度为偶数
2、图中两个顶点的度为奇数（对应起点和终点），其他顶点的度为偶数

我们回头再看一下上面我们建立的图模型：其中所有顶点的度都为奇数，因此对于上述图我们无法找出符合上述规定条件的走法。

课后对话

学生：老师，我的人生出现了 360 度的大转弯呢！ 老师：360 度的话，不就没发生变化吗？

第四章： 数学归纳法

数学归纳法是证明有关于整数的结论对于 0 以上的所有整数（0、1、2、3、4…）是否成立时所用的方法。

假设现在要用数学归纳法证明：结论 P(n) 对于 0 以上的所有整数 n 都成立。我们需要经过两个步骤：

步骤1：
	证明 P(0) 成立；
	
步骤2：
	证明不论 k 为 0 以上的哪个整数，若 “P(k) 成立，则 P(k+1) 也成立”。

步骤 1 中，要证明 k 为 0 时结论 P(0) 成立，我们称其为 基底。
步骤 2 中，要证明无论 k 为 0 以上哪个整数，" 若 P(k) 成立，则 P(k+1) 成立"。我们把步骤 2 称作 归纳。
如果步骤 1 和步骤 2 都能得到证明，就证明了 结论 P(n) 对于 0 以上的所有整数 n 都成立。

高斯的结论

在你面前有一个空的存钱罐。
第一天往存钱罐里投入 1 元。
第二天往存钱罐里投入 2 元。
第三天往存钱罐里投入 3 元。
第四天往存钱罐里投入 4 元。
第五天往存钱罐里投入 5 元。
那么第 100 天投入前之后总金额为多少？
这个问题其实就是求 （1 + 2 + 3 + 4 + … + 100）的值。如果我们没有学过等差数列等一些数学知识，最容易想到的方法就是逐个想加了。数学王子高斯 9 岁时候也遇到了这个问题，高斯用了一个很巧妙的方法，很快就得出了答案。
高斯是怎么算的呢：
1 + 2 + 3 + 4 + … + 100 顺序计算的结果和 100 + 99 + 98 + … + 1 的逆向计算结果应该是相同的，那么，就将这两串数字像下面那样纵向想加：
1 + 2 + 3 + 4 + … + 100
100 + 99 + 98 + 97 + … + 1
一共是 100 个 101，即为 10100，但是这个是答案的 2 倍, 所以还得除以 2 ，即答案为 5050。

后来，高斯得出了一个结论：0 到 n 的整数和为 (n*(n + 1)) / 2 。
这个结论肯定是正确的，下面我们用数学归纳法证明一下：

1、证明基底 P(0) 成立：
	此时 P(0) 就是：0 ~ 0 的整数和是 (0*(0 + 1))/2, 结果为 0 。步骤 1 成立、
	
2、归纳的证明：
	证明当 k 为 0 以上的任意整数时，“若 P(k) 成立，则 P(k+1) 也成立”
	先假设 P(k) 成立，即 0 ~ k 的整数和为 (k*(k + 1))/2，这时一下等式成立：
	0 + 1 + 2 + 3 + .... + k = (k*(k + 1))/2。
	要证明：
	0 + 1 + 2 + 3 + .... + k+1 = ((k+1)*((k+1) + 1))/2
	等式的左边等于：
	(k*(k + 1))/2 + k+1 = (k*(k + 1))/2 + 2*(k+1)/2 = ((k+2)*(k+1))/2
	等式的右边等于： ((k+1)*((k+1) + 1))/2 = (k+2)*(k+1)/2
	等式的左边和右边推导的结果相同，结论得证

我们再用数学归纳法来证明一个结论：

求出奇数的和

结论 `P(n)：1 + 3 + 5 + 7 + 9 + .... + (2 * n - 1) = n^2` 我们来举几个简单的例子：

P(1)：1 = 1^2
P(2)：1 + 3 = 2^2
P(3)：1 + 3 + 5 = 3^2
P(4)：1 + 3 + 5 + 7 = 4^2

以上的举例确实是成立的。下面用数学归纳法来证明这个结论：

步骤 1 ，证明 P(1) 成立，因为结论的开始数是 1 ，所以我们的基底即为 P(1) ：
	因为 P(1) = 1 = 1^2 ，所以基底得证；

步骤 2 ，归纳的证明，证明 k 为 1 以上的任意整数时，“若 P(k) 成立，那么 P(k+1) 也成立”。
	先假设 P(k) 成立，即以下等式成立：
	1 + 3 + 5 + ... + (2*k-1) = k^2
	要证明的等式：
	1 + 3 + 5 + ... + (2*k-1) + (2*(k+1)-1) = (k+1)^2
	等式左边等于：
	k^2 + (2*(k+1)-1) = k^2 + 2*k + 1 = (k+1)^2 // 因式分解
	此时，等式左边等于等式右边，步骤 2 得证，即结论得证。

课后对话

老师：首先假设一条腿可以往前迈一步。 学生：嗯。 老师：然后假设另一条腿无论什么情况都能迈出去 学生：那么会怎么样？ 老师：那样的话，就能够行进到无限的远方，这就是数学归纳法。

第五章： 排列组合

32 个灯泡

1 个灯泡有亮和灭 2 种状态，如果 32 个这样的灯泡排成一排，则有多少种亮灭模式？ 很简单的思考题，往细想，1 个灯泡有 2 种亮灭模式，2 个灯泡就有 2*2 种亮灭模式，3 个灯泡就有 2*2*2 种亮灭模式...... 32 个灯泡就有 2^32 种亮灭模式。这个数值其实就是 C语言 中 4 字节的无符号整形（unsigned int）的数值最大值。 **n 位二进制数可以表示的数的总数为 2^n 。**

置换

3 张牌的置换：如果将 A、B、C 这 3 张牌按 照 ABC、ACB、BAC ...... 等顺序排列，那么共有多少种排法？ 答案很简单，就是 6 种：ABC、ACB、BAC、BCA、CAB、CBA。 如本题那般，**将 n 个事物按照顺序进行排列成为置换。** A、B、C 3 张牌的置换总数，可以通过下面的步骤得出： 第一个位置可以有 A、B、C 3 种选择； 第二个位置有 2 种选择，因为第一个位置已经选了一张牌； 第三个位置只有 1 种选择，因为前两个位置已经选了 2 张牌。 那么置换的种数：3*2*1 = 6。 归纳一下：**n 张牌的置换种数有 `n!` 种，即为 n * (n-1) * (n-2) *......* 1**

排列

从 5 张牌（A、B、C、D、E）中选出 3 张牌进行排列，一共有多少种排法？ 答案：60 种， 第一个位置的取法有 5 中； 第二个位置的取法有 4 种（有一张牌被第一个位置选了）； 第三个位置的取法有 3 种（两张牌被前面两个位置选了）。 即结果为：5 * 4 * 3 = 60。 归纳一下：**从 n 张牌中取出 k 张的进行排列的总数为：n * (n-1) * (n-2) * (n-3) * ...... * (n-k+1) 种。** 我们在高中的时候将排列用 A 表示，即 A _n^k = n * (n-1) * (n-2) * (n-3) * ...... * (n-k+1)

组合

从 5 张牌（A、B、C、D、E）中选出 3 张牌，不考虑它们的顺序，一共有多少取法？ 这种取法成为**组合**。“置换” 和 “排列” 是考虑顺序的，而 “组合” 不考虑顺序。对于组合，我们这样考虑就可以了： 首先，和排列一样 “考虑顺序” 进行计数。但是这样并不正确，因为排列会出现 ABC、ACB、BAC、BCA、CAB、CBA 这 6 种排法，但其实作为组合这 6 种情况都看作一种情况。那么 接下来，将结果除以重复计数部分（置换数）。 所以结果为 A ₅ ³ / P _k ^k = 60 / 6 = 10。（P 为置换）。 我们将组合用 C 表示，即： C _n^k = A _n^k / P _k^k （P 为置换） = n! / (n-k)! / k! = n! / ((n-k)!*k!) = n(n-1)(n-2)......(n-k+1) / (1*2*3*......*k)

置换、排列、组合 3 者的关系：
C _n^k = A _n^k / P _k^k

药品调剂

现在假设要将颗粒状药品调剂成一种新药。药品有 A、B、C 三种，新药品调剂规则如下：

从 A、B、C 这 3 种药品中，共取出 100 粒进行调剂
调剂时，A、B、C 这 3 种每种至少有 1 粒
不考虑药品的顺序
同种药剂每粒都相同

新药品调剂组合共有多少种？

缩小问题规模思考

如果直接考虑 100 粒药品的话数字较大，我们把数字缩小点：把 100 粒改成 5 粒。我们准备好 5 个盘子放入药品，再在 5 个盘子之间加入两个隔板，如图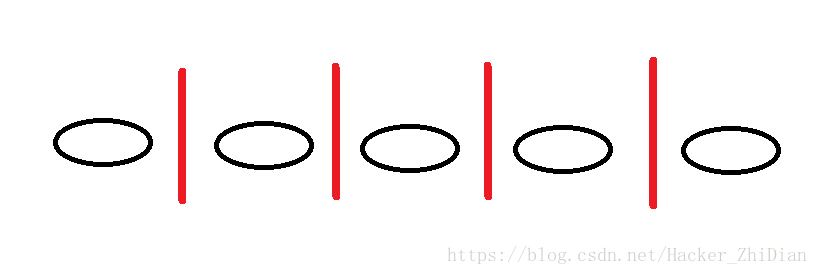：  红色线条部分代表我们可以放入隔板的位置。于是一共有 4 个隔板位置，我们需要把 2 个隔板放入这 4 个位置，并且规定：第一个隔板前放入药品 A，第一个隔板和第二个隔板之间放入药品 B，第二个隔板后面放入药品 C。那么一种可能的情况如下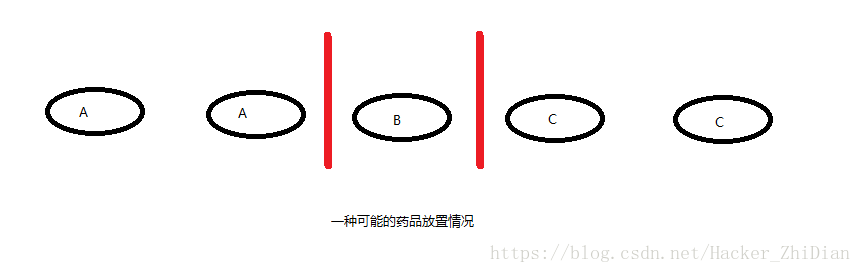：  那么总的情况数有多少种呢？很明显是 4 个位置中选两个位置插入隔板的可能情况数。即 C ₄² = 6 我们可以总结出规律了：`从 k 种药品中选出 n 粒，所有的可能情况数为：` C _n-1^k-1 。所以从 3 种药品选出 100 粒的组合方法数为 C ₉₉² = 99*98 / (1*2) = 4851

利用逻辑思考

这道题还可以用另一种方法解决：利用逻辑：

根据要求，我们假设先取 A 药剂 98 粒，那么 B 药剂和 C 药剂就只能各取 1 粒，这里面包含 1 种取法；
接下来我们假设先取 A 药剂 97 粒，那么此时 B 药剂可以取 2 粒也可以取 1 粒，这里面就包含了 2 种取法；
继续，假设先取 A 药剂 96 粒，此时 B 药剂可以取 1 、2、3 粒，这里面包含了 3 种取法 ；

......

最后取 A 药剂 1粒，此时 B 药剂可以取 1、2、3、4、......、98 粒，这里面包含了 98 种取法；
那么最后总的的取法总数为：1 + 2 + 3 + 4 + ...... + 98，
根据第四章中高斯的结论结果即为 98*(1+98) / 2 = 4851

再来看一道题目：

至少一端是王牌

现在有 5 张扑克牌，其中 2 张是王牌（大小王），J、Q、K 各一张。将这 5 张牌排成一排，左端或者右端至少有一端王牌的排法有多少种？

正向思考

先来看一下正向思考的思路： 左端是王牌的情况：

假设将王牌至于左端，那么左端的选法就有大王或者小王两种选法，剩下 4 张的排法即为 4 张牌的置换数，
此时总的排法为：2 * 4！ = 48

右端是王牌的情况：

和左端是王牌一样，也是有 48 种排法

最后还需要去掉两端都是王牌的重复数，左端是王牌的情况中包含了两端都是王牌的情况，同理，右端是王牌的情况中也包含了两端都是王牌的情况，因此需要去除重复，此时的重复为两段都是王牌的情况（2）乘以剩下三张牌的置换（3!）即：

左端是王牌 + 右端是王牌 - 两端都是王牌 = 48 + 48 - 2*3! = 84

利用逻辑反向思考

其实这道题还可以利用逻辑来反向思考，我们知道：
左端和右端至少有一张是王牌的排列数 = 所有牌的置换数 - 左端和右端都不是王牌的排列数，现在问题就是求出左右端都不是王牌的排列数：我们可以从 J、Q、K 三张牌中选出两张牌作为左右两端的牌进行排列，即 A ₃² = 6，接下来就是剩余的 3 张牌自由排列：A ₃³ = 6，所以左右端都不是王牌的排列数为 6*6 = 36。

那么最后的结果即为：A ₅⁵ - A ₃² * A ₃³ = 120 - 36 = 84

课后对话

学生：我觉得有 n、k 等变量的地方很难掌握 ....... 老师：那就先从 5 或者 3 等较小的数开始练习！ 学生：可是遇到大数时就会担心结果是否正确...... 老师：所以需要使用 n、k 将问题抽象化嘛！

第六章 ：递归

汉诺塔问题

相信大家已经听说过这个问题，这里还是给出其的具体描述：

有三根柱子，这里编号为 A 、 B 、 C，一开始在A柱子上有从下往上按照从大到小顺序摆放的64个圆盘，给的任务是将这些圆盘以同样的大小顺序摆放到C柱子上，可以借助任何柱子作为中转，但是限制条件是：

1.在小圆盘上不能放大圆盘。 
2.在三根柱子之间一次只能移动一个圆盘。 
3.只能移动在最顶端的圆盘。

那么要把 64 个圆盘从按上述规则从 A 柱子移动到 C 柱子，一共需要移动多少次呢？
64 个圆盘对我我们思考来说极为不利，不妨试试将圆盘的个数缩小点，我们来看看 3 个圆盘的情况：

我们来一个一个移动：

至此，我们把 A 柱子上的上面 2 个小的圆盘借住 C 柱子移动到了 B 柱子上，接下来我们要把 A 柱子上最大的圆盘移动到 C 柱子上：

接下来，我们要把 B 柱子上的 2 个圆盘借住 A 柱子移动到 C 柱子上：

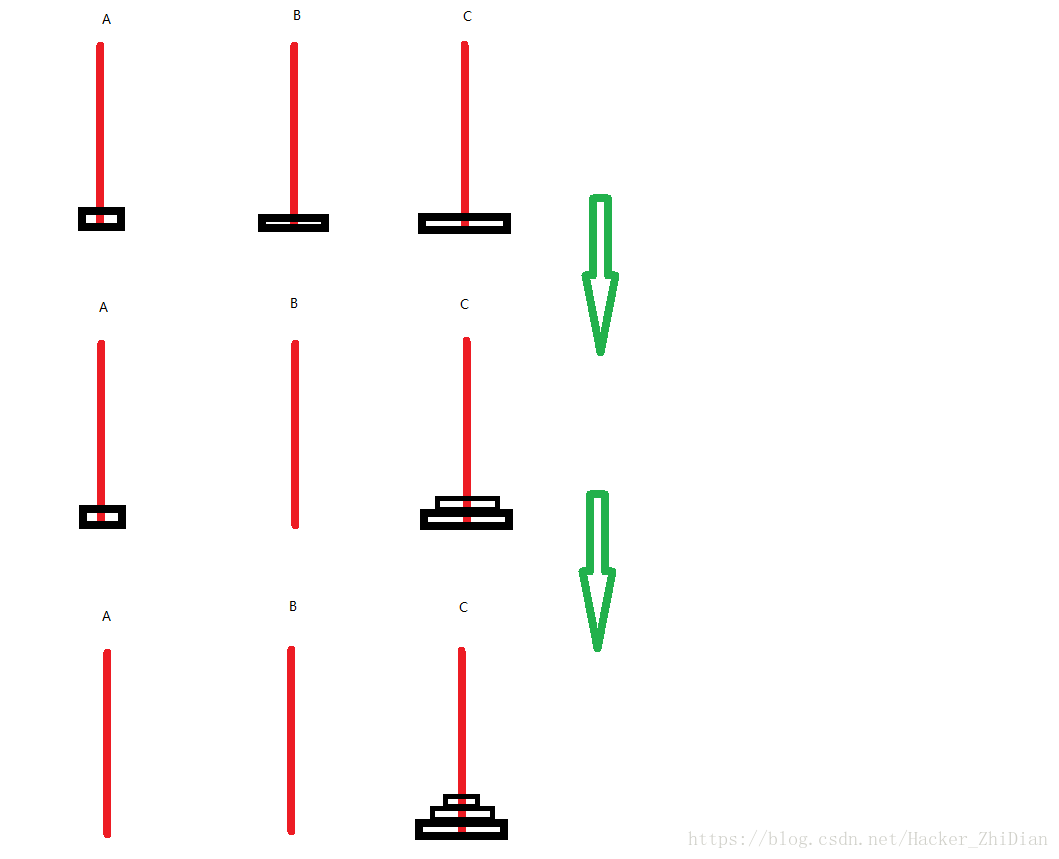
Ok， 移动完成，可以看到一共用了 7 步，通过对 3 个汉诺塔问题的图解，我们可以归纳出汉诺塔问题的结论了：
对于 n 个圆盘的汉诺塔问题，要把 A 柱子上所有的圆盘按以上规则移动到 C 盘：
1、先把 A 柱子上小的的 n-1 个圆盘通过 C 柱子作为中转移动到 B 柱子上；
2、把 A 柱子上最底下的那个圆盘移动到 C 柱子上；
3、再通过 A 柱子作为中转将 B 柱子上的 n-1 个圆盘移动到 C 盘上。

我们可以用公式表示出移动的过程：

这个公式正好对应上面的三个步骤：

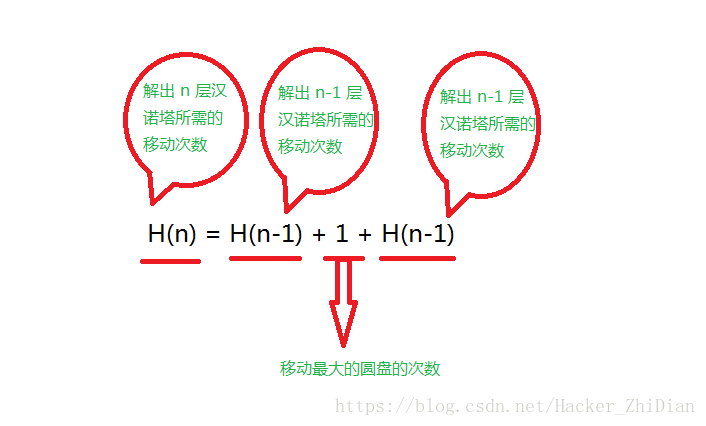
那么我们根据这个公式也可以推出 n 个汉诺塔所需要的移动次数了：H(n) = 2ⁿ - 1
于是移动 64 个汉诺塔所需要的次数为 2^64 - 1 。我们可以用程序写出这个步骤：

#include 

int moveTimes = 0; // 移动次数
 
// 将 n 个圆盘从 A 柱子移动到 C 柱子 
void hanoi(int n, char A, char B, char C) {
	if (n == 0) {
		return ;
	}
	// 将 n-1 个圆盘从 A 柱子借住 C 柱子移动到 B 柱子 
	hanoi(n-1, A, C, B);
	// 移动 A 柱子上最下面的那个圆盘到 C 柱子 
	printf("第 %d 次移动：%c --> %c\n", ++moveTimes, A, C);
	// 将 n-1 个圆盘从 B 柱子借住 A 柱子移动到 C 柱子 
	hanoi(n-1, B, A, C);
}

int main() {
	int n;
	scanf("%d", &n);
	hanoi(n, 'A', 'B', 'C');
	
	return 0;
} 

来看看运行结果：

其实以前就写过一篇关于汉诺塔的文章，只不过当时并没有讲的这么细致，附有 C++ 语言的实现代码，丝路上略有一点点不同，有兴趣的小伙伴可以看看 汉诺塔和 N 皇后问题

斐波那契数列

斐波那契我想你应该耳熟能详了，因为它实在是在太常见了，因其衍生出来的问题也有很多，斐波那契数列是一个递推式，其公式为：  我们也很容易能根据这个递推公式写一个最基础的求斐波那契数列第 n 项 F(n) 的值的程序：

#include 

int f(int n) {
	if (n == 1 || n == 2) {
		return 1;
	}
	return f(n-1) + f(n-2);
}

int main() {
	int n;
	scanf("%d", &n);
	if (n > 0) {
		printf("%d", f(n));
	}
	return 0;
}

但其实这个算法的时间复杂度是相当高的（2 ⁿ 级别），这种级别的时间复杂度， n 等于 40 的时候就够呛了。我们很容易通过循环的方式来改进这个算法：

#include 

int f(int n) {
	int res = 0, a = 1, b = 1;
	int i = 3;
	for (; i <= n; i++) {
		res = a + b;
		b = a;
		a = res;
	}
	return res;
}

int main() {
	int n;
	scanf("%d", &n);
	if (n > 0) {
		printf("%d\n", f(n));
	}
	return 0;
}

这样的话时间复杂度为 O(n)，比上面那个快了不少，其实求斐波那契数列的还可以在 O(logn) 的时间复杂度内完成，利用矩阵快速幂就可以做到，这里就不细讲了，有兴趣的小伙伴可以看一下这篇文章：快速幂和矩阵快速幂。

由斐波那契数列衍生出来的问题有很多，比较著名的有一次走 1 阶或者 2 阶，走 n 阶台阶，共有多少种走法、葵花种子的排法、植物枝叶的长法等。

帕斯卡三角形

其实这个就是我们所熟知的杨辉三角，看张图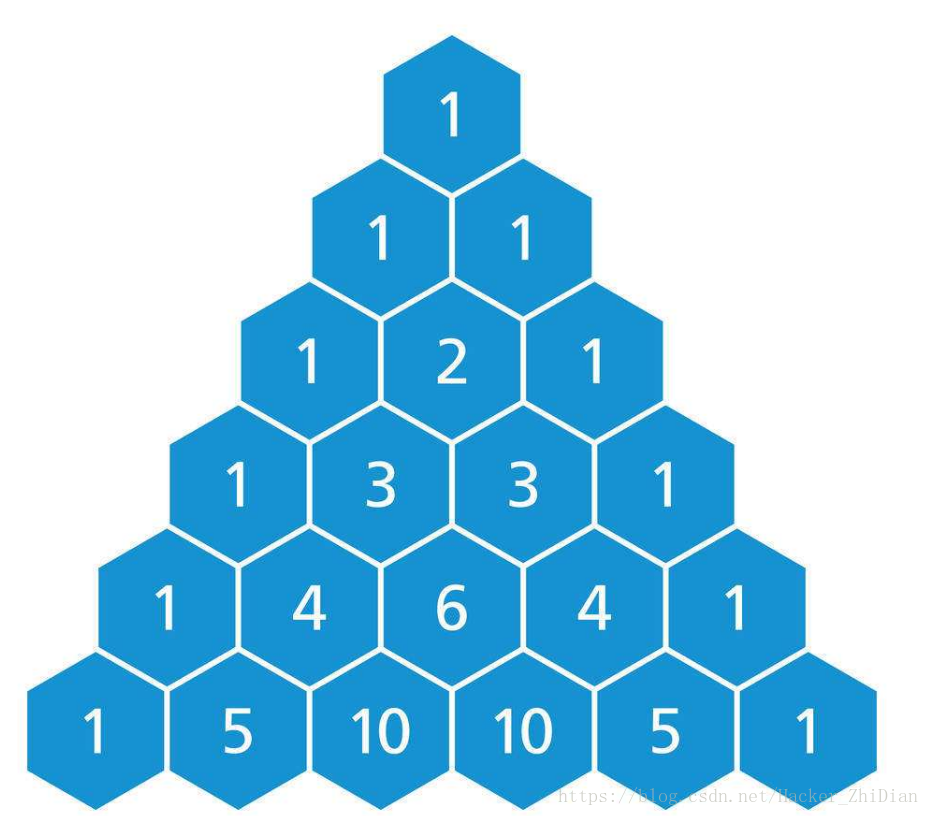：  百度上的一张图，我们知道杨辉三角有一个特点：如果当前位置的列数为 1 或者当前行编号和列编号相等，则这个位置的值为 1，否则为位于其上面两个数的和。其实，杨辉三角的元素值还有下面的特点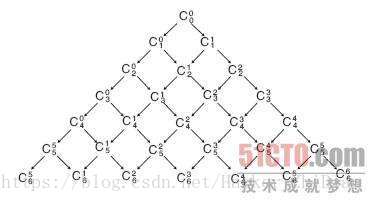：  百度上的图，我们可以看到，杨辉三角每个位置上的值还和组合数（参考上文组合部分）有关。那么结合上面讲的结论，就可以推出下面的结论：

C ₂¹ = C ₁⁰ + C ₁¹

C ₃¹ = C ₂⁰ + C ₂¹

C ₃² = C ₂¹ + C ₂²

…

C _mⁿ = C _m-1^n-1 + C _m-1ⁿ

那么这个结论代表什么意思呢？我们把 n 设成 5 ，m 设成 3 来看看：

5 中选 3 的组合数 等于 4 中选 2 的组合数 加上 4 中选 3 的组合数，如果还没理解，那么再具体一点：
从 A、B、C、D、E 5 张牌中选择 3 张牌的组合数为包含 A 的组合数 加上 不包含 A 的组合数。
如果选 A，那么结果为 C ₄² ，否则就是不选 A，结果为： C ₄³ ，于是 C ₅³ = C ₄² + C ₄³

原来如此，通过对是否包含 A 进行讨论，兼顾了完整性和排他性并且没有重复。而这从某个应用角度上来说也代表了上面推理出来的公式的意义。
最后总结一下解决递归问题的要领：

1、从整个问题中隐去部分问题，即相当于当前先处理一个特殊的情况
2、把剩下的问题变成同类问题通过缩小参数给 “下属” 去解决

对于一个递归问题，如果能够写出其递推式，那么这个问题已经解决了 2/3，剩下的就是考虑编程时的时间复杂度和空间复杂度了。

课后对话

学生：把握结构是关键吧？ 老师：对！非常关键！ 学生：为什么呢？ 老师：因为把握结构是 “分解” 整个问题的突破口。

第七章： 指数爆炸

折纸问题

假设现在有一张厚度为 1mm 的纸，纸质非常柔软，可以对折无数次，每次对折，厚度便翻一番。 已知地球距月球距离 39 万公里，请问对折多少次之后可以超过地月距离？

表面看上去这道题有点异想天开，从直觉上说，就算是对折成千上万次也未必能达到目的。事实真的如此吗，我们不妨试试：

1 --> 2mm
2 --> 4mm
3 --> 8mm
4 --> 16mm
5 --> 32mm
6 --> 64mm
7 --> 128mm
8 --> 256mm
9 --> 512mm
10 --> 1024mm

我们发现：纸的厚度 = 2^对折次数 mm，我们把问题转换一下：
39万公里 = 390000km = 390000000m = 390000000000mm
其实就是问 2 的多少次方会大于等于 390000000000 。也就是说答案是 log ₂^390000000000 mm 的整数值向上取整（对折次数不能是小数）。理解了这个，我们就用程序来做这道题吧：

#include  
#include 

int main() {
	// 调用了 math.h 头文件中的 log2 函数，用于求出数学上 log2(n) 的值
	double res = log2(390000000000);
	if (res > (int)res) {
		res++;
	}
	printf("%d", (int)res);
	return 0;
}

结果：

只需要39次！？对的，其实就只需要 39 次，这就是指数爆炸的威力。我们来看一张指数函数的函数图像：

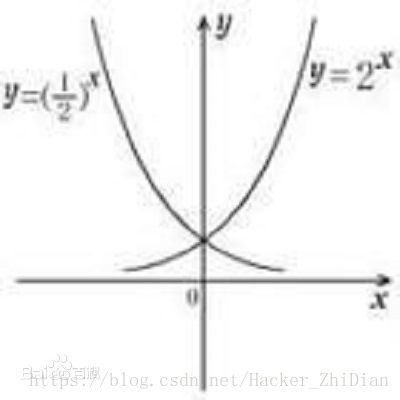
这幅图是从百度上找的，事实上，x 越大，曲线就会越垂直，也就是曲线在某个点的斜率会越大，即函数值增长的速度越快。到了后面，函数图像几乎是平行于 y 轴！

在我们设计算法的时候，如果一个算法的时间复杂度达到了指数级，那么这个算法的效率是非常低的，应该要找办法优化。

二分查找

二分查找是一个根据指数爆炸发明的查找算法，其可以在 log(n) 的时间复杂度内找到一个有序序列中某个特定的值（请注意是有序序列）。

假设我们现在要在数组 4、4、2、1、3 中查找数字 2：
1、先对数组进行从小到大排序：1 2 3 4 4

2、比较 2 和数组中间的数字 3 的大小，明显，2 小于 3，于是在数组的左半边继续二分查找。

3、在 1 2 这两个数字中查找数字 2 ，此时我们取得中间的那个数应该是 1 ，小于 2，于是在 1 的右边 3 的左边查找。
4、在 1 的右边和 3 的左边就只有 2 了，那么数字 2 就被找到了，如果还没找到，证明这个数组没有要查找的数字。

在这里为什么我们要对数组进行排序呢？其实是为了确定一个参照 “规则”，怎么理解呢？
我们必须确保对于当前每一个查找到的数，我们都可以通过这个数来判断要查找的目标数在这个数的左边或者在这个数的右边， 又或者就是等于这个数。 那么排序的目的就是给我们定下了这么个参照 ”规则“ ，小伙伴们可以仔细想想这个道理。
我们用数学公式来描述这个过程：

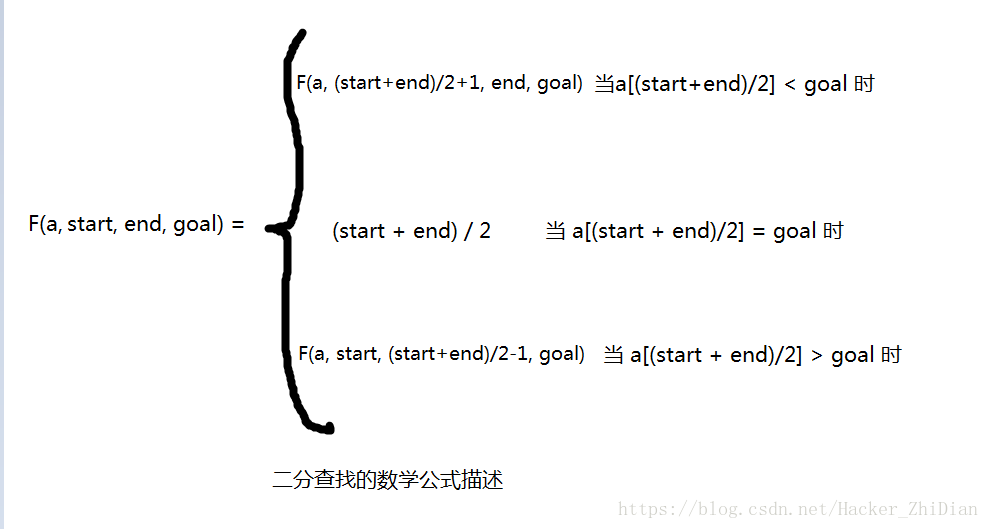
下面给出二分查找的C语言实现代码：

#include 

// 在升序数组 a 中查找 goal 的位置，
// 如果未找到，返回 -1 ,n 为数组长度 
int binary_search(int a[], int n, int goal) {
	int left = 0, right = n-1, mid;
	while (left <= right) {
		// 这里为了防止数值越界没有采用 (left + right) / 2 的方法
		mid = left + (right - left) / 2;
		if (a[mid] < goal) {
			left = mid + 1;
		} else if (a[mid] > goal) {
		 	right = mid - 1;
		} else {
			return mid;
		}
	}
	return -1;
}

int main() {
	int a[] = {1, 2, 3, 4, 4};
	printf("%d", binary_search(a, 5, 2));
	
	return 0;
}

课后对话

老师：假设世界人口总数为 100 亿，那么给所有人进行编号需要多少位二进制数？ 学生：10 位有 1024 人...... 嗯， 300 位左右吧？ 老师：不，34 位就足够了 学生：这就够了吗？ 老师：即使给宇宙中所有原子编号，也不需要 300 位哦！

第八章 ：不可解问题

反证法

同数学归纳法一样，反证法也是一种数学上的证明方法，对于一个要证明的结论，有些时候我们从正面可能难以下手，这时候我们可以考虑利用反证法从反面证明。反证法有两个步骤：

1、首先假设一个命题 Q 为要证明命题的否定形式；
2、根据第一步做出的假设进行推导，推出与命题 Q 矛盾的结果。

我们来看个例子，证明：不存在最大的整数。
这个是典型的利用反证法的例子，我们假设命题 Q 为 “存在最大的整数，并且命名为 M”，那么 M+1 就比 M 大，这与假设的命题 Q 中 “M 是最大的整数相矛盾”。因此假设错误，原命题成立，即不存在最大的整数。

再来看一个例子：证明质数是无穷的。
先做出假设命题 Q：质数是有穷的，那么所有的质数集合就可以写成：2、3、5、7、…、P。
现在，将所有的质数相乘 + 1 的结果记为 X（即令 X = 2*3*5*7*......*P + 1），那么我们知道，X 肯定比 P 大，也就是说 X 不是质数，另外， X 本身除以 2、3、5、7、…、P 中的任何一个数余数都为 1 （X 为所有质数的乘积 + 1），所以根据质数的定义，X 只能被 1 和 X 本身整除，于是 X 是质数，这与刚刚推理出来的 X 不是质数相矛盾，于是假设的命题 Q 是错误的，原命题成立，即质数是无穷的。

不可解问题

不可解问题是 `原则上不能用程序来解决的问题`。也就是不包含在 `程序可解问题集合` 中的问题。 程序是为了解决一系列特定问题而产生的工具，但是依然存在某些通过程序也解决不了的问题，来看几个例子：

哥德巴赫猜想：任意一个大于 3 的偶数都可以写成两个质数之和。
通过程序，我们可以判断哥德巴赫猜想对于某一个大于 3 的偶数是否成立，但是不是全部，因为程序能判断的数据总是有限的，而不是无穷的，不管计算机的储存容量多大，其能储存的数据肯定是有限的，所以我们无法通过计算机程序来证明哥德巴赫猜想，只能对某一些特定的数字来判断其是否符合哥德巴赫猜想。

总结

本文总结自 《程序员的数学》 一书，对其中的内容作了一个小概括，对于某些例子和问题做了点细微的修改，并且加入一些自己的理解。
如果博客中有什么不正确的地方，还请多多指点，如果觉得本文对您有帮助，请不要吝啬您的赞。

谢谢观看。。。。