数据结构复习之顺序表以及链表的方式实现常用的几种排序算法
文章目录
- 如何选择
- 综述
- 完整代码-顺序表版本
- 堆排序(小顶堆增量求topk-海量数据排序)
- 完整代码-链表版本
- 冒泡排序
- 快速排序
- 插入排序
- 直接插入排序
- 希尔排序
- 折半插入排序
- 选择排序
- 直接(简单)选择排序
- 堆排序
- 归并排序
- 基数排序
- 总结
- 参考
先提两个问题:
- 插入排序为什么比冒泡常用?
(两者的最优、平均、最差时间复杂度都相同,且都是原地排序——时间复杂度O(1),并且都是)
因为冒泡排序的赋值交换次数比插入排序多(插入排序每次交换只需要一次赋值)
- 归并的最差时间复杂度比快排低,但是为什么比快排应用更广泛
因为(没想好)
如何选择
- 折半查找:记录数较多(但不是海量,数据不分布均匀)
- 桶排序:数据海量,全量排序,数据分布均匀
- 快速排序:就平均时间而言,快排是所有排序算法中效果最好的
- 堆排序:数据多,求TopN的场景
- 基数排序:数据多,全量排序,但是数据的范围小,数据可以不均匀(比如高考分数排序)【计数排序也行,但是计数排序处理小数或负数需要扩大范围】
【再者,比如对100万个手机号码做排序,使用计数排序就不好,使用快排也不好。这时候使用基数排序或者桶排序更佳】
使用基数排序时,如果数字(或字符串)不等长怎么办?
在后面补0 - 直接插入:数据较少,或者数据基本有序
- 若n较小(如n≤50),可采用直接插入或直接选择排序
- 若n较大,则应采用时间复杂度为O(nlgn)的排序方法:快速排序、堆排序或归并排序
快排、冒泡、插入、shell排序,会受到初始序列的影响。
综述
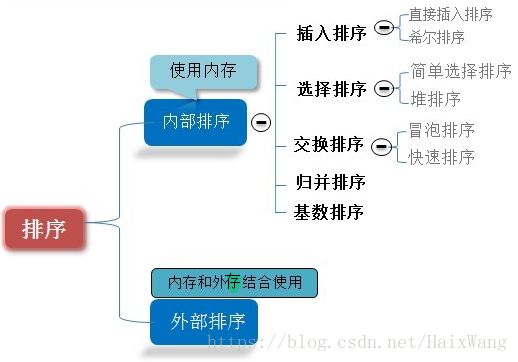
排序大的分类可以分为两种:内排序和外排序。
内排序是指所有的数据已经读入内存,在内存中进行排序的算法。排序过程中不需要对磁盘进行读写。同时,内排序也一般假定所有用到的辅助空间也可以直接存在于内存中。
外排序即内存中无法保存全部数据,需要进行磁盘访问,每次读入部分数据到内存进行排序。
完整代码-顺序表版本
package list;
import java.util.Arrays;
/**
* Descirption:分别用顺序表以及链表的方式实现常用的几种排序算法
*
* @author 王海
* @version V1.0
* @package list
* @date 2018/4/7 16:25
* @since 1.0
*/
public class MultiSortArrayAndList {
private static final float[] FORSORT = {10, -2, 3, -1111111111.9999999f, 55, 32.8f, 66, 7.8f, 10233.88f, 52222, 45.67f, 13, 654, 99999, 1000000.666f, 77.77f, 3214, 66, 736.2f, 5, 23, 65465, 54783, 9999.999f, 5664645, -33, -66.5566778899f, 2147483647.555f, 2147483647};
/**
* 冒泡排序,带标志位(属于交换排序)
*
* @param forSort 等待排序的序列
*/
private void bubbleSort(float[] forSort) {
String name = "冒泡";
long begin = System.nanoTime();
if (forSort.length <= 1) {
printHelper(name, forSort, begin);
return;
}
// 冒泡排序
for (int i = 0; i < forSort.length - 1; i++) {
// 假设下一次不需要再排序
boolean sorted = false;
for (int j = 0; j < forSort.length - i - 1; j++) {
// 这里-i是因为前几次的排序已经沉底了i个数
if (forSort[j] > forSort[j + 1]) {
float temp = forSort[j];
forSort[j] = forSort[j + 1];
forSort[j + 1] = temp;
// 排序过了
sorted = true;
}
}
if (!sorted) {
break;
}
}
printHelper(name, forSort, begin);
}
/**
* 快速排序(属于交换排序)
*
* @param forSort 等待排序的序列
* @param left 左
* @param right 右
*/
private float[] quickSort(float[] forSort, int left, int right) {
if (forSort.length <= 1) return;
int i = left;
int j = right;
// 递归的结束条件
if (left < right) {
float benchmark = forSort[left];
// 下面不能写if,因为并不是说左右指针各移动一次就能保证左右指针“碰头”;完成一次排序
while (i < j) {
// 右侧比较,小则往前放,大则右指针继续“向左前进”
while (i < j && forSort[j] > benchmark) {
--j;
}
// while循环退出,如果left还小于right,就该交换数据了
if (i < j) {
forSort[i++] = forSort[j];
}
// 左侧比较,大则往后放,小则指针继续“向右前进”
while (i < j && forSort[i] < benchmark) {
++i;
}
if (i < j) {
forSort[j--] = forSort[i];
}
}
forSort[i] = benchmark;
// 左部分递归
quickSort(forSort, left, i - 1);
// 右部分递归(编译器是用栈实现递归,之前的i的状态会“回来”)
quickSort(forSort, i + 1, right);
}
return forSort;
}
/**
* 直接排序(属于插入类排序)
*
* @param forSort 等待排序的序列
*/
private void driectSort(float[] forSort) {
String name = "直接插入";
long begin = System.nanoTime();
if (forSort.length <= 1) {
printHelper(name, forSort, begin);
return;
}
for (int i = 1; i < forSort.length; i++) {
// 注意,tmp是“准备”本次排序的那个数
float temp = forSort[i];
// 第一次j为0,因为第一个数有序
int j = i - 1;
while (j >= 0 && temp < forSort[j]) {
// 大的先后移
forSort[j + 1] = forSort[j];
// 没必要马上将当下就位置处的值设为temp,小的继续“往前”
--j;
}
// j已经小于0了,记得加回去
forSort[++j] = temp;
}
printHelper(name, forSort, begin);
}
private void shellSort(float[] forSort) {
String name = "希尔";
long begin = System.nanoTime();
if (forSort.length <= 1) {
printHelper(name, forSort, begin);
return;
}
// 初始增量increment为length / 2【上下取整都行】
// 向上取整用Math.ceil()
// 向下取整用Math.floor(),int a = b/c为下取整
int incrementNum = forSort.length / 2;
while (incrementNum >= 1) {
// 这里的i < forSort.length还不太规范,有多余
for (int i = 0; i < forSort.length; i++) {
// 进行直接插入排序
for (int j = i; j < forSort.length - incrementNum; j = j + incrementNum) {
int drict = j;
// 注意,tmp是“准备”本次排序的那个数
float tmp = forSort[drict + incrementNum];
while (drict >= 0 && forSort[drict] > forSort[drict + incrementNum]) {
forSort[drict + incrementNum] = forSort[drict];
drict -= incrementNum;
}
forSort[drict + incrementNum] = tmp;
}
}
//设置新的增量
incrementNum = incrementNum / 2;
}
printHelper(name, forSort, begin);
}
private void binaryInsertSort(float[] forSort) {
String name = "折半插入";
long begin = System.nanoTime();
if (forSort.length <= 1) {
printHelper(name, forSort, begin);
return;
}
int n = forSort.length;
int i, j;
// "本次"插入数据时,前面已有i个数
for (i = 1; i < n; i++) {
// temp为本次循环待插入有序列表中的数
float tmp = forSort[i];
int low = 0;
int high = i - 1;
// while循环,找到temp插入有序列表的正确位置
while (low <= high) {
// 有序数组的中间坐标,此时用于二分查找,减少查找次数
int mid = (low + high) / 2;
if (forSort[mid] = tmp) {
low = mid;
break;
}
// 若有序数组的中间元素大于待排序元素,则有序序列向中间元素之前搜索,否则向后搜索
if (forSort[mid] > tmp) {
high = mid - 1;
} else {
low = mid + 1;
}
}
for (j = i; j > low; ) {
// 从最后一个元素开始,前面的元素依次后移
forSort[j] = forSort[--j];
}
// 插入temp
forSort[low] = tmp;
}
printHelper(name, forSort, begin);
}
/**
* 通用打印方法打印
*
* @param sorted 排序好的数组
* @param sortName 排序方法
* @param beginTime 排序开始时间
*/
private void printHelper(String sortName, float[] sorted, long beginTime) {
System.out.println("\n" + sortName + ", 排序耗时=======" + (System.nanoTime() - beginTime) + "纳秒");
for (float value : sorted) {
System.out.print(value + " ");
}
}
public static void main(String[] args) {
for (float aCopy : FORSORT) System.out.print(aCopy + ", ");
MultiSortArrayAndList msort = new MultiSortArrayAndList();
/* 数据量小,比较不出时间 */
// 冒泡排序
msort.bubbleSort(Arrays.copyOf(FORSORT, FORSORT.length));
// 快速排序
long begin = System.nanoTime();
float[] sorted = msort.quickSort(Arrays.copyOf(FORSORT, FORSORT.length), 0, FORSORT.length - 1);
System.out.println("\n快速排序, 耗时=======" + (System.nanoTime() - begin) + "纳秒");
for (float value : sorted) {
System.out.print(value + " ");
}
// 直接插入
msort.driectSort(Arrays.copyOf(FORSORT, FORSORT.length));
// 希尔排序
msort.shellSort(Arrays.copyOf(FORSORT, FORSORT.length));
// 折半查找排序
msort.binaryInsertSort(Arrays.copyOf(FORSORT, FORSORT.length));
}
}
堆排序(小顶堆增量求topk-海量数据排序)
package priactice;
import java.util.Arrays;
/**
* package: priactice
*
* descirption:
*
* @author 王海
* @version V1.0
* @since
2018/9/2 20:01
*/
public class HeapSortSmall {
/**
* 构建小顶堆(size=10)
*/
public static void adjustHeap(int[] a, int i, int len) {
int temp, j;
temp = a[i];
for (j = 2 * i + 1; j < len; j = j * 2 + 1) {
if (j + 1 < len && a[j] > a[j + 1])
++j; // j为较小儿子的下标
if (temp <= a[j])
break;
a[i] = a[j];
i = j;
}
a[i] = temp;
}
public static void heapSort(int[] a) {
// 初始化小顶堆
int i;
// 最后一个非叶子节点开始(将其左儿子和右儿子比较)
for (i = a.length / 2 - 1; i >= 0; i--) {
adjustHeap(a, i, a.length);
}
/**
* 全部读入内存的版本
*/
// for (i = a.length - 1; i > 0; i--) {// 将堆顶记录和当前未经排序子序列的最后一个记录交换
// int temp = a[0];
// a[0] = a[i];
// a[i] = temp;
// adjustHeap(a, 0, i);// 将a中前i个数重新调整为小顶堆
// }
/**
* TOP10版本
*/
int[] ex = {100, 5, 210, 150};
for (int val : ex) {
if (val > a[0]) {
a[0] = val;
adjustHeap(a, 0, a.length);
}
}
//降序
for (i = a.length - 1; i > 0; i--) {// 将堆顶记录和当前未经排序子序列的最后一个记录交换
int temp = a[0];
a[0] = a[i];
a[i] = temp;
adjustHeap(a, 0, i);// 将a中前i个数重新调整为小顶堆
}
}
public static void main(String[] args) {
int a[] = {90, 40, 60, 50, 20, 70, 80, 40, 30, 10};
heapSort(a);
System.out.println(Arrays.toString(a));
}
}
完整代码-链表版本
TODO
折半查找属于随机访问特性 链表不行
堆排序也不能用链表 因为调整堆时没法随机访问底层孩子节点
快速排序、归并排序、基数排序可用链表
插入排序链表比数组要快一些 减少移动次数
##交换排序
交换类排序的核心是“交换”,每一趟排序,都可能有交换动作。
冒泡排序
1.原理:比较两个相邻的元素,每一次都让值大的元素“下沉”,也就是说冒泡排序每一次比较都会交换数据。
2.时间复杂度:
- 完全正序时,只需要走一趟即可完成排序(添加一个布尔型标志位)
- 完全逆序时,则需要进行n-1趟排序。每趟排序要进行n-i次比较(1≤i≤n-1),且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下,比较和移动次数均达到最大值:冒泡排序的最坏时间复杂度为:O(n2)
3.空间复杂度:
最优的空间复杂度就是开始元素顺序已经排好了,则空间复杂度为:0(不单独使用交换变量的话:a = a + b; b = a - b; a = a - b);
最差的空间复杂度就是所有元素逆序排序,则空间复杂度为:O(n);
平均的空间复杂度为:O(1);
4.思路:需要两层循环,
外层是遍历每个元素,共需要n-1趟循环;
内层是相邻数的比较,每趟比较n-趟数。
快速排序
1.原理:“分而治之”的思想,围绕“中枢”值分为两部分;需要有前后两个指针(或者说引用),选择一个基准元素(通常是开头或者结尾的元素),对齐进行复制;从末端开始扫描,比被复制的数小的话,将其赋予前面的指针;进行一次赋值后,前指针向后移动,当遇到比被复制的值大的值时,将其赋予后面的指针;对于每一趟的结果,复用上面的方法。

2.时间复杂度:
待排序的序列越接近无序,效率越高。
最坏:最坏情况是指每次区间划分的结果都是基准关键字的左边(或右边)序列为空,即选择的关键字是待排序记录的最小值或最大值。最坏情况下快速排序的时间复杂度为O( n 2 n^2 n2)
最好:O(n l o g 2 n log_2{n} log2n)
3.空间复杂度:
快排需要递归的“辅助”,不是原地排序。递归需要用栈,所以空间复杂度会稍微高些:O( l o g 2 n log_2{n} log2n)
插入排序
原序列已经有序,“新来的”需要找准自己的位置。
直接插入排序
1.原理:我们从前往后进行排序,一开始只看第一个元素,肯定是有序的。现在插入第二个,与第一个比较,小的往前;接下来第三个元素与第二个元素比较,若大于之,顺序不变,小于之,继续往前比较,直到找到自己的位置。依次类推。
2.时间复杂度:
- 最好的情况是,每一次输入的顺序都刚好小于前者,这样就只有一层循环真正起作用,那么复杂度就是O(n)
- 最坏的情况是,O( n 2 n^2 n2)
3.空间复杂度:只需要借助一个temp变量,O(1)
4.思路:
只需要借助一个temp变量,有需要改变位置的节点时则用,不需要改变位置则节点“原地不动”。
希尔排序
1.原理:希尔排序又叫“缩小增量排序”。我们将原始序列按照相同比例分为几个不同的子序列,这个“比例”叫做增量。分别对这些子序列进行直接插入排序,增量不断的缩小,直到增量为1,最后综合起来,排序完成。
希尔排序会造成值相同的元素位置颠倒,所以不稳定。
2.平均时间复杂度:O(n l o g 2 n log_2{n} log2n)
3.空间复杂度:O(1)
4.思路:同原理。
折半插入排序
1.原理:折半插入算法是对直接插入排序算法的改进,排序原理同直接插入算法,与直接插入算法的区别在于:在有序表中寻找待排序数据的正确位置时,使用了折半查找/二分查找。
适合于初始比较有序的序列,但是插入时的比较次数与初始序列无关。
2.时间复杂度:
- 最好的情况是,O(n l o g 2 n log_2{n} log2n)
- 最坏的情况是,O(n),退化为单枝树,查找退化为顺序查找,最坏情况变为O(n)。
3.空间复杂度:O(1)
选择排序
每一趟排序都要选出最小(大)的。
直接(简单)选择排序
1.原理:。
2.时间复杂度:
- 最好的情况是,那么复杂度就是O(n)
- 最坏的情况是,O( n 2 n^2 n2)
3.空间复杂度:O(1)
4.思路:
。
堆排序
1.概述:
最终降序,也就是说,要求最大k个数,需要使用小顶堆,当新读入内存的数字大于堆中最小值时,替换掉,重建堆秩序;
求最小k个数,则相反。
2.时间复杂度:
- 最好、平均、最坏都是O(n l o g 2 n log_2{n} log2n)
3.空间复杂度:O(K):k是初始堆的大小。如果内存能装得下,那就是O(n)
4.思路:
归并排序
1.原理:。
2.时间复杂度:
- 最好的情况是,那么复杂度就是O(n)
- 最坏的情况是,O( n 2 n^2 n2)
3.空间复杂度:O(1)
4.思路:
。
基数排序
1.原理:。
2.时间复杂度:
- 最好的情况是,那么复杂度就是O(n)
- 最坏的情况是,O( n 2 n^2 n2)
3.空间复杂度:O(1)
4.思路:
总结
- **平均性能为O(n^2)的有:**直接插入排序,直接选择排序,冒泡排序
在数据规模较小时(9W内),直接插入排序,选择排序差不多。 - **平均性能为O(nlogn)的有:**快速排序,归并排序,堆排序。其中,快排是最好的,其次是归并,堆排序在数据量很大时效果明显(堆排序适合处理大数据)。
- O(n1+£)阶:£是介于0和1之间的常数,即0<£<1。希尔排序
**稳定排序:**插入排序,冒泡排序,二叉树排序,归并排序
不稳定排序:快速排序(快),希尔排序**(些),选择排序(选),堆排序(一堆)**。
【只需记住一句话(快些选一堆美女)是不稳定的,其他都是稳定的,OK轻松搞定。】
选择思路:
因为不同的排序方法适应不同的应用环境和要求,所以选择合适的排序方法应综合考虑下列因素:
①待排序的记录数目n;
②记录的大小(规模);
③关键字的结构及其初始状态;
④对稳定性的要求;
⑤时间和辅助空间复杂度等;
⑥存储结构。
参考
[1] 常见排序算法及对应的时间复杂度和空间复杂度
[2]排序算法性能和使用场景总结
数据结构复习之顺序表以及链表的方式实现常用的几种排序算法
[3] 白话经典算法系列之六 快速排序 快速搞定

