奇异值分解(SVD)小结
目录
阵的简单理解
矩阵作用于向量
用矩阵的表达一个实体
特征值和特征向量
奇异值分解
Hermitian矩阵
共轭转置
酉矩阵
谈谈《数学之美》对SVD的理解
阵的简单理解
矩阵从我的理解来看,可以从两个角度来看。一个是矩阵是作用于向量,一个是矩阵表达一个实体。
矩阵作用于向量
对于线性空间中,对向量的变换就是通过矩阵对向量的作用来实现的,矩阵本身就表示着一种变换。假设目前所讨论的矩阵是非奇异的![]() 阶方阵。对矩阵对向量的变换,可以从两个不同的角度来看:一、从同一个坐标系来看,矩阵对向量的变换就是伸缩或者旋转。二、同一个向量,在不同坐标系下的度量。比如:
阶方阵。对矩阵对向量的变换,可以从两个不同的角度来看:一、从同一个坐标系来看,矩阵对向量的变换就是伸缩或者旋转。二、同一个向量,在不同坐标系下的度量。比如:
![]()
1、从第一个角度来看就是,向量
经过矩阵
的作用变成了向量
,矩阵表示一种运行方式。
2、从第二个角度来看就是,那么矩阵就表示着一个坐标系(因为非奇异,故矩阵
是有
个线性无关的向量组成),
就是在坐标系
下的一个度量结果,只不过这里的矩阵
不一定是单位矩阵,所以坐标轴上度量单位不一定是单位1。而向量
是单位矩阵
所表示的坐标系下的度量结果。即:
由上式可以看的出,一个向量,他在坐标系![]() 中的表示结果是向量
中的表示结果是向量![]() ,它在坐标系
,它在坐标系![]() 中的表示结果是向量
中的表示结果是向量![]() ,这表明什么?向量x和向量b,表示的是同一个向量,只不过是在不同的坐标系下,每个向量的度量结果不一样而已,即表现形式不同,但本质是一个东西。
,这表明什么?向量x和向量b,表示的是同一个向量,只不过是在不同的坐标系下,每个向量的度量结果不一样而已,即表现形式不同,但本质是一个东西。
我们知道一个向量在不同基下的坐标是不一样的,即向量在不同空间的测量结果是不一样的。如果举一个不恰当的例子,比如水,在零度以下是冰,在100度以上是水蒸气,你可以这样理解,水在0度的环境下的表现形式是冰,在100度的环境下的表现形式是水蒸气,他们只不过存在形式不同,但都是![]() 。那么矩阵是不是也可以看成向量所处的环境呢?(我们目前都是假设矩阵是非奇异的),我想是可以的。无论是把矩阵看成是向量所处环境也好,还是看成空间坐标系也好,不可否认的是,矩阵包含着度量的能力,他可以表达一种空间信息,此时矩阵表示一种度量方式。
。那么矩阵是不是也可以看成向量所处的环境呢?(我们目前都是假设矩阵是非奇异的),我想是可以的。无论是把矩阵看成是向量所处环境也好,还是看成空间坐标系也好,不可否认的是,矩阵包含着度量的能力,他可以表达一种空间信息,此时矩阵表示一种度量方式。
由此矩阵作用于向量或者矩阵,可以把矩阵看成是动态的形式。
用矩阵的表达一个实体
一副图像在计算时,它是以一个矩阵的形式表达的;在NLP中,文本与词的关系,也是以矩阵的形式存在的。此时矩阵![]() 表达一个具体的事物,此时矩阵就是一种静态的表示结果。
表达一个具体的事物,此时矩阵就是一种静态的表示结果。
啰里啰嗦了那么多,就是为了加深理解矩阵的意义,矩阵在不同的情况下,其作用是不一样的。
特征值和特征向量
如果![]() 是n阶方阵,如果存在一个非零的常数
是n阶方阵,如果存在一个非零的常数![]() 和一个n维的向量
和一个n维的向量![]() 使得:
使得:![]() ,则称
,则称![]() 是矩阵
是矩阵![]() 的特征值,
的特征值,![]() 就是其对应的特征向量。翻译成白话就是:如果矩阵
就是其对应的特征向量。翻译成白话就是:如果矩阵![]() 使得一个向量伸缩,那么该向量就是矩阵
使得一个向量伸缩,那么该向量就是矩阵![]() 的一个特征向量,伸缩的尺度就是特征值。
的一个特征向量,伸缩的尺度就是特征值。
如果你觉得矩阵表达运动时比较好理解,那么特征向量就是,各个分运动的方向,对应的特征值,就是运动的距离。如果你觉得矩阵作为表达实体时比较好理解,那么特征向量,就是该实体的某一特征,对应的特征值就是该特征的重要程度。
尤其是矩阵表达一个实体时,矩阵的特征分解显得尤为重要,因为此时的矩阵往往是稀疏的,维度比较大的,在存储或者计算时会浪费很多资源,此时特征值和特征向量的作用就显得尤为重要了,我们可以选择几个特征值最大的向量,就可以表达该实体,这样就可以对原来的矩阵起到了很好的降维作用,而且可以消除很多噪声。可以参考这个例子 。
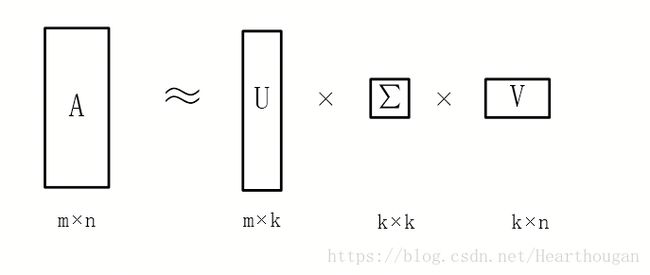
奇异值分解
之前说的方阵都是n阶方阵,那么对于机器学习中很多时候面对的矩阵都是![]() 的,这个时候,我们也想跟方阵一样找出对应的特征值和特征向量,那么有什么方法?答案就是奇异值分解,此时的奇异值就是对应n阶方阵的特征值,只不过此时不再称呼特征值和特征向量了,因为解法不同以及分解出来的矩阵表达的意义也不同。在说奇异值分解之前,先交代两个概念。Hermitian矩阵和酉矩阵。
的,这个时候,我们也想跟方阵一样找出对应的特征值和特征向量,那么有什么方法?答案就是奇异值分解,此时的奇异值就是对应n阶方阵的特征值,只不过此时不再称呼特征值和特征向量了,因为解法不同以及分解出来的矩阵表达的意义也不同。在说奇异值分解之前,先交代两个概念。Hermitian矩阵和酉矩阵。
Hermitian矩阵
如果![]() 阶复方阵
阶复方阵![]() 是对称的,且对称单元互为共轭,即,矩阵
是对称的,且对称单元互为共轭,即,矩阵![]() 的共轭转置矩阵等于它本身,称
的共轭转置矩阵等于它本身,称![]() 为Hermitian矩阵。例如:
为Hermitian矩阵。例如:
共轭转置
矩阵有实数矩阵和复数矩阵。转置矩阵仅仅是将矩阵的行与列对换,而共轭转置矩阵在将行与列对换后还要让每个元素共轭一下。共轭,就是将形如a+bi的数变成a-bi,实数的共轭是它本身。
故,实数矩阵的共轭转置矩阵就是转置矩阵,复数矩阵的共轭转置矩阵就是上面所说的行列互换后每个元素取共轭。
酉矩阵
我们说的正交矩阵是属于![]() 的,是实数域上的。那么推广到复数域:
的,是实数域上的。那么推广到复数域:
假设![]() ,
,![]() 为复数域,若:
为复数域,若:
![]()
则称![]() 就是酉矩阵。
就是酉矩阵。
定理:令
,则存在正交矩阵(或者酉矩阵)
和
,使得:
现在证明这个定理是怎么来的,为了方便理解,先交代几个引理。
引理一、Hermitian矩阵
可酉对角化,且特征值是非负的。
引理二、
。
引理三、
的充要条件是
。
证明:![]()
设![]() ,根据引理一和引理二,可知
,根据引理一和引理二,可知![]() 可以酉对角化,且
可以酉对角化,且![]() ,那么存在一个
,那么存在一个![]() 阶的酉矩阵
阶的酉矩阵![]() 使得:
使得:
即:![]() ,其中
,其中![]() 为
为![]() 的非负特征根。
的非负特征根。
令![]() ,我们把酉矩阵
,我们把酉矩阵![]() 拆分成两个子矩阵
拆分成两个子矩阵![]() 和
和![]() ,有:
,有:
![]()
![]()
易知,![]() ,根据引理三可知
,根据引理三可知![]() 。
。
则有
由于![]() 是对角矩阵,故,
是对角矩阵,故,![]() ,
,![]() 由此可得:
由此可得:
![]()
![]()
![]()
令![]() ,则有:
,则有:![]() 。我们构造一个酉矩阵
。我们构造一个酉矩阵![]() ,使得
,使得![]() ,也就是各向量之间是相互正交的,然拼接成和酉矩阵
,也就是各向量之间是相互正交的,然拼接成和酉矩阵![]() 同等规模的酉矩阵
同等规模的酉矩阵![]() 。
。
则![]() ,证毕。
,证毕。
我们对酉矩阵![]() 进行奇异值分解,同理可以得出:
进行奇异值分解,同理可以得出:
![]()
我们已经知道对![]() 的奇异值分解为:
的奇异值分解为:
![]()
如果矩阵
的秩是
,则有:
酉矩阵
的前
列组成矩阵
的列空间的标准正交基。
酉矩阵
的前
列组成矩阵
的行空间(或者
的列空间)的标准正交基。
U的后
列组成矩阵
的零空间的标准正交基。
的后
列组成矩阵A的零空间的标准正交基。
我们之前说过,奇异值分解,就是为了找到最重要的特征,用这些特征来表示原来的矩阵,这样可以起到降维的作用,也可以起到消除噪声的作用。那么,当矩阵![]() 的秩
的秩![]() 时,由于奇异值
时,由于奇异值![]() ,因此矩阵
,因此矩阵![]() 的奇异值分解就可以写成:
的奇异值分解就可以写成:
![]()
这种情况就称为矩阵![]() 的截尾奇异值分解。
的截尾奇异值分解。
但是大多数的时候,有些奇异值不为0对应的特征向量我们也会舍弃,只会选取以少部分,就是大家常说的前10%甚至1%的奇异值会占总的奇异值的99%。如下图所示:
谈谈《数学之美》对SVD的理解
首先说明一下,吴军老师在数学之美讲解SVD的时候,有点是描述错误的,可能版本比较老,新版不知是否已经更正。在这里叙述时,会更正。
假如对新闻进行分类,把词和文本放到一个矩阵中,可以利用余弦定理来计算相似性;还可以利用对矩阵直接进行SVD分解一次解决。
矩阵![]() 描述了词和文章的关联性,每一行代表一个词,每一列代表一篇文章,如果有
描述了词和文章的关联性,每一行代表一个词,每一列代表一篇文章,如果有![]() 个词,
个词,![]() 篇文章,那么对应的矩阵如下:
篇文章,那么对应的矩阵如下:
其中第![]() 行第
行第![]() 列的元素
列的元素![]() 表示,字典中第
表示,字典中第![]() 个单词出现在第
个单词出现在第![]() 篇文章中的加权词频(如TF-IDF),那么被分解的三个小矩阵:
篇文章中的加权词频(如TF-IDF),那么被分解的三个小矩阵:
- 第一个矩阵
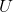 ,表示对词进行分类的一个结果。矩阵
,表示对词进行分类的一个结果。矩阵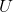 是
是 的特征向量组成的矩阵,
的特征向量组成的矩阵, 是
是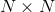 的,词
的,词 词的,表示的就是词与词之间的关系。
词的,表示的就是词与词之间的关系。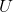 是
是 的一个基,它可以表示词与词之间的空间分布,也就是语义相近与否,所以我们分解出来的第一个矩阵
的一个基,它可以表示词与词之间的空间分布,也就是语义相近与否,所以我们分解出来的第一个矩阵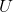 就是对词进行的分类结果。它的每一行表示一个词,每一列表示一个语义相近的词类。每个非零元素表述该词在相应语义中的相关性(重要性),数值越大越相关。
就是对词进行的分类结果。它的每一行表示一个词,每一列表示一个语义相近的词类。每个非零元素表述该词在相应语义中的相关性(重要性),数值越大越相关。 - 最后一个矩阵
 ,表示是对文本的一个分类结果。矩阵
,表示是对文本的一个分类结果。矩阵 是
是 的特征向量组成的空间,
的特征向量组成的空间, 是
是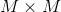 的,文章
的,文章 文章,表示的是文章与文章之间的关系,它的每一列表示一篇文章,每一行表示一个主题,这一列中的每个元素表示在不同主题中的相关性。
文章,表示的是文章与文章之间的关系,它的每一列表示一篇文章,每一行表示一个主题,这一列中的每个元素表示在不同主题中的相关性。 - 第二个矩阵,表示词的语义类和文章的主题之间的关系。如下面这个矩阵:
在矩阵![]() 中,每一行表示一个语义,每一列表示一个主题。每一行的每个元素,表示该语义与主题之间的关系。0.7表示第一个语义与第一个主题相关,0.21表示第一个语义与第二个主题不相关。同理,0.18表示第二个语义与第一个主题不相关,0.63表示第二个语义与第二个主题相关。
中,每一行表示一个语义,每一列表示一个主题。每一行的每个元素,表示该语义与主题之间的关系。0.7表示第一个语义与第一个主题相关,0.21表示第一个语义与第二个主题不相关。同理,0.18表示第二个语义与第一个主题不相关,0.63表示第二个语义与第二个主题相关。
到此SVD讲解完成,从理论到实际的物理意义,花了近两天的复习和总结,啰里啰嗦了这么多,也不知道是否阐述的明白。如有错误,欢迎指正。
参考:
《理解矩阵》孟岩
《数学之美》吴军
《矩阵分析》张贤达