初探最短路径

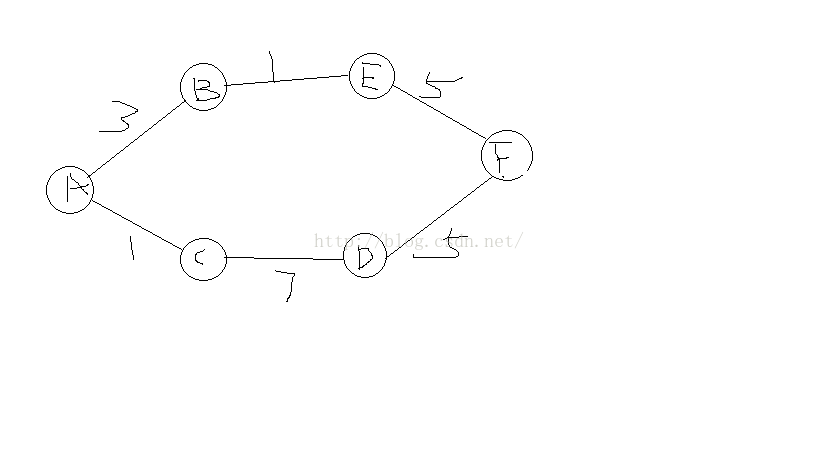
最近有点懵逼，连一个迪杰斯特拉算法都有点云里雾里的样子，钻了个牛角尖，一直弄不懂一个问题，如下图

刚开始我想啊，那个dijkstra算法用了贪心策略，每次都选最短的边，然后我就纳闷了，如果像上面这个图那样不就选错了？

事实证明，是我没有读懂代码，忽略了一个重要且基本的信息，在n个点中，除去原点，他一共计算了n-1次，就是把每个点都计算到了，这样就会实时更新最短路径

#include 
#include 
#include 
using namespace std;
const int V = 9; //定义顶点个数

//从未包含在SPT的集合T中，选取一个到S集合的最短距离的顶点。
int getMinIndex(int dist[V], bool sptSet[V]) {
	   int min = INT_MAX, min_index;
	   for (int v = 0; v < V; v++)
	     if (sptSet[v] == false && dist[v] < min)
	         min = dist[v], min_index = v;
	   return min_index;
}

// 打印结果
void printSolution(int dist[], int n) {
	printf("Vertex   Distance from Source\n");
	for (int i = 0; i < V; i++)
		printf("%d \t\t %d\n", i, dist[i]);
}

//source 代表源点
void dijkstra(int graph[V][V], int source) {
	int dist[V];     // 存储结果，从源点到 i的距离

	bool sptSet[V]; // sptSet[i]=true 如果顶点i包含在SPT中

	// 初始化. 0代表不可达
	for (int i = 0; i < V; i++){
		dist[i] = (graph[source][i] == 0 ? INT_MAX:graph[source][i]);
		sptSet[i] = false;
	}

	// 源点，距离总是为0. 并加入SPT
	dist[source] = 0;
	sptSet[source] = true;

	// 迭代V-1次，因此不用计算源点了，还剩下V-1个需要计算的顶点。
	for (int count = 0; count < V - 1; count++) {
		// u，是T集合中，到S集合距离最小的点
		int u = getMinIndex(dist, sptSet);

		// 加入SPT中
		sptSet[u] = true;

		//更新到V的距离。可以理解为Bellman-Ford中的松弛操作
		for (int v = 0; v < V; v++)
			if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX
					&& dist[u] + graph[u][v] < dist[v])
				dist[v] = dist[u] + graph[u][v];
	}

	printSolution(dist, V);
}

int main() {
	/* 以例子中的图为例 */
	int graph[V][V] =
			{ { 0, 4, 0, 0, 0, 0, 0, 8, 0 }, { 4, 0, 8, 0, 0, 0, 0, 11, 0 }, {
					0, 8, 0, 7, 0, 4, 0, 0, 2 }, { 0, 0, 7, 0, 9, 14, 0, 0, 0 },
					{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
					{ 0, 0, 4, 0, 10, 0, 2, 0, 0 },
					{ 0, 0, 0, 14, 0, 2, 0, 1, 6 },
					{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
					{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };

	dijkstra(graph, 0);

	return 0;
}

代码出处：传送门

这样一看，这种算法好像也就不太完美了

+++++++++++++++++++++++++++++++++++++++分界线+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

接着我又看到了个有向无环图求解最短路径的问题

代码如下：

#include
#include 
#include 
#include 
#define INF INT_MAX
using namespace std;

// 邻接表节点
class AdjListNode
{
    int v;
    int weight;
public:
    AdjListNode(int _v, int _w)  { v = _v;  weight = _w;}
    int getV()       {  return v;  }
    int getWeight()  {  return weight; }
};

// 图
class Graph
{
    int V;    // 顶点个数

    list *adj;

    void topologicalSortRecall(int v, bool visited[], stack &stk);
public:
    Graph(int V);

    void addEdge(int u, int v, int weight);

    void shortestPath(int s);
};

Graph::Graph(int V)
{
    this->V = V;
    adj = new list[V];
}

void Graph::addEdge(int u, int v, int weight)
{
    AdjListNode node(v, weight);
    adj[u].push_back(node);
}

// 拓扑排序，递归调用。详细解释参考这里：
void Graph::topologicalSortRecall(int v, bool visited[], stack &stk)
{
    // 标记当前节点是访问过的
    visited[v] = true;

    list::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
    {
        AdjListNode node = *i;
        if (!visited[node.getV()])
            topologicalSortRecall(node.getV(), visited, stk);
    }
    stk.push(v);
}

// 从给定的源点s 找出到其它顶点的最短距离.
void Graph::shortestPath(int s)
{
    stack stk;
    int dist[V];

    //标记所有顶点为未访问过的
    bool *visited = new bool[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;

    // 拓扑排序，结果存入stk中
    for (int i = 0; i < V; i++)
        if (visited[i] == false)
            topologicalSortRecall(i, visited, stk);

    // 初始化距离
    for (int i = 0; i < V; i++)
        dist[i] = INF;
    dist[s] = 0;

    // 按照拓扑排序的顺序处理 各个顶点
    while (stk.empty() == false)
    {
        // 获得拓扑排序的下一个顶点
        int u = stk.top();
        stk.pop();

        // 更新所有相邻的顶点
        list::iterator i;
        if (dist[u] != INF)
        {
          for (i = adj[u].begin(); i != adj[u].end(); ++i)
             if (dist[i->getV()] > dist[u] + i->getWeight())
                dist[i->getV()] = dist[u] + i->getWeight();
        }
    }

    // 打印结果
    for (int i = 0; i < V; i++)
        (dist[i] == INF)? cout << "INF ": cout << dist[i] << " ";
}

// 测试
int main()
{

    Graph g(6);
    g.addEdge(0, 1, 5);
    g.addEdge(0, 2, 3);
    g.addEdge(1, 3, 6);
    g.addEdge(1, 2, 2);
    g.addEdge(2, 4, 4);
    g.addEdge(2, 5, 2);
    g.addEdge(2, 3, 7);
    g.addEdge(3, 4, -1);
    g.addEdge(4, 5, -2);
    int s = 1;
    cout << "Following are shortest distances from source " << s <<" \n";
    g.shortestPath(s);

    return 0;
}

这个问题突出的有向无环（这TM不是说废话吗，好吧，强行凑字数中）

留下个问题：有向五环图为什么可以用到了拓扑排序，目前来说如果我遇到这种问题，没有看到上面的代码的话，完全不知道怎么搞
附上一个用两种方法计算：传送门

最近切身体会到懂和知道的区别！！