T1:谁拿了最多奖学金
考察知识：模拟，条件语句
算法难度：X 实现难度：X+
分析：初学者都能做，只要细心把所有条件都考虑完就可以了。
算法流程：
1.读入n
2.循环n次，一边读入数据一边判断可以得那些奖学金，并按题目要求处理
代码：
#include
#include
char top_stu[25],name[25],ldr[5],west[5];
int sum,max_mon,mon,n,score1,score2,paper;
int main(){
scanf("%d",&n);
while(n--){
mon=0;
scanf("%s%d%d%s%s%d",name,&score1,&score2,ldr,west,&paper);
if(score1>80&&paper>0) mon+=8000;
if(score1>85&&score2>80) mon+=4000;
if(score1>90) mon+=2000;
if(score1>85&&west[0]=='Y') mon+=1000;
if(score2>80&&ldr[0]=='Y') mon+=850;
sum+=mon;
if(mon>max_mon) max_mon=mon,strcpy(top_stu,name);
}
printf("%s\n%d\n%d\n",top_stu,max_mon,sum);
return 0;
}
T2:过河
考察知识：动态规划，条件的处理，数学
算法难度：XXX 实现难度：XX+
分析：不看数据范围，这就是一道裸的动态规划题，但是数据特殊L可以很大，M最大值却很小，这就需要我们分析。
先将动态规划：
状态方程：f(i)表示从起点到i点踩到的最少石头数
状态转移：
方程下面那个加一表示坐标i上有石头
时间复杂度：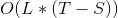
，显然暴力方法会超时
优化：当S!=T时如果两块石头距离相差超过100直接把距离看成100
原理：为什么S!=T时可以这样做呢？
解（xia）释（gao）:
设X,Y是两块相邻石头的坐标且Y-X>=100
考虑X是否可以到Y，不妨设S=T-1
1*.当S!=1时，显然有S,T互质
则aS+bT(a,b为自然数)不能表示的最大整数为(S-1)(T-1)，所以Y-X>=(S-1)*(T-1)时可以保证从X可以到达Y，也可以跳过Y
由于T<=10,显然100满足条件
再考虑S!=T-1则S
2*.S=1
先走Y-X-1步，到达Y-1此时青蛙可以跳过Y,也可以到达Y,满足要求
由解释可以看到，其实100并不是最小的满足要求的数，但是已经完全可以满足时间复杂度了
反思：（第一次AC在几个月前）第二次提交0分全部RE，我当时就震惊了，经过检查我没有把输入的数据排序，然后我又看了一遍原题，它并没有说数据不一定递增啊，而且样例数据还是递增的,那么有迷惑性。我又看了第一次的做题记录第一次也是0分，也是没有排序，这样的教训我居然忘了？！如果你没有排序很可能就只有20分了（然而我不小心把那20分也丢了），所以不管题目说没有最好都要排序，也就是：增强程序的鲁棒性很重要！
代码：
#include
#include
#define Min(var1,var2) (var1>var2?(var2):(var1))
int m,l,s,t;
int mp_pos[105],pos[105],f[10105],np=1;
int main(){
scanf("%d%d%d%d",&l,&s,&t,&m);
for(int i=1;i<=m;i++) scanf("%d",pos+i);
std::sort(pos+1,pos+m+1);
for(int i=1;i<=m;i++){
if(pos[i]-pos[i-1]>=100) mp_pos[i]=mp_pos[i-1]+100;
else mp_pos[i]=mp_pos[i-1]+(pos[i]-pos[i-1]);
}
if(s==t){//处理特殊情况
int cnt=0;
for(int i=1;i<=m;i++) if(pos[i]%s==0) cnt++;
printf("%d\n",cnt);return 0;
}
int RG=mp_pos[m]+1;
for(int i=1;i<=RG+100;i++){
f[i]=105;
for(int k=s;k<=t;k++) if(i>=k)
f[i]=Min(f[i],f[i-k]);
if(mp_pos[np]==i) f[i]++,np++;
}
int ans=105;
for(int i=RG;i<=RG+100;i++) ans=Min(ans,f[i]);
printf("%d\n",ans);
return 0;
}
T3:篝火晚会
没有读懂题目（T_T）。。。 。。。
T4:等价表达式
考察知识：字符串处理，模拟
算法难度：XXX+ 实现难度：XXXX
分析：第一眼看完这道题我想大多数人都是想模拟多项式运算，但仔细想想，我们可以用赋值法计算
我们赋给a一个具体的值并判断多项式运算后的值是否相等来判断两个多项式是否相等。
不过这种方法会不会准确性不够呢？会，如果你只赋一个值。
但是我们可以证明对于两个不完全相等的一元多项式，可以它们相等的值不超过两个多项式中最高次幂的值
所以我们多赋几个值就可以保证正确性了。
所以这道题转化为将一个字符串当成多项式运算，我想大家学栈专题的时候都做过类似的题吧。面对这类题，我们只需要用两个栈，一个储存数字，一个储存运算符，再根据运算符的优先级进行运算。
还是建议不要用gets()，还是讨厌的换行问题，在洛谷上（Linux系统）判断换行符应该用 '\r' ，在vijos（Windows系统）上应该用'\n'，为了保险，我们都判断就可以了。
最让我无语的是洛谷的数据居然有括号不匹配的，我当时就震惊了，但是遇到我们直接跳过就可以了。
代码：
#include
#include
#include
#include
#include
using namespace std;
const int MOD=100000007;
#define ll long long
int n,top1,top2;
ll stk1[105];
char stk2[105];
int order(char ch){
switch(ch){//运算符优先级
case ')':return 4;
case '^':return 3;
case '*':return 2;
case '+':return 1;
case '-':return 1;
case '(':return 0;
} return -1;
}
ll calc(ll a,char op,ll b){
switch(op){
case '+':return (a+b+MOD)%MOD;
case '-':return (a-b+MOD)%MOD;
case '*':return a*b%MOD;
} ll ret=1;
while(b--) ret=ret*a%MOD;
return (ret+MOD)%MOD;
}
bool get_line(char* str){//输入+处理字符串
int pos=0,lc=0;
bool Err=false;
char ch=getchar();
while(!isdigit(ch)&&ch!='a'&&ch!='+'&&ch!='-'&&ch!='*'&&ch!='^'&&ch!='('&&ch!=')') ch=getchar();
while(ch!='\n'&&ch!='\r'){
if(ch!=' '){
if(ch=='(') lc++;
if(ch==')') lc--;
if(lc<0) Err=true;
if(ch=='a'&&pos>0&&isdigit(str[pos-1])) str[pos++]='*';
str[pos++]=ch;
} ch=getchar();
} str[pos]='\0';
if(lc||Err) return true;
return false;
}
ll calc_str(char* s,int a_v){//计算字符串
ll a,b;
char op;
top1=top2=0;
for(int i=0;s[i]!='\0';i++){
if(s[i]=='(') stk2[++top2]=s[i];
else if(isdigit(s[i])){
int v=s[i++]-'0';
while(isdigit(s[i])) v=v*10+s[i++]-'0';
stk1[++top1]=v;i--;
}
else if(s[i]=='a') stk1[++top1]=a_v;
else if(s[i]=='^'){
int v=s[++i]-'0';i++;
while(isdigit(s[i])) v=v*10+s[i++]-'0';
i--;
a=stk1[top1--],b=v;
stk1[++top1]=calc(a,'^',b);
}
else if(s[i]==')'){
while(stk2[top2]!='('){
b=stk1[top1--],a=stk1[top1--],op=stk2[top2--];
stk1[++top1]=calc(a,op,b);
}top2--;
}
else{
while(top2&&order(s[i])<=order(stk2[top2])){
b=stk1[top1--],a=stk1[top1--],op=stk2[top2--];
stk1[++top1]=calc(a,op,b);
}stk2[++top2]=s[i];
}
}
while(top2){
b=stk1[top1--],op=stk2[top2--],a=stk1[top1--];
stk1[++top1]=calc(a,op,b);
}
return stk1[top1];
}
int main(){
// freopen("in.in","r",stdin);
char s[150],s1[150];
ll ans[32];
get_line(s);
scanf("%d",&n);//get_line(s1);
for(int i=0;i<=10;i++) ans[i]=calc_str(s,i);
for(int i=0;i
