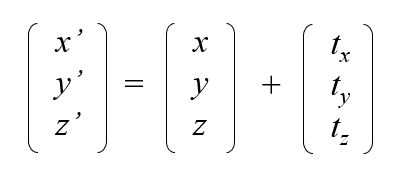3Dslicer中的坐标系统（二）
一、什么是坐标系统
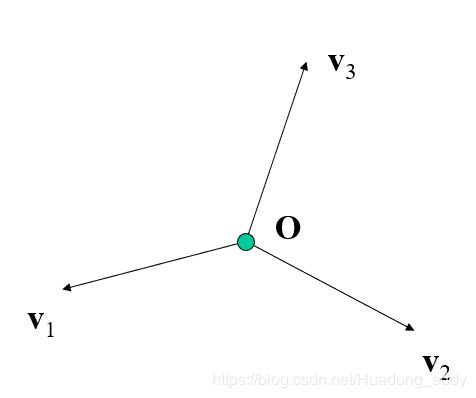
一个三维空间的坐标系统是由一个点O（称为原点）和三个线性无关的三维向量v1, v2, 和 v3组成的。
三维空间坐标系统
线性无关在这里代表任意两个向量之间不平行并且这三个向量不在同一个平面上。
二、RAS坐标系统
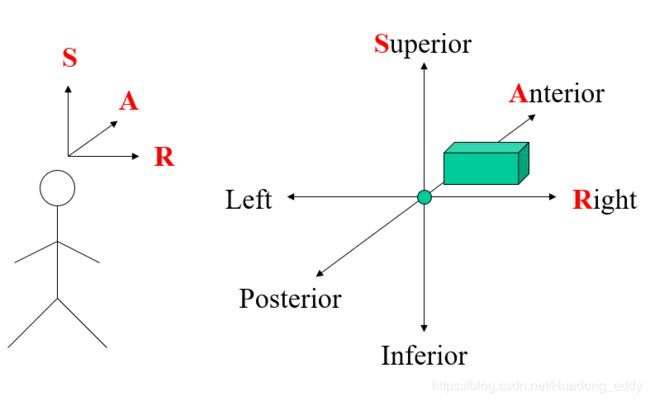
每一个被扫描的物体都有其自身固定的坐标系统称为RAS坐标系统，“RAS” 代表着Right，Anterior，Superior。对于CT和MRI扫描系统来说，RAS坐标系统相对于扫描台和正在扫描的对象或者物体是固定的。（the “scanee” if you wish）
RAS坐标系统示例
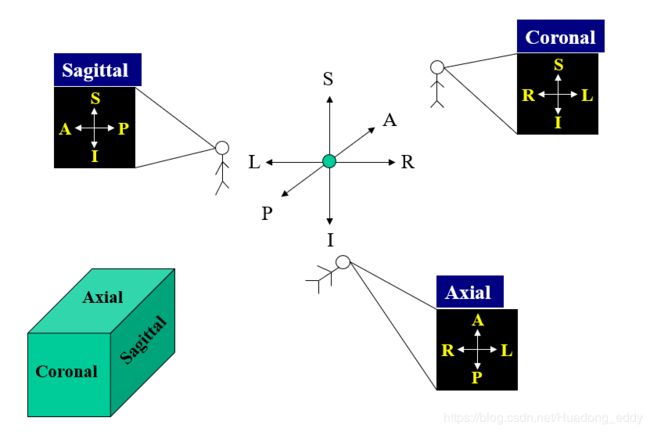
- 三个观察方向（Viewing Directions）
The Three Viewing Directions
- 医学图像扫描方向
医学扫描仪器通过沿着轴来依次扫描单个2D切片来获取整个体数据：
Medical Image Scan Directions
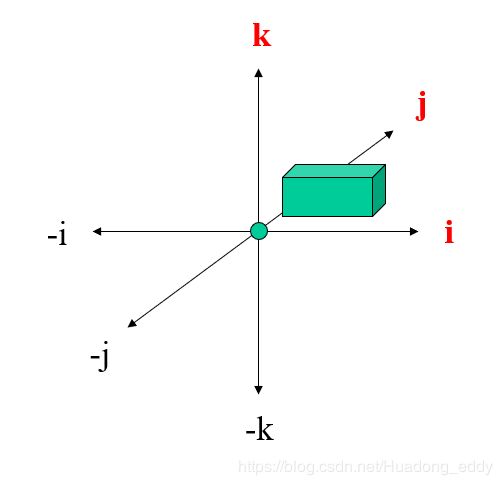
三、IJK坐标系统
每一个医学扫描仪器都有其自己的坐标系统称作IJK坐标系统。IJK坐标系统体现被扫描数据的实际矩形柱，而不是扫描台的位置。(the coordinate system of the “scanner”)
IJK坐标系统
四、坐标系统转换
我们经常需要在不同的坐标系统之间转换，像RAS和IJK坐标系统之间的转换。从一个坐标系统到另一个坐标系统之间的映射是通过一个三维的仿射变换来实现的：由一个错切变换（shear）、一个翻转变换（reflection）、一个旋转变换（rotation）、一个缩放变换（scaling）、和一个平移变换（translation）等一系列基本变换组成。
所谓仿射变换就是一个简单的应用于一个点的矩阵乘法加上一个平移操作。任何仿射变换都可以分解如下形式：
仿射变换形式
五、仿射变换
下面我们来验证一下在三维的标准坐标系统下，一个仿射变换是怎样工作的：这是一个原点在（0，0，0）点，三个基向量为（1，0，0）、（0，1，0）、（0，0，1）的三维坐标系统。我们通常将三个代表基向量的轴标记为X、Y、Z轴。
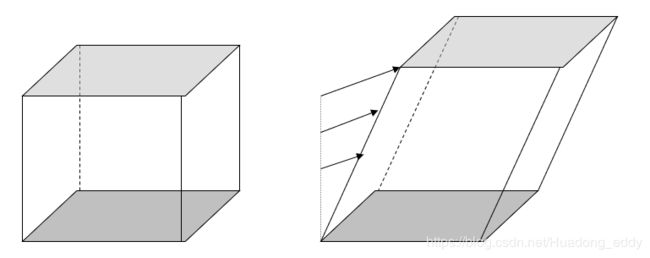
- 错切变换（Shear）：
错切变换可以在三个不同的坐标平面上进行错切：XY, XZ, 和YZ平面。
例如：在XY平面上的错切将会平移图像中每一个平行于XY平面的平面以x和y的量，并且这个量是与平移平面的Z值成比例的。所以Z=0的平面是不用平移的。
错切示意图
在XY平面上的错切：
在XZ平面上的错切：
在YZ平面上的错切：
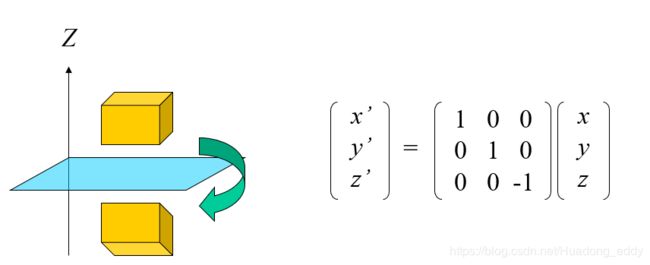
- 翻转变换（Reflection）：
关于XY平面的翻转是一个简单的变换：简单的反向Z坐标。
关于XY平面的翻转
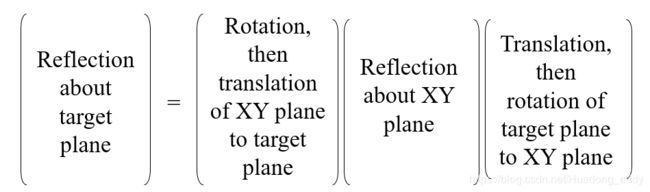
利用上述关于XY平面的翻转我们可以就可以得到关于任何平面的翻转。对于任何仿射变换，关于XY平面的翻转是仅需要的翻转变换，因为关于其它任何平面的翻转我们都可以用关于XY平面的翻转级联上相应的平移和旋转变换来产生（而平移和旋转变换已经被仿射变换所使用）。
关于任何平面的翻转
- 旋转变换（Rotation）
在三维空间中的任何旋转都是绕每个标准坐标轴的旋转的组合。
- 缩放（Scaling）
缩放，也称为扩张，简单地通过Sx、Sy和Sz的因子分别在三个标准坐标方向X、Y和Z的每个方向上拉伸3D空间。
如果Sx = Sy = Sz，缩放被称作各向同性缩放，否则称为各向异性缩放。
- 平移（Translation）
平移是一个非常简单的操作：简单的通过固定的平移向量(tx, ty, tz)来移动空间中的每一个点。
- 仿射变换（Affine Transformations）
我们可以看出，所有仿射变换的组成变换或者是一个3 x 3 矩阵相乘的形式，或者是一个3 x 1 矩阵相加的形式。事实上，所有的由这样一个矩阵相乘跟上这样一个平移组成的变换都是仿射变换。
- 齐次坐标
当使用齐次坐标，我们为所有的点赋予额外的坐标值“1”，为所有的向量赋予额外的坐标“0”。
使用齐次坐标表示形式，所有的仿射变换映射关系都可以用一个矩阵来表示：
- 仿射变换总结：
任何时候你想要将一个坐标系统映射到另一个，你都会使用到仿射变换。
仿射变换在slicer中使用齐次坐标的形式来表示的，即一个4 x 4 的矩阵。
每个仿射变换都由以下箭头中列出的一些（可能不是全部）按顺序应用的组件组成。
