注意meshgrid陷阱！

在matlab命令行窗口输入help meshgrid

[X,Y] = meshgrid(xgv,ygv) replicates the grid vectors xgv and ygv to 
    produce the coordinates of a rectangular grid (X, Y). The grid vector
    xgv is replicated numel(ygv) times to form the columns of X. The grid 
    vector ygv is replicated numel(xgv) times to form the rows of Y.

即创建网格函数将xgv复制n = numel(ygv)次，每一行都是xgv；将ygv复制m = numel(xgv)次，每一列都是ygv。譬如：

xgv = 0:pi/4:pi; 
ygv = 0:1/4:2; 
[X, Y] = meshgrid(xgv, ygv)

结果如下：

X =
         0    0.7854    1.5708    2.3562    3.1416
         0    0.7854    1.5708    2.3562    3.1416
         0    0.7854    1.5708    2.3562    3.1416
         0    0.7854    1.5708    2.3562    3.1416
         0    0.7854    1.5708    2.3562    3.1416
         0    0.7854    1.5708    2.3562    3.1416
         0    0.7854    1.5708    2.3562    3.1416
         0    0.7854    1.5708    2.3562    3.1416
         0    0.7854    1.5708    2.3562    3.1416


Y =
         0         0         0         0         0
    0.2500    0.2500    0.2500    0.2500    0.2500
    0.5000    0.5000    0.5000    0.5000    0.5000
    0.7500    0.7500    0.7500    0.7500    0.7500
    1.0000    1.0000    1.0000    1.0000    1.0000
    1.2500    1.2500    1.2500    1.2500    1.2500
    1.5000    1.5000    1.5000    1.5000    1.5000
    1.7500    1.7500    1.7500    1.7500    1.7500
    2.0000    2.0000    2.0000    2.0000    2.0000

下面要注意了，如果以$(x_i,y_j)$来代表目标网格中的点，比如想要$(x_5,y_3)=(\pi ,0.5)$对于上述已创建的$m\times n$网格，则对应于$X(:,5)$，$Y(3,:)$。
现在考虑要作一三维图$val=(x,y)$，即val随坐标位置不同是变化的，在保持下标不变的情况下，$(\pi ,0.5)$的值应该怎么表示呢？
答案是$X^{\prime }(5,3)$，$Y^{\prime }(5,3)$，但是这样一来，坐标矩阵变成$n\times m$阶，原本为$m\times n$的val也需要倒置才能匹配维度；否则的话，若不倒置而又在保持下标不变，应该这样创建网格：

xgv = 0:pi/4:pi; 
ygv = 0:1/4:2; 
[Y, X] = meshgrid(ygv, xgv)

得到：

Y =
         0    0.2500    0.5000    0.7500    1.0000    1.2500    1.5000    1.7500    2.0000
         0    0.2500    0.5000    0.7500    1.0000    1.2500    1.5000    1.7500    2.0000
         0    0.2500    0.5000    0.7500    1.0000    1.2500    1.5000    1.7500    2.0000
         0    0.2500    0.5000    0.7500    1.0000    1.2500    1.5000    1.7500    2.0000
         0    0.2500    0.5000    0.7500    1.0000    1.2500    1.5000    1.7500    2.0000
         
X =
         0         0         0         0         0         0         0         0         0
    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854
    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708
    2.3562    2.3562    2.3562    2.3562    2.3562    2.3562    2.3562    2.3562    2.3562
    3.1416    3.1416    3.1416    3.1416    3.1416    3.1416    3.1416    3.1416    3.1416

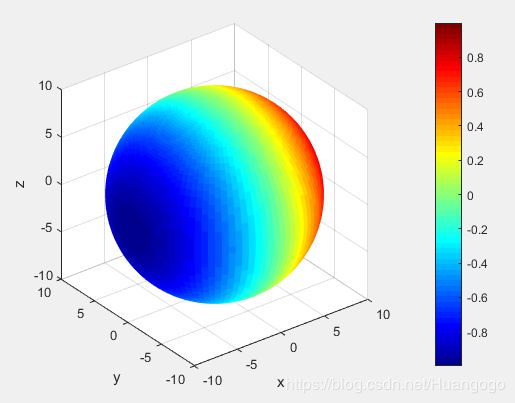
此时可以直接取：$X(5,3)$，$Y(5,3)$组成所需坐标$(\pi ,0.5)$。下面给一个具体作图例子：（这里实际上是四维图，不过第三维r是一个定值，同理）

r = 10;
theta = linspace(0, pi);
phi = linspace(0, 2*pi);
val = rand(100);
for k = 1:100
    val(k,:) = sin(theta) .* cos(phi(k));
end
[el, az] = meshgrid(pi/2 - theta, phi);
% [x,y,z] = sph2cart(azimuth,elevation,r)
[x,y,z] = sph2cart(az,el,r);	% or [x,y,z] = sph2cart(az',el',r'); when using [az, el] = meshgrid(phi, pi/2 - theta);
figure;
s = surf(x,y,z, val);
s.EdgeColor = 'none';
daspect([1 1 1]);
colorbar;
colormap(jet);
xlabel('x'); ylabel('y'); zlabel('z');

正确结果为：

而如果仅将网格语句替换为：

[az, el] = meshgrid(phi, pi/2 - theta);

将得到错误结果：

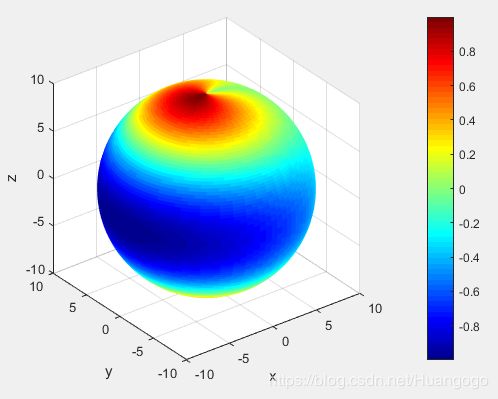
当theta和phi长度不同时会报错，陷阱在于：二者长度相同时程序可以运行，而代码写长了之后，尤其是涉及更多坐标变换的时候，可能就忽略了这一点而花费更多时间排错。